
- •Формулировка основных (6-8) задач эконометрики (на примере)
- •Регрессия: условная вероятность, условная вероятность распределения, свойства условной вероятности двумерной вероятности распределения.
- •Парная и множественная линейные регрессии
- •Определяемая переменная. Определяющие переменные (факторы). Необходимое условия минимума функции нескольких переменных. Мнк.
- •Трендовые модели. Компоненты: тренд, сезонная, циклическая, календарная, инфляционная и стохастическая компоненты.
- •Классическая декомпозиция:
- •Десезонализация:
- •Теория и свойства оценок параметров регрессии: несмещенность, эффективность, состоятельность
- •Условия гаусса-маркова для стохастической компоненты.
- •Понятия гомо- и гетероскедастичности оценок регрессии.
- •Коэффициент детерминации как мера точности моделирования.
- •Оценка точности прогнозирования (понятие рабочей и контрольной выборок).
- •Практически важные модели парных регрессий: линейная, параболическая, обобщенная экспоненциальная, обратная, логистическая.
- •Структуры моделей регрессии: аддитивная, мультипликативная, аддитивно-мультипликативная (смешанная).
- •Дискретизация динамики социально-экономических показателей (теорема котельникова).
- •Модели динамики с распределенными лагами (виды лагов).
- •Методы идентификации койка моделей с распределенными лагами.
- •Метод ш. Алмон для моделей с распределенными лагами.
- •Метод (модель) адаптивных ожиданий для авторегрессионных моделей.
- •Метода (модель) частичной корректировки для авторегрессионных моделей.
- •Фиктивные переменные в эконометрике.
- •Методы экспоненциального и текущего сглаживания.
- •Модель хольта (линейного роста) и хольта-уинтерса.
- •Модель тейла-вейджа.
Понятия гомо- и гетероскедастичности оценок регрессии.
При проведении регрессионного анализа методом наименьших квадратов (МНК) важно учитывать предпосылки этого метода, одной из которых является равенство дисперсий случайных отклонений. Выполнение данной предпосылки называется гомоскедастичностью, невыполнение - гетероскедастичностью.
Скедастичность — относительная вариативность, показанная на диаграмме разброса в строках и столбцах разброса.
Виды
Гомоскедастичность или гомогенность дисперсии — состояние, при котором измерения вариативности колеблются внутри диапазона, ожидаемого при случайной вариативности.
Гетероскедастичность — состояние, при котором измерения вариативности являются большими, чем ожидаемые случайно.
В соответствии с одной из предпосылок МНК нужно, чтобы дисперсия остатков была гомоскедастичной. Это означает, что для каждого значения фактора X остатки е, имеют одну и ту же дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно продемонстрировать на поле корреляции.
Гетероскедастичность (неоднородность) — понятие математической статистики и эконометрии; означает ситуацию, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации метод наименьших квадратов (иначе возможны ошибочные выводы). Гетероскедастичность будет сказываться на уменьшении эффективности оценок.
Гомоскедастичность остатков означает, что для каждого значения фактора xj остатки имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетеродастичности можно наглядно видеть из поля корреляции.
Коэффициент детерминации как мера точности моделирования.
Коэффициент детерминации (R2)— это доля дисперсии отклонений зависимой переменной от её среднего значения, объясняемая рассматриваемой моделью связи (объясняющими переменными). Модель связи обычно задается как явная функция от объясняющих переменных. В частном случае линейной связи R2 является квадратом коэффициента корреляции между зависимой переменной и объясняющими переменными.
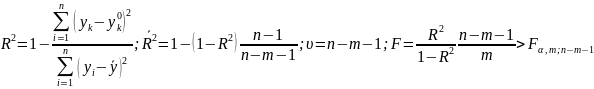
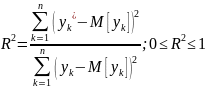
Числитель есть мера остаточного необъяснимого моделью регрессии разброса.
Знаменатель
есть мера общего рассеивания
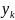 относительно линии
относительно линии
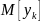 .
.
Характеризует насколько модель дает лучший результат, чем горизонтальная прямая соответствия стационарности показателей.
Оценка точности прогнозирования (понятие рабочей и контрольной выборок).
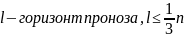
Для
осуществления прогноза выборка делиться
на две части: рабочая
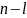 ,
и контрольная
,
и контрольная
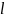 .
.
Рабочая:
строится модель (модифиц), находятся
ее параметры.
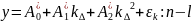
Построив модель, распространим ее на оставшиеся наблюдений.
Если они близки и у нас нет сомнений в инерционности процессов, то и на будущих неизвестных нам значениях будет высокая точность.
Для осуществления прогнозов выборка разбивается на 2 части: рабочая (n-l)- осущ-ся идентификация l и строится модель, находится ее параметр; контрольная (l – наблюдений) – построив модель, распространяем ее на оставшиеся l наблюдений и сравниваем известные l наблюдений с распрост-ми. Если они близки и у нас нет сомнений в инерционности, то и на будущих неизв. Зн-х будет тоже высокая точность.
Характеристики качества прогнозирования
1. Абсолютная ошибка прогноза:
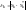 ,
где
,
где
 - фактическое значение показателя на
- фактическое значение показателя на
 -ое
наблюдение;
-ое
наблюдение;
 - прогнозное значение показателя на
- прогнозное значение показателя на
 -ое
наблюдение;
-ое
наблюдение;
2. Средняя абсолютная ошибка прогноза:
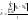 ,
где l
– период упреждения («горизонт»
прогноза);
,
где l
– период упреждения («горизонт»
прогноза);
3. Среднеквадратическая ошибка прогноза и 4. Относительная ошибка прогноза:
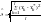 .
.
5.Среднюю относительную ошибку прогноза или MAPE – оценку:
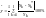 ;
;
6. Коэффициенты несоответствия (коэффициенты Тейла):
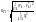
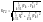 .
.
Адекватность, точность моделирования и прогнозирования модели.
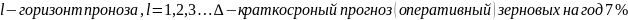
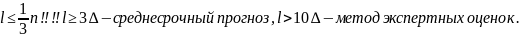
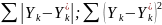
Рисунок!!
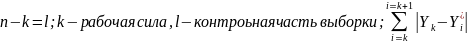
Рисунок!
Существуют изменения «слом». Изменение структуры – эволюция модели.
