
- •Формулировка основных (6-8) задач эконометрики (на примере)
- •Регрессия: условная вероятность, условная вероятность распределения, свойства условной вероятности двумерной вероятности распределения.
- •Парная и множественная линейные регрессии
- •Определяемая переменная. Определяющие переменные (факторы). Необходимое условия минимума функции нескольких переменных. Мнк.
- •Трендовые модели. Компоненты: тренд, сезонная, циклическая, календарная, инфляционная и стохастическая компоненты.
- •Классическая декомпозиция:
- •Десезонализация:
- •Теория и свойства оценок параметров регрессии: несмещенность, эффективность, состоятельность
- •Условия гаусса-маркова для стохастической компоненты.
- •Понятия гомо- и гетероскедастичности оценок регрессии.
- •Коэффициент детерминации как мера точности моделирования.
- •Оценка точности прогнозирования (понятие рабочей и контрольной выборок).
- •Практически важные модели парных регрессий: линейная, параболическая, обобщенная экспоненциальная, обратная, логистическая.
- •Структуры моделей регрессии: аддитивная, мультипликативная, аддитивно-мультипликативная (смешанная).
- •Дискретизация динамики социально-экономических показателей (теорема котельникова).
- •Модели динамики с распределенными лагами (виды лагов).
- •Методы идентификации койка моделей с распределенными лагами.
- •Метод ш. Алмон для моделей с распределенными лагами.
- •Метод (модель) адаптивных ожиданий для авторегрессионных моделей.
- •Метода (модель) частичной корректировки для авторегрессионных моделей.
- •Фиктивные переменные в эконометрике.
- •Методы экспоненциального и текущего сглаживания.
- •Модель хольта (линейного роста) и хольта-уинтерса.
- •Модель тейла-вейджа.
Определяемая переменная. Определяющие переменные (факторы). Необходимое условия минимума функции нескольких переменных. Мнк.
Простая регрессия представляет собой регрессию между двумя переменными
—у
и х, т.е.
модель вида
![]() ,
где у
— результативный признак (зависимая);
х
- признак-фактор (объясняющая).
,
где у
— результативный признак (зависимая);
х
- признак-фактор (объясняющая).
Регрессионные модели с одним уравнением. В таких моделях зависимая (объясняемая) переменная у представляется в виде функции: y = f{x,β) = f(x1,...,xk , β1,..., βk), где x1,x2,...,xk - независимые (объясняющие) переменные; β1,..., βk - параметры.
МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака (уpi) от расчетных (теоретических) yi
минимальна:
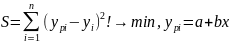
Необходимое и достаточное условие минимума:

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы
минимальной.
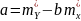
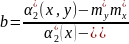
Структурная форма модели содержит эндогенные переменные –У. Это зависимые переменные, число которых равно числу уравнений в системе, и (которые определяются внутри системы). Экзогенные переменные –Х. Это независимые переменные, которые определяются вне системы и влияющие на эндогенные переменные, но независящие от них. Лаговые переменные – независимые переменные за предыдущие моменты времени. Лаговыми могут быть эндогенные переменные за предшествующий период времени, и тогда они являются экзогенными.
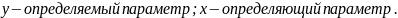
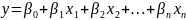
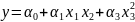 Недостаток
множественной регрессии то, что она
линейна, и следовательно определяющие
переменные независимы друг от друга
(проклятие размерности).
Недостаток
множественной регрессии то, что она
линейна, и следовательно определяющие
переменные независимы друг от друга
(проклятие размерности).
Задачи снижения размерности:
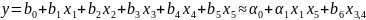
Корреляция
– степень тесноты связи.
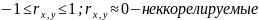
МНК.
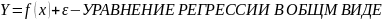
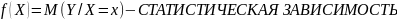

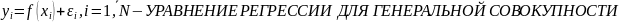
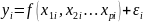
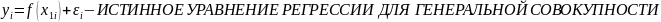
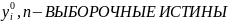
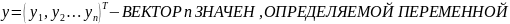
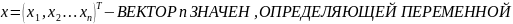
РИСУНОК!
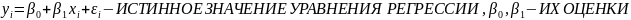

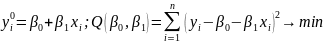
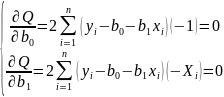
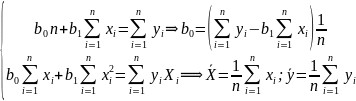
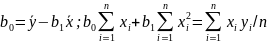
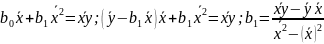
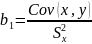
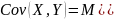
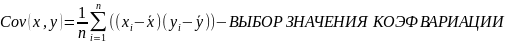
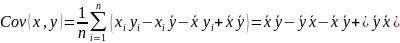

Трендовые модели. Компоненты: тренд, сезонная, циклическая, календарная, инфляционная и стохастическая компоненты.
Тренд представляет собой общую систематическую линейную или нелинейную компоненту, которая может изменяться во времени.
Временной ряд – это последовательность наблюдений некоторой величины в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда (Yt), где t число уровней. Составляющие временного ряда Yt=Ut+Vt+Ct+Et:
Ut – трэнд, плавно меняющаяся компонента, описывает длительное изменение величины;
Vt – сезонная компонента, повторяемость экономических процессов в течении не очень долгого периода времени (месяц, год);
Ct
– циклическая компонента, повторяемость
экономических процессов в течении
длительного периода времени;
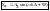
Et – случайная компонента (стохастическая), отражающая влияние не поддающихся учету случайных факторов.
Учет
календарной и инфляционной компонент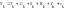 или
или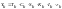
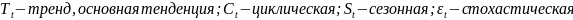
Если
не знаем, есть цикличность или нет
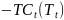
Аддитивная
структура ряда:
(компоненты независимы)
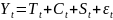 . выражается в тех же единицах, что и
исходный ряд.
. выражается в тех же единицах, что и
исходный ряд.
Рисунок
Мультипликативная
структура:
(взаимосвязь компонентов)
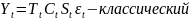
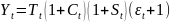 рисунок!!
рисунок!!
Смешанная
структура ряда:
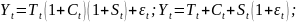
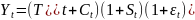
Критерием
декомпозиции может быть и уровень
компонент ряда:
Census I
