Метод Гаусса
Определение 1. Элементарными преобразованиями системы называются:
1) умножение уравнения на число, отличное от нуля;
2) прибавление к одному уравнению другого уравнения, умноженного на некоторое число, отличное от нуля.
3) перестановка двух уравнений;
4) отбрасывание уравнения 0=0.
Если получено уравнение 0=k, то система несовместна.
Метод Гаусса состоит в приведении системы к диагональному виду путем последовательного исключения неизвестных. Количество исключенных неизвестных равно числу линейно независимых уравнений. Переменная считается исключенной, если она содержится только в одном уравнении с коэффициентом 1.
Пример. 
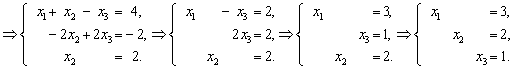Получено
решение системы 
.
Метод Гаусса удобно применять к расширенной матрице системы, левую часть которой с помощью элементарных преобразований матрицы нужно привести кединичной матрице.
Пример. Рассмотрим систему из предыдущего примера. Составим расширенную матрицу:
Получено решение
системы 
.
13)-------------------------------
14)--------------------------------
15)--------------------------------
16Эллипс
Определение 1. Геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, называется эллипсом.
-
каноническое уравнение эллипса.
Исследуем форму эллипса.
1. Найдем точки пересечения с осями.
OX:
y =
0, 
;
OY:
x =
0, 
;
A(a; 0); B (-a; 0); C (0; b); D (0; -b).
Определение 2. Точки A, B, C, D называются вершинами эллипса.
2. Из вида уравнения следует, что линия симметрична относительно осей OX и OY и начала координат.
3.
Следовательно, кривая расположена в прямоугольнике со сторонами 2а и 2b.
Построим данную кривую.
Y
b
-a F1 F2 a
X
-
-b
Определение 3. Отношение фокусного расстояния к большой оси эллипса называется эксцентриситетом эллипса.
.
Определение 4. Параметр a называется большой полуосью эллипса, параметр b называется малой полуосью эллипса.