6. Отрицание (не) – инверсия
Инверсия (от
лат. inversio - переворачивание)
Отрицанием
высказывания
А называют высказывание "не А",
которое истинно, когда А ложно, и ложно,
когда А истинно.
Инверсия обозначается
: не А; ¬А; not A,
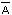
Отрицание
высказывания А можно определить с
помощью таблицы истинности, которая
имеет вид:
Из таблицы
следует, что если А - истинно (А = 1), то
-
ложно (
= О), и наоборот.
Таблица истинности ИЛИ-НЕ, И-НЕ
Входные переменные
|
ИЛИ
y
= x1+x2
|
И
y
= x1x2
|
ИЛИ-НЕ
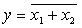
|
И-НЕ
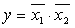
|
x1
|
x2
|
0
0
1
1
|
0
1
0
1
|
0
1
1
1
|
0
0
0
1
|
1
0
0
0
|
1
1
1
0
|
Вычисление значений
логических выражений выполняется в
определенном порядке, согласно их
приоритету:
- инверсия
- конъюнкция
- дизъюнкция
- импликация и
эквивалентность
Операции
одного приоритета выполняются слева
направо. Для изменения
порядка действий
используются скобки.
7. Сложение по модулю 2
Сложе́ние по
модулю 2 —
логическая операция, по своему применению
максимально приближенная к грамматической
конструкции «либо … либо …». Синонимы:
исключа́ющее
«ИЛИ», XOR,
"сумма по модулю 2", сумма Жегалкина.
Эту операцию
нередко сравнивают с дизъюнкцией потому,
что они очень похожи по свойствам, и обе
имеют сходство с союзом «или» в
повседневной речи. Сравните правила
для этих операций:
 истинно, если
истинно
истинно, если
истинно
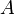 или
или
 ,
или
оба сразу.
,
или
оба сразу.
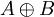 истинно, если
истинно
или
,
но не оба сразу.
истинно, если
истинно
или
,
но не оба сразу.
Таблица истинности:
8. Основные законы и правила алгебры логики
В алгебре логики
законы логики записываются в виде
формул, которые позволяют производить
эквивалентные преобразования логических
выражений.
1. Закон непротиворечия
А * ¬A
= 0
2.Закон исключенного
третьего А + ¬A
= 1
3. Закон двойного
отрицания ¬ ¬А = А
4. Законы Моргана
¬(А
+ В) = ¬
А * ¬
В
¬(А
* В) = ¬
А + ¬
В
5. Закон повторения
А*А = А; А+А = А
6. Правило склеивания
А +АВ = А
7. Правило сложения
с 0 и 1 и умножения с 0 и 1
А+0 = А; А*0 = 0
А +1 = 1; А*1 = 1
Для двоичных
переменных справедливы и общематематические
законы:
1. Коммутативный
закон А*В = В*А; А+В = В+А
2. Ассоциативный
закон А*(В*С) = (А*В)*С; А+(B+С)
= (А+В)+С
3. Дистрибутивный
закон А*(В+С) = А*В+А*С
Пример. Выполнить
преобразование двоичной функции,
используя основные законы алгебры
логики:
F
= A
+ ¬(А
* В) = A
+ ¬A
+ ¬B
= 1 + ¬B
= 1

