
1.В математике для решения разных задач очень часто используют разные функции. А знаете ли вы как их можно задавать и в каких случаях надо использовать тот или иной вид? Для начала рассмотрим определение:
Функция
считается заданной (известной), если
для каждого значения аргумента (из
числа возможных) можно узнать
соответствующее её значение.Наиболее
употребительны три
методы:табличный,графический,аналитический.
Далее остановимся более подробно на
каждом из них.Табличный способ -
общеизвестен (таблицы логарифмов,
квадратных корней и т. д.). Он сразу дает
числовое значение функции. В этом его
преимущество перед другими способами.
Недостатки: таблица трудно обозрима в
целом; она часто не содержит всех нужных
значений аргумента.
![]()
Графический
способ состоит в построении линии
(графика) в разных системах координат,
например в Декартовой – абсциссы (по
горизонтали) изображают значения
аргумента, а ординаты (по вертикали) -
соответствующие значения функции.
Часто бывает, что функция быстро
стремится вверх или вниз, поэтом тогда
удобнее масштабы на осях брать разными.
![]() Преимущества графического способа —
легкость обозрения в целом и непрерывность
изменения аргумента; недостатки:
ограниченная степень точности и
утомительность прочитывания значений
функции с максимально возможной
точностью.Аналитический способ состоит
в задании функции одной или несколькими
формулами, например,y=f(x). Если зависимость
между х и у выражена уравнением,
разрешенным относительно у, то величина
у называется явной функцией аргумента
х, в противном случае — неявной.
Преимущество здесь в том, что всегда
можно вычислить точно значение для
любого аргумента. Недостатки, что по
самой формуле сложно понять общее
поведение функции. Понятие функци-
Преимущества графического способа —
легкость обозрения в целом и непрерывность
изменения аргумента; недостатки:
ограниченная степень точности и
утомительность прочитывания значений
функции с максимально возможной
точностью.Аналитический способ состоит
в задании функции одной или несколькими
формулами, например,y=f(x). Если зависимость
между х и у выражена уравнением,
разрешенным относительно у, то величина
у называется явной функцией аргумента
х, в противном случае — неявной.
Преимущество здесь в том, что всегда
можно вычислить точно значение для
любого аргумента. Недостатки, что по
самой формуле сложно понять общее
поведение функции. Понятие функци-

Сложная
функция. Если функция x=(t)
дифференцируема в точке t0,
а функция y=f(x) дифференцируема в точке
x=x0=(t0),
то сложная функция y=f((t))
дифференцируема в точке t=t0
и ее производная в этой точке находится
по формуле

Док-во:
Т. к. функция y=f(x) дифференцируема в точке x=x0, то y=f ‘(x0)x+(x)x.

2.


3.



![]()

Теорема о связи функции, ее предела и бесконечно малой.
lim (x->a) f(x) = A (A +/- oo) <=> f(x)=A+alpha(x) - бесконечно малая при x->a
сравнение-
Пусть
![]() и
и ![]() – бесконечно малые функции при
– бесконечно малые функции при ![]() .
Предел отношения этих величин может
принимать любые значения – в зависимости
от быстроты убывания одной величины
относительно другой. Для сопоставления
скоростей убывания этих величин при
стремлении x
точке a
можно использовать предел отношения
.
Предел отношения этих величин может
принимать любые значения – в зависимости
от быстроты убывания одной величины
относительно другой. Для сопоставления
скоростей убывания этих величин при
стремлении x
точке a
можно использовать предел отношения![]() Если
этот предел представляет собой конечное
ненулевое число, то
и
называются бесконечно
малыми одного и того же порядка.
Особый интерес представляет частный
случай, когда λ = 1. Тогда говорят,
что
и
являются эквивалентными
бесконечно малыми при
и
записывают это утверждение в виде
Если
этот предел представляет собой конечное
ненулевое число, то
и
называются бесконечно
малыми одного и того же порядка.
Особый интерес представляет частный
случай, когда λ = 1. Тогда говорят,
что
и
являются эквивалентными
бесконечно малыми при
и
записывают это утверждение в виде
![]() Если λ = 0,
то говорят, что
является бесконечно
малой более высокого порядка по
сравнению с
при
Если λ = 0,
то говорят, что
является бесконечно
малой более высокого порядка по
сравнению с
при ![]() а
функция
имеет меньший
порядок малости.
Термин “порядок малости” допускает
уточнение, если
и
а
функция
имеет меньший
порядок малости.
Термин “порядок малости” допускает
уточнение, если
и ![]() представляют собой бесконечно малые
одного и того же порядка. В этом случае
говорят, что
является бесконечно малой n-го
порядка по сравнению с
.
Например, функция
представляют собой бесконечно малые
одного и того же порядка. В этом случае
говорят, что
является бесконечно малой n-го
порядка по сравнению с
.
Например, функция ![]() является бесконечно малой 4-го порядка
по сравнению с
является бесконечно малой 4-го порядка
по сравнению с ![]() при x → 0. Если
λ = ∞, то бесконечно малые
и
как бы меняются своими ролями. В этом
случае функция
является бесконечно малой более высокого
порядка по сравнению с
при
.
при x → 0. Если
λ = ∞, то бесконечно малые
и
как бы меняются своими ролями. В этом
случае функция
является бесконечно малой более высокого
порядка по сравнению с
при
.
4.



![]()
5.

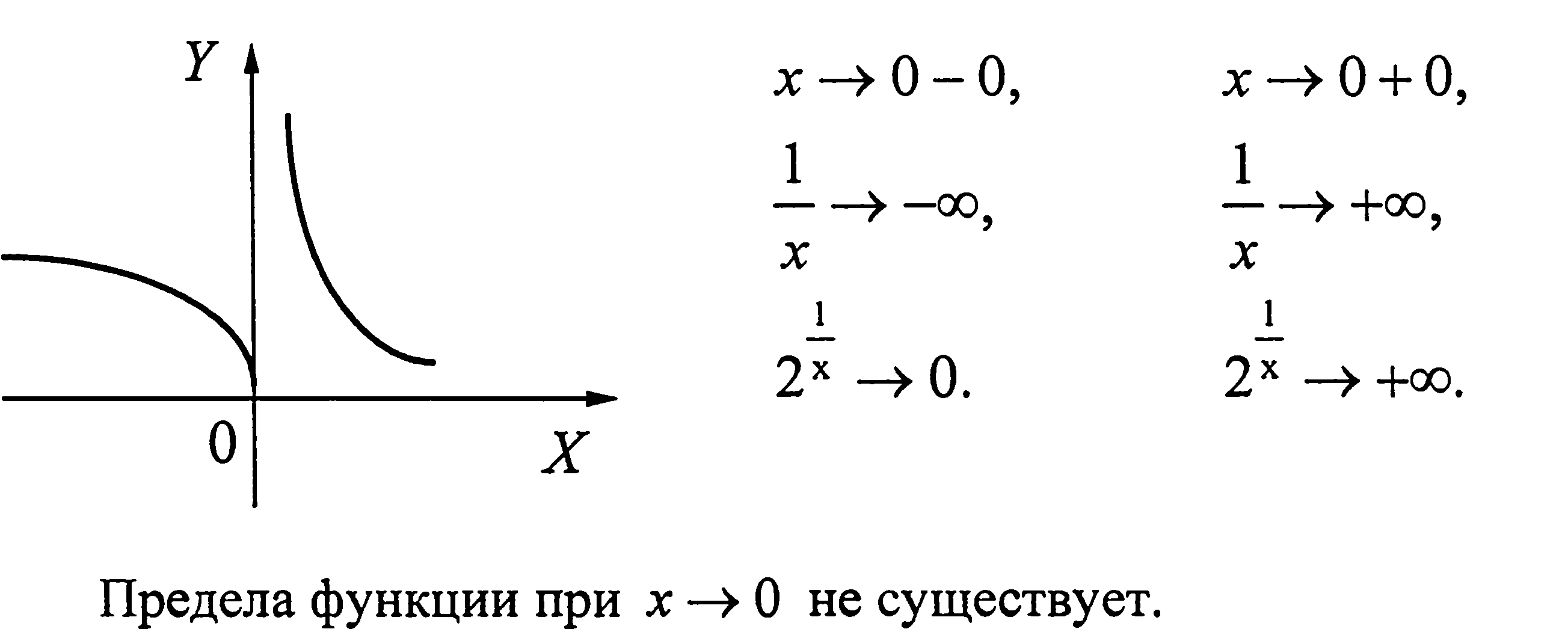
6.

7.

Теорема 1 (необходимое и достаточное условие непрерывности функции в точке).
Для того чтобы, функция у = f(х), определенная в некоторой окрестности точки а, была непрерывна в точке а, необходимо и достаточно, чтобы существовали односторонние пределы и равные друг другу и значению функции в точке а:
f(a-0)=f(a+0)=f(a).
8. Теоремы о непрерывности суммы, произведения, частного непрерывных функций, о непрерывности сложенных функций.
Теорема:
Сумма, произведение и частное двух непрерывных функций – непрерывны. Доказательство: Докажем для произведения.
Пусть ![]() .
Тогда, по теореме о пределе произведения:
.
Тогда, по теореме о пределе произведения:
![]()
Теорема:Пусть
функция ![]() непрерывна
в точке
непрерывна
в точке ![]() ,
а функция
,
а функция ![]() непрерывна
в точке
непрерывна
в точке ![]() .
Тогда сложная функция
.
Тогда сложная функция ![]() ,
состоящая из непрерывных функций,
непрерывна в точке
.Доказательство:
,
состоящая из непрерывных функций,
непрерывна в точке
.Доказательство:
Т.к.
-
непрерывна, то ![]() ,
т.е. при
,
т.е. при ![]() имеем
имеем ![]() .
Поэтом (т.к.
-
непрерывна) имеем:
.
Поэтом (т.к.
-
непрерывна) имеем: ![]()
Непрерывность сложной функции
Пусть
функция у =
φ (x)
непрерывна в точке х0,
а функция f (y)
непрерывна в точке у0 =
φ (x0),
тогда сложная функция f(φ(x))
непрерывна в точке х0.
Доказательство.
Выберем произвольную как угодно малую
окрестность U(z0)
точки z0 = f (y0).
Тогда в силу непрерывности функции f (y)
найдётся такая окрестность V(y0)
точки у0,
что, если у ![]() V(y0),
то значения функции f (y)
U(z0).
Далее, для полученной окрестности V(y0)
в силу непрерывности функции у =
φ (x)
в точке х0 существует
такая окрестность W(x0),
что если х
W(x0),
то значения функции у =
φ(x)
V(y0).
Следовательно, для произвольной
точки х
W(x0)
следует z = f (φ(x))
U(z0).
Что и требовалось доказать.
Это
можно записать ещё и так
V(y0),
то значения функции f (y)
U(z0).
Далее, для полученной окрестности V(y0)
в силу непрерывности функции у =
φ (x)
в точке х0 существует
такая окрестность W(x0),
что если х
W(x0),
то значения функции у =
φ(x)
V(y0).
Следовательно, для произвольной
точки х
W(x0)
следует z = f (φ(x))
U(z0).
Что и требовалось доказать.
Это
можно записать ещё и так
![]() .
.
Указанное выше свойство можно сформулировать в виде правила замены переменной: пусть функция у = φ (x) непрерывна в точке х0, а функция f (y) непрерывна в точке у0 = φ(x0), тогда
![]()
9.

![]()
10.

1) Физический
смысл производной. Если функция
y = f(x) и ее аргумент x являются физическими
величинами, то производная![]() – скорость изменения переменной y
относительно переменной x в точке
– скорость изменения переменной y
относительно переменной x в точке![]() .
Например, если S = S(t) – расстояние,
проходимое точкой за время t, то ее
производная
.
Например, если S = S(t) – расстояние,
проходимое точкой за время t, то ее
производная![]() –
скорость в момент времени
–
скорость в момент времени![]() .
Если q = q(t) – количество электричества,
протекающее через поперечное сечение
проводника в момент времени t,
то
.
Если q = q(t) – количество электричества,
протекающее через поперечное сечение
проводника в момент времени t,
то![]() – скорость изменения количества
электричества в момент времени
,
т.е. сила тока в момент времени
.
2) Геометрический смысл производной.
– скорость изменения количества
электричества в момент времени
,
т.е. сила тока в момент времени
.
2) Геометрический смысл производной.
Пусть ![]() –
некоторая кривая,
–
некоторая кривая,![]() –
точка на кривой
.
–
точка на кривой
.
Любая
прямая, пересекающая
не
менее чем в двух точках
называется секущей.Касательной к
кривой
в
точке
называется
предельное положение секущей ![]() ,
если точка
,
если точка ![]() стремится
к
,
двигаясь по кривой.
стремится
к
,
двигаясь по кривой.
Из
определения очевидно, что если касательная
к кривой в точке
существует,
то она единственнаяРассмотрим кривую
y = f(x) (т.е. график функции y = f(x)).
Пусть в точке ![]() он
имеет невертикальную касательную
он
имеет невертикальную касательную ![]() .
Ее уравнение:
.
Ее уравнение:![]() (уравнение
прямой, проходящей через точку
и
имеющую угловой коэффициент k).
(уравнение
прямой, проходящей через точку
и
имеющую угловой коэффициент k).
По
определению углового коэффициента ![]() ,
где
,
где![]() –
угол наклона прямой
к оси
–
угол наклона прямой
к оси ![]() .
.
Пусть![]() –
угол наклона секущей
к
оси
,
где
–
угол наклона секущей
к
оси
,
где ![]() .
Так как
–
касательная, то при
.
Так как
–
касательная, то при ![]()
![]() ⇒
⇒ ![]() ⇒
⇒ ![]() .
.
Следовательно,
Таким образом, получили, что – угловой коэффициент касательной к графику функции y = f(x) в точке (геометрический смысл производной функции в точке). Поэтому уравнение касательной к кривой y = f(x) в точке можно записать в виде
![]()
12.



13.
![]()

14.

15.
производне
элемент.функций
Таблица
произво=


Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).
Теорема о произв. обратной функции.
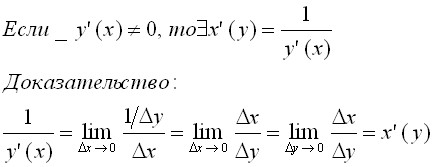
Дифференцирование сложных ф-ций:
Производная сложной ф-ции = произведению производной ф-ции по промежуточному аргументу и производной самого промежуточного аргумента по независимой переменной.
y`=f(x)*U`,или yx`=yU`*Ux`, или dy/dx=dy/dU=dU/dx
Например:
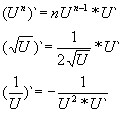
16. Дифференциал функции
Итак,
график дифференцируемой функции в
окрестности каждой своей точки сколь
угодно близко приближается к графику
касательной в силу равенства:![]() где
α – бесконечно малая в окрестности
где
α – бесконечно малая в окрестности ![]() функция.
Для приближенного вычисления значения
функции f в
точке x0 + Δx эту
бесконечно малую функцию можно
отбросить:
функция.
Для приближенного вычисления значения
функции f в
точке x0 + Δx эту
бесконечно малую функцию можно
отбросить:
|
Линейную
функцию ![]() называют дифференциалом
функции f в
точке
и
обозначают df.
Для функции x производная
в каждой точке
равна 1,
то есть
называют дифференциалом
функции f в
точке
и
обозначают df.
Для функции x производная
в каждой точке
равна 1,
то есть ![]() Поэтому
пишут:
Поэтому
пишут: ![]()
|
|
Приближенное
значение функции вблизи точки
равно
сумме ее значения в этой точке и
дифференциала в этой же точке. Это дает
возможность записать производную
следующим образом: ![]()
|
Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.
|
Модель 3.3. Дифференциал функции |
Геометрически дифференциал функции df – это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на dx
Свойства
дифференциаловВыражение
производной через дифференциалы: ![]() где индекс "х" при y' показывает,
что производная берется по аргументу
х. В то же время дифференциалы dy и dx
можно брать по любому аргументу.Выражение
дифференциала через производную:
где индекс "х" при y' показывает,
что производная берется по аргументу
х. В то же время дифференциалы dy и dx
можно брать по любому аргументу.Выражение
дифференциала через производную:
![]() Используя
его, можно записать свойства дифференциалов,
используя свойства
производной.
1. Постоянный множитель можно вынести
за знак дифференциала:
Используя
его, можно записать свойства дифференциалов,
используя свойства
производной.
1. Постоянный множитель можно вынести
за знак дифференциала: ![]()
2.
дифференциал алгебраической суммы
функций равен алгебраической сумме
дифференциалов этих функций
![]() 3. дифференциал произведения
3. дифференциал произведения ![]() 4.
дифференциал дроби (дифференциал
частного)
4.
дифференциал дроби (дифференциал
частного)
![]() 5. дифференциал сложной функции
5. дифференциал сложной функции ![]() где
d g(x), в свою очередь, можно дифференцировать
дальше.
где
d g(x), в свою очередь, можно дифференцировать
дальше.

