Дифференциал.

Пусть функция определена на промежутке Х и дифференцируема в некоторой окрестности точки .

Тогда существует конечная производная .

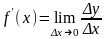По теореме о связи предела и бесконечно малой:

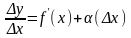, где - бесконечно малая при . Отсюда

.

Таким образом, приращение функции можно представить в виде суммы двух слагаемых: линейного относительно и бесконечно малого при .

Опр. Дифференциалом функции называется главная, линейная относительно часть приращения функции, равная произведению производной на приращение аргумента:

.

Рассмотрим функцию у=х и найдем ее дифференциал.

. Таким образом, формула дифференциала может быть записана в виде:

.

Пример. Найти дифференциал функции .

.

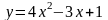Выясним геометрический смысл дифференциала. Из : . Таким образом, дифференциал есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда х получает приращение .

С войства дифференциала аналогичны свойствам производной:

1. d(С)=0;

2. d(u+v)=du+dv;

3. d(uv)=vdu+udv;

4. ;

5. Форма дифференциала инвариантна (неизменна): он всегда равен произведению производной на дифференциал аргумента, независимо от того, простым или сложным является аргумент.

Опр. Дифференциалом второго порядка (или вторым дифференциалом) 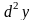называется дифференциал от дифференциала функции, т.е.:

.

Аналогично, дифференциалом п-го порядка называется дифференциал от дифференциала (п-1)-го порядка этой функции: .

20.Эластичность функции, ее свойства. Эластичность спроса по цене.

21.Возрастание и убывание функций. Критерий монотонности функции.

Возрастание и убывание функций.

Теорема (критерий монотонности дифференцируемой функции). Пусть функция непрерывна на промежутке и дифференцируема во всех его внутренних точках. Тогда:

- для монотонного возрастания функции необходимо и достаточно, чтобы в 0;

- для монотонного убывания функции необходимо и достаточно, чтобы в (а,в) 0;

- для постоянности функции необходимо и достаточно, чтобы в (а,в) =0.

Док-во. Докажем достаточность для возрастающей функции. Выберем произвольно точки . По теореме Лагранжа найдется точка , такая что 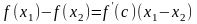. Т.к. оба множителя в правой части неотрицательны, то , т.е. . Следовательно, функция является монотонно возрастающей.

Докажем необходимость для возрастающей функции. Пусть f(x) – монотонно возрастает. Тогда , следовательно в (а,в).

Для убывающей функции доказательства аналогичны.

Докажем необходимость для постоянной функции. Если f(x)=const в (а,в), то .

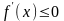Докажем достаточность для постоянной функции. Пусть в (a,b). Тогда тем более в (a,b). Тогда по доказанному выше функция монотонно возрастает в (a,b), т.е. . С другой стороны, если в (a,b), то тем более в (a,b). Тогда по доказанному выше функция монотонно убывает в (a,b), т.е. . Одновременное выполнение этих условий возможно лишь при .▲

Пример. Найти промежутки монотонности функции .

Найдем производную . Очевидно, что при производная , функция является возрастающей. При производная , функция убывает.

22.Экстремумы функции. Необходимое и достаточное условия локального экстремума.