
- •Понятие функции
- •Свойства.
- •Числовые последовательности.
- •Предел числовой последовательности.
- •Предел функции. Предел функции в точке. Односторонние пределы.
- •Бесконечные пределы.
- •Свойства
- •Необходимые условия существования конечного предела функции.
- •Достаточные условия существования конечного предела функции.
- •Непрерывность функции в точке.
- •Точки разрыва, их классификация.
- •Непрерывность функции на множестве.
- •Дифференцируемость функции.
- •Основные правила дифференцирования.
- •Уравнение касательной к графику функции.
- •Производные высших порядков.
- •Правило Лопиталя
- •Дифференциал.
- •Возрастание и убывание функций.
- •Экстремумы функции.
- •Выпуклость функции. Точки перегиба.
- •Асимптоты графика функции.
- •Свойства неопределенного интеграла.
- •Непосредственное интегрирование.
- •Метод замены переменной в неопределенном интеграле.
- •Интегрирование рациональных функций.
- •Метод интегрирования по частям в неопределенном интеграле.
- •Метод интегрирования подстановкой.
- •§1. Определенный интеграл.
- •Свойства определенного интеграла.
- •Вычисление определенного интеграла.
- •Интегрирование по частям в определенном интеграле.
- •Приложения определенного интеграла.
- •Вычисление объемов тел вращения
Основные правила дифференцирования.
1. Производная алгебраической суммы конечного числа дифференцируемых функций равна сумме производных этих функций:
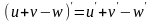 .
.
2. Производная произведения двух дифференцируемых функций равна сумме произведения производной первого множителя на второй множитель и произведения первого множителя на производную второго:
 .
.
Следствие 1. Постоянный множитель
можно вынести за знак производной:
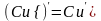 .
.
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные:
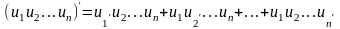 .
.
3. Производная частного двух
дифференцируемых функций может быть
найдена по формуле:
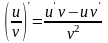 (
( ).
).
Докажем, например, правило 2 (правила1-3 докажите самостоятельно).
Рассмотрим функцию
 .
Дадим аргументу
.
Дадим аргументу
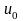 приращение
приращение
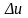 ,
аргументу
,
аргументу
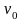 приращение
приращение
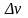 .
Соответственно, их произведение получит
приращение
.
Соответственно, их произведение получит
приращение
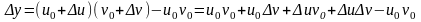 .
.
Составим отношение
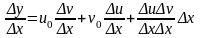 .
Переходя в этом равенстве к пределу при
,
получим:
.
Переходя в этом равенстве к пределу при
,
получим:
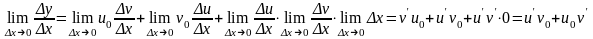
4. Дифференцирование обратной функции.
Если функция
имеет
обратную функцию
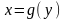 и
и
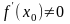 ,
то обратная функция дифференцируема в
точке
,
причем
,
то обратная функция дифференцируема в
точке
,
причем
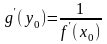 .
.
5.
Конец формы
Дифференцирование сложной функции.
Если функции
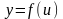 и
и
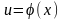 дифференцируемы по своим аргументам,
то производная сложной функции
дифференцируемы по своим аргументам,
то производная сложной функции
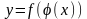 существует и равна произведению
производной внешней функции по
промежуточному аргументу и производной
промежуточного аргумента по независимой
переменной:
существует и равна произведению
производной внешней функции по
промежуточному аргументу и производной
промежуточного аргумента по независимой
переменной:
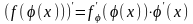 .
.
Таким образом, производные сложных функций можно вычислить по формулам:
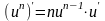
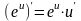

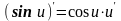

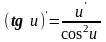
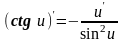
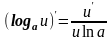
17.Уравнение касательной к графику функции.
Уравнение касательной к графику функции.
Выведем уравнение касательной к графику
функции
в точке
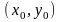 .
.
Будем искать это уравнение в виде у=кх+в.
Т.к. прямая проходит через данную точку, то
 ,
откуда
,
откуда
 .
.
Тогда
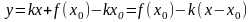 .
А поскольку
.
А поскольку
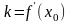 ,
то
,
то
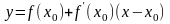 - уравнение касательной.
- уравнение касательной.
Пример. Составить уравнение
касательной к графику функции
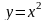 в точке (2;4).
в точке (2;4).
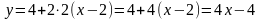 .
.
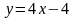 .
.
18.Производные высших порядков. Правило Лопиталя.
Производные высших порядков.
Если функция дифференцируема в точке, то она имеет производную в этой точке, которая также является функцией от х и также может быть дифференцируемой.
Производной второго порядка или
второй производной
 функции
называется производная от ее производной:
функции
называется производная от ее производной:
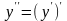 .
.
Вторая
производная также может быть обозначена
символами
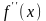 ,
,
 .
.
Аналогично определяется и обозначается производная третьего порядка:
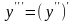 .
.
Для обозначения производных более
высокого порядка используются арабские
цифры в скобках или римские цифры,
например:
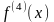 или
или
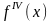 .
.
Опр. Производной n-го
порядка называется производная
от производной (n-1)-го
порядка:
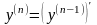 .
.
Пример.
Найти вторую производную функции
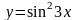 .
.
Решение.
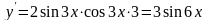 ;
;
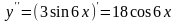 .
.
Правило Лопиталя
предлагает эффективный способ раскрытия
неопределенностей
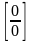 и
и
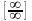 .
.
Теорема. Предел отношения двух дифференцируемых бесконечно малых или бесконечно больших функций равен пределу отношения их производных (если он существует, конечен или бесконечен):
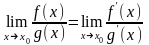 .
.
Пример1.
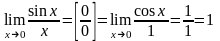 .
.
Пример 2.
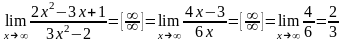 .
.
Пример 3.
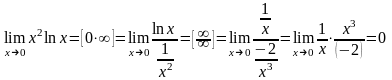 .
.
Пример 4.
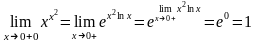 .
.
19.Дифференциал. Геометрический смысл дифференциала. Связь между производной и дифференциалом. Свойства дифференциала.
