Дифференцируемость функции.

Опр. Числовая функция y=f(x) называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде:

,

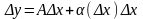где А – некоторое число, 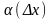- функция от , являющаяся бесконечно малой при .

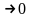Утв. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Теорема1 (о связи между непрерывностью и дифференцируемостью).

Если функция дифференцируема в точке, то она непрерывна в этой точке.

Док-во. Пусть функция y=f(x) дифференцируема в точке . Тогда, по определению, ее приращение можно представить в виде . Переходя в этом равенстве к пределу при , получим:

, что соответствует определению непрерывности функции.▲

Теорема 1 является необходимым (но не достаточным) признаком дифференцируемости функции в точке. Обратная теорема, вообще говоря, не верна, т.е. если функция непрерывна в точке, то она не обязательно дифференцируема в этой точке.

15.Теоремы Ферма, Ролля, Лагранжа (все с доказательством).

Теорема Ферма. Пусть функция определена и дифференцируема на интервале (а,в) и в некоторой точке принимает наибольшее или наименьшее значение. Тогда =0.

Док-во. Пусть - наибольшее значение функции на интервале (а,в). Тогда при : , .

При : , .

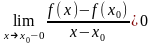Если функция по условию дифференцируема в т. , то указанные выше пределы должны совпадать. А это возможно лишь при =0.▲

Геометрически теорема Ферма означает, что в точках наибольшего или наименьшего значений дифференцируемой функции касательная к графику функции имеет нулевой угловой коэффициент, т.е. параллельна оси Ох.

Теорема Ролля (о среднем). Пусть функция :

1) непрерывна на отрезке ;

2) дифференцируема на интервале ;

3) принимает на концах интервала равные значения: f(a)=f(b).

Тогда существует т. 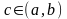, такая, что .

Док-во. По второй теореме Вейерштрасса непрерывная на отрезке функция достигает на нем своего наибольшего и наименьшего значений. Если оба эти значения достигаются на концах отрезка, а по условию они равны, следовательно, функция постоянна и ее производная равна нулю. Если хотя бы одно из этих значений достигается внутри отрезка, то по теореме Ферма. ▲

Замечание. Если f(a)=f(b)=0, то теорему Ролля можно сформулировать так: между двумя последовательными нулями дифференцируемой функции имеется хотя бы один нуль производной.

Теорема Лагранжа (о среднем). Пусть функция :

1) непрерывна на отрезке ;

2) дифференцируема на интервале .

Тогда существует т. , такая, что .

(или , эта формула называется формулой конечных приращений).

Док-во. Введем новую функцию . Она непрерывна на отрезке , дифференцируема на интервале и g(a)=g(b). Т.о., эта функция удовлетворяет условиям теоремы Ролля. Следовательно, существует т. , такая, что или:

, откуда . ▲

16.Правила дифференцирования (одно с доказательством)