Непрерывность функции в точке.

Пусть функция и точка .

Опр. Функция называется непрерывной в точке , если

.

Пример. Докажем, что функция является непрерывной в каждой точке . Возьмем произвольное . Положим . Тогда если , то .

Сравнивая определение непрерывности с определением предела функции в точке, можно сделать вывод, что функция непрерывна в точке, если .

Поскольку условием существования конечного предела функции в точке является существование и равенство односторонних пределов функции в этой точке, непрерывность функции в точке можно понимать как выполнение трех условий:

1) функция определена в точке .

2) существуют и равны оба односторонних предела функции в точке .

3) значение функции равно значению предела в точке .

Примером функции, не являющейся непрерывной ни в одной точке является функция Дирихле.

В случае, если является граничной точкой области определения функции говорят об односторонней непрерывности функции.

Свойства непрерывных функций.

1. Пусть числовые функции и непрерывны в точке . Тогда их сумма и произведение также непрерывны в этой точке. Если, кроме того, , то и частное этих функций тоже будет непрерывно в точке .

2. Пусть непрерывна в т. , непрерывна в т. . Тогда суперпозиция этих функций непрерывна в точке .

3. Если функция непрерывна , то можно менять местами символы функции и предела, например: .

10.Классификация точек разрыва функции. Непрерывность функции на множестве.

Точки разрыва, их классификация.

Опр. Точки, в которых функция не является непрерывной , называют точками разрыва функции.

Точка называется точкой разрыва первого рода, если в этой точке существуют конечные односторонние пределы.

Точка разрыва первого рода называется точкой устранимого разрыва, если односторонние пределы в этой точке равны (в противном случае она называется точкой неустранимого разрыва).

Скачком функции в точке неустранимого разрыва называется разность значений односторонних пределов в этой точке.

Точка называется точкой разрыва второго рода, если в этой точке хотя бы один из односторонних пределов бесконечен или не существует.

Пример.

,

x=0 – точка разрыва, т.к. функция не определена в этой точке;

Т.к. односторонние пределы в 0 бесконечны, то это точка разрыва II рода.

x=0 – точка устранимого разрыва (I рода), т. к. значение предела конечно, хотя и не равно значению функции в этой точке.

х=0 – точка разрыва, т.к. односторонние пределы не равны.

Поскольку односторонние пределы конечны, то это разрыв I рода со скачком, равным 2.

Непрерывность функции на множестве.

Опр. Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.

Все основные элементарные функции непрерывны в области определения.

Пример.

Исследовать на непрерывность функции:

; ;

11.Свойства функций, непрерывных на отрезке.

Свойства функций, непрерывных на отрезке.

Теорема 1 (Вейерштрасса). Если функция , заданная на , непрерывна на этом отрезке, то она ограничена на этом отрезке, т.е. .

Теорема 2 (Вейерштрасса). Непрерывная на функция принимает на этом отрезке наибольшее и наименьшее значения.

Теорема 3 (о промежуточном значении). Пусть функция , заданная на , непрерывна на этом отрезке и принимает на концах этого отрезка неравные значения. Тогда она принимает и все значения, расположенные на числовой оси между f(a) и f(b).

В частности, если непрерывная на функция принимает на концах этого отрезка значения разных знаков, то существует точка , такая, что f(c)=0.

12.Производная. Геометрический смысл производной.

Понятие производной функции.

Пусть функция определена и непрерывна на промежутке X.

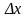
Возьмем точку . Дадим аргументу x приращение 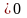так, чтобы 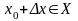. Тогда функция получит приращение .

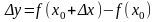Опр. Производной функции в данной точке называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю (если этот предел существует):

Производную функции обозначают также , . Нахождение производной функции называется дифференцированием этой функции.

Выясним геометрический смысл производной. Проведем секущую АВ. Из следуют соотношения: .

При точка В будет двигаться по дуге к т. А, и секущая АВ будет стремиться к положению касательной, т.е.

,

где - угол между касательной к графику в т. и положительным направлением оси Ох. Таким образом, в геометрическом смысле производная функции в точке представляет собой угловой коэффициент (тангенс угла наклона) касательной, проведенной к графику функции в этой точке.

13.Производные основных элементарных функций (одна с выводом).

Функция	Производная		Функция	Производная
C	0

14.Дифференцируемость функции. Связь между непрерывностью и дифференцируемостью.