Необходимые условия существования конечного предела функции.

Теорема (о локальной ограниченности) . Для существования конечного предела функции в точке необходимо, чтобы в некоторой окрестности этой точки (за исключением самой точки) функция была ограничена.

Теорема (о локальном повторении функцией свойств предела). Для существования в точке конечного предела необходимо, чтобы в некоторой окрестности этой точки (за исключением самой точки) .

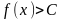7. Условия существования конечного предела функции (одно с доказательством).

Достаточные условия существования конечного предела функции.

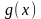Теорема (об арифметике). Если для и существуют конечные пределы, то для их суммы и произведения также существуют конечные пределы, причем:

;

.

Если 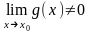, то существует конечный предел частного:

.

Док-во. Докажем, например, второе равенство.

Пусть существуют конечные пределы и . Докажем, что существует конечный предел .

Итак, мы должны доказать, что:

.

Возьмем произвольное . Найдем из условия , т.е. для этого : .

Найдем из условия , т.е. для этого :

.

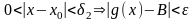Т.к. для по условию существует конечный предел в т. , то эта функция будет ограниченной в некоторой окрестности т. (по теореме о локальной ограниченности), т.е. 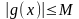- некоторой константы.

Положим . Проверим, что это - искомое. Действительно,

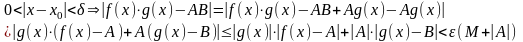
В силу произвольности можно считать утверждение доказанным (или можно было искать не по , а по ). ▲

Теорема (о промежуточной функции). Пусть для функций и существуют конечные пределы в т. , равные друг другу, и в некоторой окрестности т. , за исключением самой этой точки, выполняется условие:

. Тогда для тоже существует конечный предел в т. , равный значению пределов функций и .

Теорема (о пределе монотонной ограниченной функции). Если функция монотонно возрастает (убывает) в некоторой окрестности т. и ограничена сверху (снизу), то она имеет в этой точке соответствующий односторонний предел.

8.Замечательные пределы (1-й с док.).

Замечательные пределы.

Теорема 1 (первый замечательный предел). Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:

.

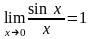Док-во. Рассмотрим круг радиуса R с центром в точке О. Пусть сначала . Из рисунка видно, что .

;

;

.Таким образом,

.

Разделив обе части этого выражения на

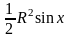>0, получим:

или .

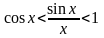Переходя в этом неравенстве к пределу при , получим: .

По теореме о промежуточной функции .

При полученные выводы также будут справедливы (доказать самостоятельно).▲

Следствия. ; ; .

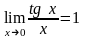Теорема 2 (второй замечательный предел). Числовая последовательность имеет конечный предел, равный числу е:

, ( )

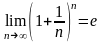Следствия. ; .

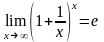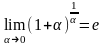Примеры.

; .

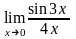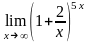9.Непрерывность функции в точке. Свойства функций, непрерывных в точке.