Вычисление объемов тел вращения

Пусть функция y=f(x)непрерывна и неотрицательна на отрезке [а,в]. Тогда тело, образуемое при вращении вокруг оси Ох криволинейной трапеции, ограниченной графиком этой функции, осью Ох и прямыми х=а и х=в вычисляется по формуле

.

Если тело образовано вращением вокруг оси криволинейной трапеции, ограниченной непрерывной кривой , отрезками прямых и осью , то объем вращения вычисляется по формуле

.

33. Несобственные интегралы первого рода.

Понятие определенного интеграла было дано в предположении, что отрезок интегрирования конечен, а подынтегральная функция ограничена на этом отрезке. Если хотя бы одно из этих условий нарушено, то соответствующие интегралы называются несобственными. Рассмотрим два вида несобственных интегралов.

Несобственные интегралы с бесконечными пределами интегрирования.

Пусть промежутком интегрирования является луч , а функция y=f(x) интегрируема на каждом конечном отрезке [a,b]. Геометрически задача состоит в нахождении площади под кривой. Возьмем точку в, найдем площадь кр.тр.через опр. инт. и устремим в к .

Н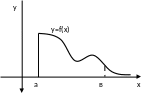 есобственным интегралом

называют предел функции верхнего предела интегрирования при его стремлении к бесконечности:

= .

Если указанный предел существует и конечен, то говорят, что несобственный интеграл существует или сходится, если конечный предел не существует – то говорят, что несобственный интеграл не существует или расходится.

П усть теперь промежутком интегрирования является луч .

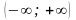Тогда аналогично вводится понятие несобственного интеграла с бесконечным нижним пределом:

= .

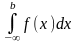Аналогично определяется несобственный интеграл с двумя бесконечными пределами. В этом случае числовую ось разбивают произвольной точкой с на два луча и полагают

+ .

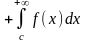Если оба несобственных интеграла в правой части сходятся, то сходится и несобственный интеграл в левой части, причем его значение не зависит от выбора промежуточной точки с (доказать самостоятельно).

В геометрическом смысле несобственный интеграл от неотрицательной функции равен площади неограниченной криволинейной трапеции.

34.Несобственные интегралы второго рода.

Несобственные интегралы от неограниченных функций.

Пусть функция y=f(x) определена на промежутке . В точке в функция не ограничена, но ограничена в отрезке (точку в назовем тогда особой точкой). Тогда несобственным интегралом от неограниченной функции y=f(x) называют предел функции верхнего предела интегрирования при слева:

= .

Если указанный предел существует и конечен, то говорят, что несобственный интеграл сходится (в противном случае – расходится).

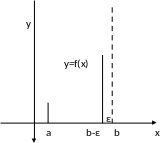
Аналогично, если а – особая точка: если функция не ограничена в точке а, но ограничена на любом меньшем отрезке , то несобственный интеграл определяют так:

.

Если единственной особой точкой на отрезке [a,b] является точка 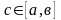, то полагают

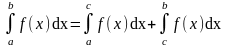
при условии, что оба несобственных интеграла в правой части сходятся.

Если особых точек на отрезке [a,b] несколько, то отрезок разбивают таким образом, чтобы в каждой части было не более одной особой точки и используют последнее определение.

Для вычисления несобственных интегралов от неограниченных функций также может быть использован аналог формулы Ньютона − Лейбница. Например, для несобственного интеграла с особыми точками а и в :

,

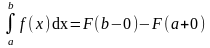где , .

Пример 1. Найти интеграл .

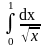Данный интеграл – несобственный, т.к. подынтегральная функция на отрезке интегрирования имеет особую точку х=0. Тогда

.

Или по упрощенной формуле (Ньютона – Лейбница):

.

Пример 2. Найти интеграл .

Подынтегральная функция имеет на промежутке интегрирования единственную особую точку х=1.

= .

Следовательно, данный несобственный интеграл расходится.

Пример 3. Найти интеграл .

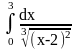Имеем несобственный интеграл с особой точкой х=2. Тогда

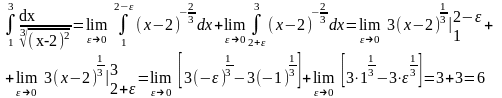
Следовательно, данный несобственный интеграл сходится к значению 6.