Свойства определенного интеграла.
1.
;
2.
;
3.
;
4.
;
5. Пусть функция y=f(x) интегрируема на отрезках [a,c] [b,c], a<c<b. Тогда она интегрируема и на отрезке [a,b] , причем
;
6. Если функции f(x) и g(x) интегрируемы по отрезку [a,b], то и их сумма также интегрируема по отрезку [a,b], причем
.
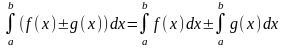7. Если на отрезке [a,b]
выполняется неравенство
,
то
.
8. Если промежуток интегрирования симметричен, то
,
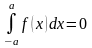если
- нечетная функция,
и
,
если
- четная функция.
Вычисление определенного интеграла.
Пусть функция y=f(x)
определена и непрерывна на отрезке
[a,b].
Тогда она интегрируема как на отрезке
[a,b],
так и на любом меньшем отрезке [а,х],
где
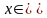[a,b].
Значит, величина
является функцией от х. Она называется интегралом с переменным верхним пределом и является первообразной для функции f(x). Другими словами, функция Ф(х) в каждой своей точке имеет производную, равную f(x):
.
Теперь перейдем к вопросу вычисления определенного интеграла.
Теорема. Пусть функция y=f(x) определена и непрерывна на отрезке [a,b] и F(х) является первообразной для функции f(x). Тогда
.
(Эта основная формула интегрального исчисления называется формулой Ньютона-Лейбница. Она позволяет сводить вычисление определенного интеграла к нахождению первообразной.)
Док-во. Пусть функция y=f(x) имеет некоторую первообразную F(x). Тогда F(x)=Ф(x)+C, где - другая первообразная f(x). Имеем:
.▲
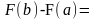
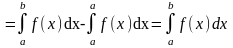Пример.
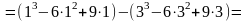1-6+9-27+54-27=4.
Замена переменной в определенном интеграле.
Теорема. Пусть функция y=f(x) непрерывна на отрезке [a,b], а функция x=φ(t) определена на отрезке [α,β] и имеет непрерывную производную внутри этого отрезка, причем φ(α)=a, φ(β)=b и φ([α,β])=[a,b]. Тогда
.
Док-во. Пусть F(x)
– первообразная для функции f(x),
тогда
и
.
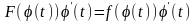Тогда
.▲
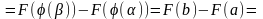
Интегрирование по частям в определенном интеграле.
Если функции
и
непрерывны вместе со своими производными
на отрезке
,
то имеет место следующая формула
интегрирования по частям:
.
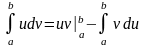32.Приложения определенного интеграла.
Приложения определенного интеграла.
1. Для непрерывной неотрицательной на отрезке [а,в] функции y=f(x) площадь фигуры, ограниченной графиком этой функции, осью Ох и прямыми х=а и х=в вычисляется по формуле:
.
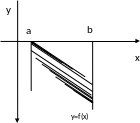
2. Для непрерывной неположительной на отрезке [а,в] функции y=f(x) площадь фигуры, ограниченной графиком этой функции, осью Ох и прямыми х=а и х=в вычисляется по формуле:
.
3.
Пусть
на отрезке [а,в].
Тогда площадь фигуры, ограниченной
сверху графиком f(x),
снизу графиком g(x)
и прямыми х=а
и х=в
вычисляется по формуле:
.
Отметим, что данная формула выполняется и в случае, когда функции f и g отрицательны.
4.
Площадь криволинейной трапеции,
прилегающей к оси
,
вычисляется по формуле
.
Пример. Найти
площадь фигуры, ограниченной линиями
и у=х.
Р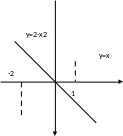
ешение.
Найдем точки пересечения двух данных
линий.
2-х2=х
х2+х-2=0
х=1 и х=-2.
Таким образом,
=
=
(кв.ед.)