Свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции, дифференциал от неопределенного интеграла равен подынтегральному выражению.

Док-во. Пусть функция f(x) имеет первообразную F(x), тогда

ò f(x)dx = F(x) + c. Найдем производную и дифференциал от обеих частей равенства.

(ò f(x)dx)' = (F(x) + c)' = f(x),

d(ò f(x)dx) = (ò f(x)dx)' dx = f(x)dx.

2. Интеграл от дифференциала функции равен этой функции с точностью до постоянного слагаемого: ò d F(x) = F(x) + C.

Док-во. ò d F(x) = ò F'(x)dx= ò f(x)d x = F(x) + C.

Из свойств 1 и 2 следует, что операции дифференцирования и интегрирования являются взаимно обратными.

3. Постоянный множитель можно вынести за знак интеграла:

ò k f(x)dx = k ò f(x)dx.

Док-во. Пусть функция f(x) имеет первообразную F(x).

ò f(x)dx = F(x) + C. Умножим обе части на k .

k ò f(x)dx = k F(x) + C₁, где C₁ = k C_.

Найдем производную функции kF(x).

(k F(x))' = k f(x).

Функция k F(x) является первообразной функции k f(x). Следовательно,

ò k f(x)dx = k F(x) + C,

ò k f(x)dx = k ò f(x)dx.

4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций.

29.Методы интегрирования в неопределенном интеграле.

Непосредственное интегрирование.

Этот вид интегрирования состоит в приведении исходного интеграла к одному или к нескольким табличным с помощью свойств интеграла и тождественных преобразований.

.

Метод замены переменной в неопределенном интеграле.

Если независимую переменную х интегрирования заменить некоторой функцией и(х), дифференцируемой по х, то формула интегрирования не изменится. Во многих случаях введение новой переменной позволяет упростить подынтегральное выражение и свести интеграл к одному или нескольким табличным.

Пример 1.

При линейной замене переменных u=ax+b интеграл сводится к табличному введением уравнивающего множителя .

Новую переменную можно не выписывать явно. В таких случаях говорят о введении постоянных и переменных под знак дифференциала или о тождественном преобразовании дифференциала.

Интегрирование рациональных функций.

Рассмотрим интеграл вида , где P(x) и Q(x) – многочлены (такие функции называют рациональными функциями).

Если эта дробь неправильная, то можно выполнить деление с остатком и представить подынтегральную функцию в виде суммы многочлена и правильной дроби.

Например, рассмотрим неправильную дробь

• Интеграл вида находят путем выделения полного квадрата в знаменателе и сведения к табличному интегралу (8) или (10).

(Интеграл вида 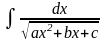находят путем выделения полного квадрата в знаменателе и сведения к табличному интегралу (9) или (11)).

• Интегралы вида 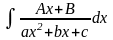(и ) находят путем выделения в числителе производной знаменателя и сведения к интегралам рассмотренных выше видов.

Если подынтегральная функция не соответствует ни одному из перечисленных выше видов, то для взятия интеграла используют тот факт, что любую правильную дробь можно представить в виде суммы простых дробей с помощью следующих теорем.

Теорема 1. Каждый многочлен Q(x) с действительными коэффициентами может быть представлен единственным образом в виде

, (1) где a, b, …,- корни многочлена кратности k, l, … ;

квадратичные множители кратности m, n,… не имеют действительных корней.

Теорема 2. Пусть - правильная рациональная дробь, у которой знаменатель представлен в виде (1). Тогда эту дробь можно единственным образом представить в виде суммы простых дробей:

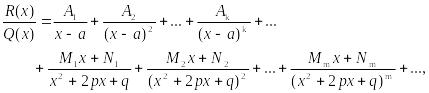, (2)

где - некоторые действительные числа.

Выражение (2) называется разложением рациональной дроби на простые дроби, числа - коэффициентами разложения.

Для определения коэффициентов разложения используют метод неопределенных коэффициентов, который состоит в следующем: приводят левую часть равенства (2) или (3) к общему знаменателю и приравнивают коэффициенты при одинаковых степенях многочлена, полученного в числителе и многочлена R(x).