1.Понятие функции. Основные элементарные функции, их свойства.
Понятие функции
Пусть Х и У – некоторые множества.
Опр. Если каждому элементу
ставится
в соответствие по некоторому правилу
единственный элемент
,
то говорят, что на множестве Х задана
функция (функциональная зависимость)
со значениями в множестве У:
,
.
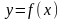Множество Х называется областью определения функции и обозначается D(f), множество У называется областью значений функции и обозначается I(f).
Свойства.
Опр. Числовая функция y=f(x) называется монотонно возрастающей (убывающей), если большему значению аргумента соответствует большее (меньшее) значение функции:
.
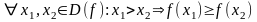Опр. Числовая функция y=f(x) называется ограниченной сверху на множестве А, если найдется число М такое, что:
.
Опр. Числовая функция y=f(x) называется ограниченной снизу на множестве А, если найдется число М такое, что:
.
Опр. Числовая функция y=f(x) называется ограниченной на множестве А, если найдется число К такое, что:
.
В противном случае функция называется неограниченной.
Числовая функция y=f(x)
называется четной, если
;
числовая функция называется нечетной,
если
.
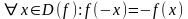Числовая функция y=f(x)
называется периодической, если
найдется такое число Т>0, что
.
2.Числовая последовательность. Предел числовой
последовательности.
Числовые последовательности.
Опр. Функция, заданная на множестве натуральных чисел, называется числовой последовательностью.
Т. е., если каждому натуральному числу
n поставлено в
соответствие определенное число
,
то говорят, что задана числовая
последовательность
:
1 2 3 … n … - аргумент
…
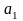
… - члены последовательности.
- общий член последовательности. Чтобы задать числовую последовательность, необходимо указать формулу ее общего члена. Примеры числовых последовательностей:
:
2, 4, 8, …..,
,…,
:
,
,
,
…,
,
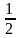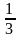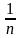… и т.д.
Предел числовой последовательности.
Рассмотрим числовую последовательность
.
Изобразим ее на числовой оси.
Очевидно, что члены последовательности убывают по величине, но при этом положительны и не равны нулю. При достаточно больших номерах члены последовательности будут сколь угодно близкими к 0. В этом случае говорят, что 0 является пределом данной числовой последовательности.
Опр. Число А называется пределом
числовой последовательности
,
если для любого, даже сколь угодно малого
положительного числа
,
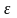найдется такой номер N,
зависящий от
,
что для всех членов последовательности
с номерами n>N,
верно неравенство:
.
Если последовательность
имеет предел, равный А, то она
называется сходящейся к числу А (в
противном случае – расходящейся). Кратко
это можно записать так:
.
(Или так:
).
Используя логические символы, определение предела числовой последовательности можно записать так:
.
Смысл определения состоит в том, что при достаточно больших номерах все члены последовательности (начиная с некоторого), будут заключены в - окрестности предельной точки, какой бы узкой она ни была.
Замечание.
Числовая последовательность может
иметь предел, равный
,
а может не иметь предела
3.Предел функции (два определения). Односторонние пределы. Бесконечные пределы.