Математика / Теория / 14 Функции многих переменных

Функции многих переменных

§1. Понятие функции многих переменных.

Пусть имеется n переменных величин . Каждый набор обозначает точку n-мерного множества (п-мерный вектор).

Пусть даны множества и .

Опр. Если каждой точке ставится в соответствие единственное число , то говорят, что задана числовая функция n переменных:

.

называют областью определения, - множеством значений данной функции.

В случае n=2 вместо обычно пишут x, y, z. Тогда функция двух переменных имеет вид:

z=f(x,y).

Например, - функция двух переменных;

- функция трех переменных;

- линейная функция n переменных.

Опр. Графиком функции n переменных называется n-мерная гиперповерхность в пространстве , каждая точка которой задается координатами

.

Например, графиком функции двух переменных z=f(x,y) является поверхность в трехмерном пространстве, каждая точка которой задается координатами (x,y,z), где , и .

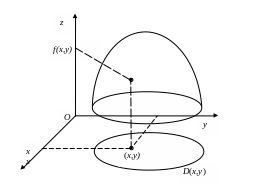
Поскольку график функции трех и более переменных изобразить не представляется возможным, в основном мы будем (для наглядности) рассматривать функции двух переменных.

Построение графиков функций двух переменных является довольно сложной задачей. Существенную помощь в ее решении может оказать построение так называемых линий уровня.

Опр. Линией уровня функции двух переменных z=f(x,y) называется множество точек плоскости ХОУ, являющихся проекцией сечения графика функции плоскостью, параллельной ХОУ. В каждой точке линии уровня функция имеет одно и то же значение. Линии уровня описываются уравнением f(x,y)=с, где с – некоторое число. Линий уровня бесконечно много, и через каждую точку области определения можно провести одну из них.

Опр. Поверхностью уровня функции n переменных y=f ( ) называется гиперповерхность в пространстве , в каждой точке которой значение функции постоянно и равно некоторому значению с. Уравнение поверхности уровня: f ( )=с.

Пример. Построить график функции двух переменных

.

.

При с=1: ; .

При с=4: ; .

При с=9: ; .

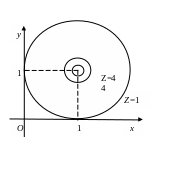
Линии уровня – концентрические окружности, радиус которых уменьшается с ростом z.

§2. Предел и непрерывность функции многих переменных.

Для функций многих переменных определяются те же понятия, что и для функции одной переменной. Например, можно дать определения предела и непрерывности функции.

Опр. Число А называется пределом функции двух переменных z=f(x,y) при , и обозначается , если для любого положительного числа найдется положительное число , такое, что если точка удалена от точки на расстояние меньше , то величины f(x,y) и А отличаются меньше чем на .

Опр. Если функция z=f(x,y) определена в точке и имеет в этой точке предел, равный значению функции , то она называется непрерывной в данной точке.

Пример.

.

.

§3. Частные производные функции многих переменных.

Рассмотрим функцию двух переменных .

Зафиксируем значение одного из ее аргументов, например , положив . Тогда функция есть функция одной переменной . Пусть она имеет производную в точке :

.

Данная производная называется частной производной (или частной производной первого порядка) функции по в точке и обозначается: ; ; ; .

Разность называется частным приращением по и обозначается :

.

Учитывая приведенные обозначения, можно записать

.

Аналогично определяется

.

Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения частного приращения функции к приращению соответствующей независимой переменной, когда это приращение стремится к нулю.

При нахождении частной производной по какому-либо аргументу другие аргументы считаются постоянными. Все правила и формулы дифференцирования функций одной переменной справедливы для частных производных функции многих переменных.

Заметим, что частные производные функции являются функциями тех же переменных. Эти функции, в свою очередь, могут иметь частные производные, которые называются вторыми частными производными (или частными производными второго порядка) исходной функции.

Например, функция имеет четыре частных производных второго порядка, которые обозначаются следующим образом:

; ;

; .

и - смешанные частные производные.

Пример. Найти частные производные второго порядка для функции

.

Решение. , .

, .

, .

Задание.

1. Найти частные производные второго порядка для функций

, ;

2. Для функции доказать, что .

Полный дифференциал функции многих переменных.

При одновременном изменении величин х и у функция изменится на величину , называемую полным приращением функции z в точке . Так же, как и в случае функции одной переменной, возникает задача о приближенной замене приращения на линейную функцию от и . Роль линейного приближения выполняет полный дифференциал функции:

Полный дифференциал второго порядка:

=

= .

= .

В общем виде полный дифференциал п-го порядка имеет вид:

Производная по направлению. Градиент.

Пусть функция z=f(x,y) определена в некоторой окрестности точки M(x,y) и - некоторое направление, задаваемое единичным вектором . Координаты единичного вектора выражаются через косинусы углов, образуемых вектором и осями координат и называемых направляющими косинусами:

,

.

При перемещении точки M(x,y) в данном направлении l в точку функция z получит приращение

,

называемое приращением функции в данном направлении l.

Е сли ММ₁=∆l, то

.

Т

огда

.

О

пр. Производной функции z=f(x,y) по направлению называется предел отношения приращения функции в этом направлении к величине перемещения ∆l при стремлении последней к нулю:

.

Производная по направлению характеризует скорость изменения функции в данном направлении. Очевидно, что частные производные и представляют собой производные по направлениям, параллельным осям Ox и Oy. Нетрудно показать, что

.

Пример. Вычислить производную функции в точке (1;1) по направлению .

Опр. Градиентом функции z=f(x,y) называется вектор с координатами, равными частным производным:

.

Рассмотрим скалярное произведение векторов и :

Легко видеть, что , т.е. производная по направлению равна скалярному произведению градиента и единичного вектора направления .

Поскольку , то скалярное произведение максимально, когда векторы одинаково направлены. Таким образом, градиент функции в точке задает направление наискорейшего возрастания функции в этой точке, а модуль градиента равен максимальной скорости роста функции.

Зная градиент функции, можно локально строить линии уровня функции.

Теорема. Пусть задана дифференцируемая функция z=f(x,y) и в точке градиент функции не равен нулю: . Тогда градиент перпендикулярен линии уровня, проходящей через данную точку.

Таким образом, если, начиная с некоторой точки, строить в близких точках градиент функции и малую часть перпендикулярной ему линии уровня, то можно (с некоторой погрешностью) построить линии уровня.

Локальный экстремум функции двух переменных

Пусть функция определена и непрерывна в некоторой окрестности точки .

Опр. Точка называется точкой локального максимума функции , если существует такая окрестность точки , в которой для любой точки выполняется неравенство:

.

Аналогично вводится понятие локального минимума.

Теорема (необходимое условие локального экстремума).

Для того, чтобы дифференцируемая функция имела локальный экстремум в точке , необходимо, чтобы все ее частные производные первого порядка в этой точке были равны нулю:

Итак, точками возможного наличия экстремума являются те точки, в которых функция дифференцируема, а ее градиент равен 0: . Как и в случае функции одной переменной, такие точки называются стационарными.

Пример. .