5.3. Приложения двойного интеграла
Площадь S плоской области (S) вычисляется по формуле
или
.
(5.11)
Объём цилиндроида, ограниченного сверху непрерывной поверхностью z=f(x, y), снизу плоскостью z=0 и с боков прямой цилиндрической поверхностью, вырезающей на плоскости Оху область (S) (см. рис. 2), вычисляется по формуле
.
(5.12)
Площадь S гладкой поверхности z=z(x, y) выражается формулой
,
(5.13)
где (Р) – проекция данной поверхности на плоскость Оху.
Площадь S поверхности, заданной уравнением F(x, y, z)=0, выражается двойным интегралом:
,
где (Р) – проекция данной поверхности на плоскость Оху.
Если
(S)
– область плоскости Оху,
на
которой распределена масса с поверхностной
плотностью
,
то масса
m
этой
области
(пластинки)
определяется формулой
,
(5.14)
а
статические
моменты
и
относительно осей Ох и Оу –
формулами:
,
.
(5.15)
Если
-
центр тяжести пластинки, то
,
,
(5.16)
где m – масса пластинки; , - статические моменты относительно осей координат.
Если
пластинка однородна, т.е.
,
то формулы (5.16) принимают вид:
,
.
Моменты инерции пластинки (S) относительно осей Ох и Оу выражаются соответственно формулами:
,
,
(5.17)
а её момент инерции относительно начала координат – формулой
.
(5.18)
6. Тройной интеграл
Рассмотрим
замкнутую пространственную область
(V)
и функцию f(x,
y,
z),
определённую в этой области. Область
(V)
разобьём произвольным способом на n
элементарных областей
диаметрами
и объёмами
.
Наибольший из диаметров обозначим
буквой d.
В каждой элементарной области
выберем произвольно одну точку
и составим произведение
.
Интегральной
суммой для
функции f(x,
y,
z)
по области (V)
называется сумма вида
.
Тройным
интегралом от
функции f(x,
y,
z)
по области (V)
называется конечный предел интегральной
суммы при
:
.
Если функция f(x, y, z) непрерывна в области (V), то указанный предел существует и конечен (он не зависит от способа разбиения области (V) на элементарные области и выбора точек ).
Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.
В прямоугольных декартовых координатах тройной интеграл обычно записывается в виде
.
6.1. Вычисление тройного интеграла
Если
область интегрирования (V)
определяется неравенствами:
,
,
,
где
,
- непрерывные функции своих аргументов,
то тройной интеграл вычисляется по
формуле:
.
(6.1)
Область
(V)
ограничена сверху поверхностью
,
снизу поверхностью
,
а с боков цилиндрической поверхностью
с образующими, параллельными оси Oz,
вырезающей из плоскости Оху область
,
определённую неравенствами
,
(рис. 1).
Отметим, что порядок интегрирования может быть изменён. Тройной интеграл вычисляется шестью различными способами: в формуле (6.1) первое интегрирование совершается по z, второе – по у, третье – по х; сохранив первое интегрирование по z, можно поменять местами второе и третье; далее, в первую очередь можно выполнить интегрирование по х, а также по у.
В
частном случае, если функции
,
являются постоянными
,
,
то область интегрирования представляет
собой прямоугольный параллелепипед, и
формула (6.1) принимает вид:
.
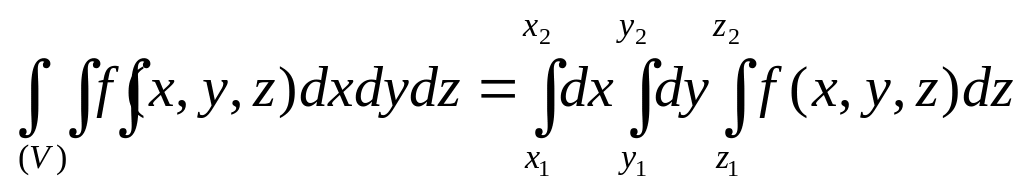Если
ограниченная замкнутая область (V)
пространства Oxyz
взаимно однозначно отображается на
область
пространства
с помощью непрерывно дифференцируемых
функций x=x(u,
v,
w),
y=y(u,
v,
w),
z=z(u,
v,
w)
и якобиан
(6.2)
в
области
не обращается в нуль, т.е.
,
то замена переменных в тройном интеграле
осуществляется по формуле
.
(6.3)
В
частности, при переходе от декартовых
координат x,
y,
z
к цилиндрическим
координатам
(рис. 2), связанным с x,
y,
z
формулами:
,
,
,
,
,
якобиан преобразования
,
поэтому
.
(6.4)
При
переходе от декартовых координат x,
y,
z
к сферическим
координатам
(рис. 3), связанным с x,
y,
z
формулами:
,
,
,
,
,
якобиан преобразования
,
и формула (6.3) принимает вид:
.
(6.5)