4.2. Определение параметров эмпирических формул методом наименьших квадратов в случае квадратичной зависимости величин

В результате измерений двух зависимых величин х и у получена следующая таблица их значений:

х				…
у				…

Будем рассматривать и как прямоугольные декартовы координаты точек на плоскости: , , …, . Допустим, что эти точки расположены почти на некоторой параболе. Естественно в этом случае предположить, что между х и у существует квадратичная зависимость, т.е.

, (4.6)

где a, b, с – некоторые постоянные коэффициенты (параметры), подлежащие определению.

Если в правую часть формулы вместо х подставить его значения из данной таблицы, то получим числа .

Было бы идеально подобрать параметры a, b, с так, чтобы при всех i выполнялось равенство . Однако при n>3 этого обычно сделать не удаётся, так как значения a, b, с, найденные из уравнений

, , ,

как правило, не удовлетворяют уравнениям

, …, .

Другими словами, , где - некоторые числа, называемые погрешностями.

Параметры формулы (4.6) выберем так, чтобы сумма квадратов погрешностей

была наименьшей. Для этого необходимо, чтобы выполнялись условия: , , . Находя частные производные функции u по a, b, с, приравнивая их к нулю, получаем так называемую нормальную систему:

(4.7)

Из системы (4.7) определяются параметры a, b, с эмпирической формулы (4.6).

Глава 2. Интегральное исчисление функций нескольких переменных

5. Двойной интеграл

На плоскости Оху рассмотрим область (S) площадью S, ограниченную замкнутой кривой (рис. 1). Пусть в этой области определена функция z=f(x, y). Разобьём область (S) сеткой линий на конечное число областей , площади которых соответственно. В каждой i-ой элементарной области выберем произвольно одну точку , значение функции в этой точке умножим на величину площади соответствующей области и все произведения сложим.

а). б).

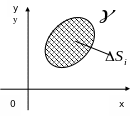
Рисунок 1

Полученная сумма

называется интегральной суммой функции f(x, y) в области (S).

Двойным интегралом от функции f(x, y) по области (S) называется конечный предел I интегральной суммы при , где - наибольший из диаметров элементарных областей :

.

Обозначения двойного интеграла:

, .

Функция z=f(x, y), для которой предел интегральной суммы существует и конечен, называется интегрируемой.

Если функция z=f(x, y) непрерывна в области (S), то она является интегрируемой в этой области.

Геометрический смысл двойного интеграла: если , то двойной интеграл от функции z=f(x, y) по области (S) равен объёму тела, ограниченного сверху поверхностью

z=f(x, y), снизу плоскостью z=0, с боков

цилиндрической поверхностью, образующие

которой параллельны оси Оz, а

направляющей служит контур

фигуры (S) (рис. 2).

Механический смысл двойного интеграла:

двойной интеграл от функции z=f(x, y)>0 по области

(S) представляет собой массу фигуры (S), если

подынтегральную функцию f(x, y) считать плотностью Рисунок 2

этой фигуры в точке М(х, у).

Свойства двойного интеграла:

1) ;

2) ;

3) если , то ;

4) ;

5) , где - области, на которые разбита область (S);

6) если в области (S) , то

, откуда

.