2.1. Частные производные и полный дифференциал функции нескольких переменных
Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее стремится к нулю.
Для функции двух переменных z=f(x, y), по определению, имеем:
(частная
производная по х);
(частная
производная по y).
При нахождении частной производной пользуются правилами дифференцирования функции одной переменной, считая все другие аргументы постоянными.
Если полное приращение функции z=f(x, y) в точке представимо в виде
,
где
P,
Q
– постоянные;
;
при
,
то
называют полным
дифференциалом
данной функции в этой точке и обозначают
через
:
.
Следовательно,
,
при
.
(2.1)
Функция,
обладающая непрерывными частными
производными, имеет полный дифференциал,
причём
,
.
Дифференциалы независимых переменных
совпадают с их приращениями, т.е.
,
.
Полный дифференциал функции z=f(x, y) вычисляется по формуле
.
Функция, имеющая полный дифференциал, называется дифференцируемой.
Из
формулы (2.1) следует, что
,
или
,
откуда
.
Полный дифференциал функции трёх переменных определяется аналогично и вычисляется по формуле
.
(2.2)
2.2. Производные и дифференциалы высших порядков
Частными производными второго порядка функции z=f(x, y) называются частные производные от её частных производных первого порядка:
,
,
,
.
Используются и другие обозначения:
,
,
,
,
,
,
,
.
Если
смешанные производные
,
непрерывны, то результаты дифференцирования
и
не зависят от порядка дифференцирования,
т.е.
= . (2.3)
Аналогично определяются частные производные второго порядка от функции трёх и более переменных, а также производные третьего и высших порядков.
Полным дифференциалом второго порядка функции z=f(x, y) называется дифференциал от её полного дифференциала:
.
Полные дифференциалы более высоких порядков определяются аналогично:
,
и т.д.
2.3. Дифференцирование неявных и сложных функций
Функция u от n переменных называется неявной, если она задана уравнением
,
(2.4)
не разрешённым относительно u.
Частные производные неявной функции, заданной уравнением (2.4), определяются формулами:
,
,
…,
.
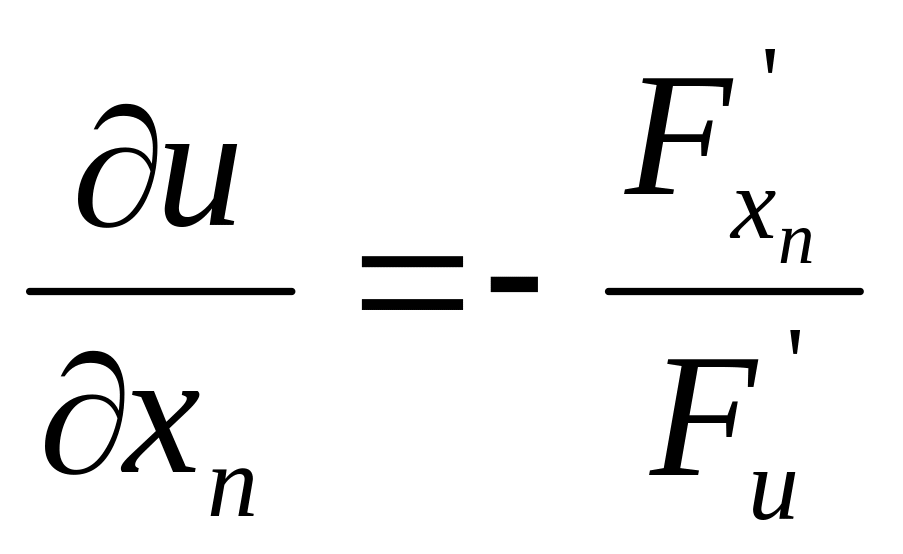В частности, если у – функция одной переменной х, заданная уравнением F(x, y)=0, то
;
(2.5)
если z – функция двух переменных х, у, заданная уравнением F(x, y, z)=0, то
,
.
Если
,
где
,
,
…,
,
то функция u
называется сложной
функцией независимых переменных
.
Переменные
называются промежуточными
аргументами.
Частная производная сложной функции по одной из независимых переменных равна сумме произведений частных производных по промежуточным аргументам и частных производных этих аргументов по данной независимой переменной:
(2.6)
Если все промежуточные аргументы являются функциями одной независимой переменной t, то функция (2.4) будет сложной функцией от t. Полная производная этой функции находится по формуле:
.