ГЛАВА 2. МОДЕЛИРОВАНИЕ И ИДЕНТИФИКАЦИЯ ПРОЦЕССОВ И СИСТЕМ

Практическая значимость рассмотренных в первой главе методов теории систем, системных исследований, системного подхода, системного анализа заключается в создании и использовании моделей систем. Часто говорят, что теория систем – это фактически теория моделей систем, и это верно, поскольку любая деятельность человека, исследователя становится возможной благодаря моделям систем и использованию их в практической деятельности.

Однако качество и эффективность модели, возможность и успех ее использования в задачах управления и принятия решений определяется успехом решения задачи идентификации. Именно проблема идентификации занимает исключительно важную роль, поскольку является в настоящее время наиболее «узким местом» при проектировании наукоемких и интеллектуальных систем управления и принятии решений

вусловиях неопределенности [17–21].

Вэтой связи в данной главе в едином контексте рассматриваются модели процессов и систем и методы их идентификации, что в настоящее время является наиболее конструктивным подходом при решении задач управления и принятия решений.

2.1. Моделированиеиидентификациясистем

Понятие«модельсистемы»

Понятие «модель системы», выполняющей роль посредника между исследователем и средой, играет важную роль в проведении системных исследований. Модель есть средство осуществления любой деятельности субъекта (исследователя, ЛПР). Под моделью обычно понимается некий объект-заместитель, который в определенных условиях может заменять объект-оригинал, воспроизводя интересующие субъекта свойства и характеристики оригинала, имеющий существенное преимущество перед оригиналом [1–3].

Имеются два типа средств, из которых могут создаваться модели: материальные средства и средства мышления. В этой связи признано, что моделями могут служить не только реальные объекты, но и абстрактные, идеальные построения, типичным примером которых служат математические модели, которые принято классифицировать как:

37

1)статические;

2)динамические;

3)линейные;

4)нелинейные;

5)непрерывные;

6)дискретные;

7)детерминированные;

8)стохастические;

9)параметрические;

10)непараметрические.

Обычно используются комбинированные модели объектов исследования и управления, которые обладают рядом различных признаков. Например, статические и динамические модели могут быть линейными либо нелинейными, дискретными либо непрерывными, детерминированными либо стохастическими.

Принципиально различный характер в подходе к построению моделей имеют детерминированные, вероятностные, статические и динамические модели.

Детерминированные модели описывают поведение систем в условиях полной определенности состояний системы в настоящем и будущем.

Вероятностные модели описывают поведение системы в условиях воздействия на систему случайных неконтролируемых факторов, а также случайных переменных внутреннего состояния системы. Вероятностные модели дают возможность оценивать будущие состояния системы, с учетом действия случайных неконтролируемых факторов, с известными вероятностно-статистическими характеристиками. Широкое применение математических моделей в задачах системных исследований и управления обусловлено универсальностью подхода, способностью отразить всё разнообразие закономерностей исследуемых процессов, сокращением затрат по сравнению с аналогичными исследованиями на реальных объектах, а также принципиальной невозможностью проведения натурных исследований на ряде важных объектов.

Сложные динамические системы характеризуются выполняемыми процессами (функциями), структурой и поведением во времени. Для адекватного моделирования таких систем различают функциональные, информационные и поведенческие модели, пересекающиеся друг с другом. Функциональная модель системы описывает совокупность выполняемых системой функций, характеризует морфологию системы (ее построение) – состав функциональных подсистем, их взаимосвязи. Информационная модель отражает отношения между элементами системы в виде структур данных (состав и взаимосвязи). Поведенческая (событийная)

38

модель описывает информационные процессы (динамику функционирования), в ней фигурируют такие категории, как состояние системы, событие, переход из одного состояния в другое, условия перехода, последовательность событий.

Следует упомянуть основные области применения моделей, такие как обучение, научные исследования и управление. При обучении с помощью моделей достигается высокая наглядность отображения различных объектов и облегчается передача знаний о них. Это в основном модели, позволяющие описать и объяснить систему. В научных исследованиях модели служат средством получения, фиксирования и упорядочения новой информации, обеспечивая развитие теории и практики. В управлении модели используются для обоснования решений. Такие модели должны обеспечить как описание, так и объяснение, и предсказание поведения систем.

Создание модели требует соответствующей квалификации, знаний, опыта, четких представлений о моделируемых системах и процессах, закономерностях их поведения и факторов внешней среды. Особенность построения математической модели состоит в том, что реальная система упрощается, схематизируется и описывается с помощью того или иного математического аппарата. Имеют место следующие основные этапы построения моделей [1–3, 7, 20]:

1)содержательное описание моделируемого объекта;

2)формализация операций;

3)проверка адекватности и качества модели;

4)корректировка модели;

5)оптимизация модели.

На этапе содержательного описания объекты моделирования представляются с позиций системного подхода. В соответствии с целью исследования устанавливаются необходимая совокупность элементов, взаимосвязи между элементами, возможные состояния каждого элемента, существенные характеристики состояний и соотношения между ними. На этом этапе моделирования широко применяются качественные методы описания систем, знаковые и языковые модели.

Этап формализации операций сводится к содержательному описанию исходного множества характеристик системы. После выделения главных и исключения несущественных характеристик выделяют управляемые и неуправляемые параметры и производят символизацию. Затем определяется система ограничений на значения управляемых параметров. Дальнейшие действия связаны с формированием вектора показателей качества модели, составленного из частных показателей качества (показатели исхода операции, целевой функции, полезности и т. п.).

39

На этапе проверки адекватности и качества модели предварительно необходимо уточнить, все ли существенные параметры включены в модель, нет ли в м одели несущественных параметров (вопросы избыточности модели), верно ли отражены функциональные связи между параметрами и ограничения на значения параметров. Для выявления слабых сторон модели целесообразно привлекать экспертов, которые не принимали участия в разработке модели, что позволяет выявить грубые ошибки.

После этого целесообразно приступить к реализации модели и проведению исследований для установления соответствия создаваемой модели оригиналу, а именно сравнение результатов моделирования с отдельными экспериментальными результатами, полученными при одинаковых условиях, использование других близких моделей, сопоставление структуры и функционирования модели с прототипом.

Главным критерием проверки адекватности и качества модели исследуемому объекту выступает практика. Однако процедура проверки адекватности и качества модели требует соответствующих экспериментальных данных, статистики, объем которых не всегда бывает достаточным для получения надежных результатов. По результатам проверки модели на адекватность принимается решение о возможности ее практического использования или о проведении корректировки.

На этапе корректировки модели могут уточняться структура и существенные параметры модели, ограничения на значения управляемых параметров, показателей качества и эффективности. После внесения изменений в модель осуществляется возврат к этапу проверки адекватности и качества модели.

На этапе оптимизации модели осуществляется ее упрощение при заданном либо допустимом уровне потери ее качества и эффективности. Основными показателями оптимизации являются факторы времени и затрат. В основе оптимизации лежит возможность преобразования моделей; преобразование выполняется с использованием математических методов либо эвристическим путем.

Теорияизадачиидентификациисистем

Теория и практика идентификации систем имеет длительную историю развития: вначале идентификация систем развивалась в рамках кибернетики – науки об управлении сложными динамическими системами, затем рассматривалась как раздел теории управления, а в настоящее время идентификация процессов и систем выступает как самостоятельное научное направление системных исследований [17].

40

Следует отметить, что идентификация как направление системных исследований представляет наиболее конструктивный подход к решению задач проектирования наукоемких и интеллектуальных систем управления и принятия решений в условиях неопределенности.

Задачей идентификации систем, или просто идентификации, является построение оптимальной (в смысле заданных критериев качества) математической модели системы по результатам измерений входных и выходных переменных, т. е. построение формализованного математического представления системы.

Задачи идентификации принято различать в узком и широком смысле. В узком смысле задача идентификации состоит в оценивании параметров и состояния системы по результатам наблюдений над входными и выходными переменными. При этом известна структура системы и задан класс моделей, к которому данная система относится. При идентификации в широком смысле решаются такие задачи, как выбор структуры системы и задание класса моделей, оценивание степени стационарности и линейности системы, выбор информативных переменных и т. д.

Разработанные в 50–70 гг. XX в. методы идентификации, как в узком, так и широком смысле (здесь часто используют термины параметриче-

ская и структурная идентификация), основаны на методах математи-

ческой статистики, теории статистических решений, математических методах оптимизации. В настоящее время широко известны классические методы идентификации: метод наименьших квадратов, максимального правдоподобия, метод стохастической аппроксимации и т. д. [17, 20–22, 25–27].

Однако использование классических методов идентификации при решении практических задач часто связано с проблемой устойчивости решений. Действительно, в реальных условиях функционирования стохастических объектов исходная информация о модели объекта, статистических характеристиках помех, как правило, неточная, и в распоряжении исследователя имеется ограниченный набор экспериментальных данных, заданный в виде одной ограниченной реализации процесса. В данных условиях приведенные выше классические методы идентификации часто оказываются неустойчивыми и неработоспособными.

В этой связи в 60–90 гг. XX в. интенсивное развитие получили методы устойчивого (робастного) оценивания и идентификации систем, основанные на использовании различной дополнительной априорной информации о решении, статистических характеристиках помех и т. п. Наиболее известные устойчивые (стабильные) алгоритмы идентификации сводятся, по существу, к вероятностно-статистическим методам

41

(робастный метод максимального правдоподобия, метод максимума апостериорной вероятности, Байесовские методы и т. п.), методам решения некорректных задач Тихонова, методам условной оптимизации при наличии ограничений [30–32].

Разработаны и интенсивно разрабатываются в настоящее время методы идентификации в условиях непараметрической априорной неопределенности, опираясь на представлении процессов и систем в виде «черного ящика», когда исследователь располагает лишь общими сведениями о их структуре, такими, как ограниченность функций, их гладкость, существование производных, существование решений на интервалах и т. д. [23, 24, 28, 29, 33]. Здесь наиболее известными методами являются:

1)непараметрические методы идентификации регрессионного типа, основанные на непараметрических оценках плотности вероятности;

2)нейросетевые алгоритмы идентификации на основе искусственных нейронных сетей (наборах взаимодействующих преобразователей информации – нейронов);

3)нечеткие алгоритмы идентификации, основанные на нечетких множествах Л. Заде и дающие более широкие возможности их практического использования по сравнению с вероятностно-статистическим подходом.

В настоящее время возникло понимание важности интеграции разнородной информации, понимание того, что, наряду с моделями исследуемых объектов, должны существовать и находиться с ними во взаимодействии модели, представляющие накопленные знания, описывающие поведение аналогичных объектов, а также разнообразные дополнительные данные.

Понимание необходимости интеграции разнообразной информации

взадачах идентификации и управления сложными процессами и системами привело к созданию интегрированных моделей и системы идентификации, состоящих из согласованных моделей компонент, что позволило воспроизводить целостные, системные свойства реальных объектов и существенно повышать качество процедур идентификации, управления и принятия решений в условиях неопределенности [17, 18]. Важной компонентой интегрированной системы являются формализованные модели, учитывающие дополнительную априорную информацию, накопленный опыт и знания ЛПР.

Ценность интегрированных моделей и системы идентификации заключается в том, что они обеспечивают системное решение актуальных задач [17], а именно:

42

1) создание эффективных процедур учета разнородной дополнительной априорной информации, обеспечивающих согласованность исходных, дополнительных априорных данных, накопленного опыта

изнаний;

2)обеспечение устойчивости решений;

3)повышение помехоустойчивости и точности алгоритмов принятия решений при малом объеме исходных данных;

4)оптимизация решений прикладных задач идентификации, управления и принятия решений.

2.2. Математическиемоделипроцессовисистем

Объекты моделирования и идентификации – технические, экономические или социальные системы – удобно формально представлять в виде многополюсника со многими входами и выходами [25, 26], где через X = (x1, x2 , ..., xn ) обозначены входы объекта, а через

Y = (y1, y2 , ..., ym ) – реакции объекта на входные возмущения (рис. 2.1).

Рис. 2.1. Представление объекта и процесса идентификации

Входы объекта представляют собой воздействия внешней среды на объект и являются какими-то определенными функциями состояния среды и времени. Поскольку состояние среды никогда точно не известно, то входы и выходы объекта естественно рассматривать как случайные функции времени, статистические свойства которых в общем случае неизвестны. Однако обычно известны наблюдения входа и выхода, т. е. реализация функций X * (t) и Y * (t).

Объект связывает входы X*с его выходом Y*. Эту связь формально можно охарактеризовать некоторым оператором F0, таким, что

где ξ – неконтролируемые источники случайных возмущений. Поэтому под моделью объекта естественно также понимать неко-

торый оператор F, который преобразует наблюдаемое входное воздействие на объект X в его реакцию Y = F(X). При классическом подходе задача идентификации заключается в построении модельного оператора F из некоторого класса операторов по наблюдениям X* и Y*, который

43

был бы близок к F0 в смысле некоторого критерия оптимальности. Рассмотрим некоторые примеры видов операторов F и соответствующие им модели, наиболее часто используемые при решении практических задач, в т. ч. и задач идентификации и управления процессами нефтегазодобычи. Более детальные перечень и описание видов операторов и моделей объектов идентификации приведены в научных работах

[10, 15, 17–19, 20–22].

Статическиемодели

1. Линейные детерминированные модели. Модель линейного стати-

ческого объекта с n входами и m выходами описывается системой линейных алгебраических уравнений

j=1

или в векторной форме Y = AX , где Y = (y1, y2 ,..., yn )T – вектор-столбец

выходных переменных объекта в момент времени t; X = (x1, x2 ,..., xm )T – вектор-столбец входных переменных объекта в момент времени t; A = (αij , i = 1, n, j = 1, m) – матрица коэффициентов.

Задача идентификации системы (2.2) состоит в оценивании матрицы коэффициентов A.

2. Нелинейные параметрические модели (функции регрессии). Мо-

дель объекта в этом случае представляем в виде известной функции с неизвестными параметрами

где у – выходная переменная объекта; f (x,α) – известная функция двух векторных аргументов x = (x1, x2 , …, xm ) – входа объекта и вектора не-

известных параметров α = (α1, α2 , …, αm ).

Задача идентификации сводится к определению параметров α на основе экспериментальных наблюдений.

Частным случаем параметрических моделей являются модели, линейные относительно оцениваемых параметров. Такие модели образуются в результате разложения искомой функции по заданной системе

k

функций f (x,α) = ∑α jϕ j (x), где ϕ j (x) – система векторных линейно

j=1

независимых функций. Частным случаем такого представления является аппроксимация функции f (x,α) отрезком многомерного ряда Тейлора.

44

Отметим преимущества использования нелинейных моделей объектов:

1)нелинейность является существенным свойством большинства реальных объектов;

2)дополнительная информация часто позволяет выбрать достаточно точную нелинейную модель с числом параметров значи-

тельно меньше, чем для аналогичной линейной модели. Приведем примеры практического использования нелинейной рег-

рессионной модели объекта.

3. Модель производственных функций

y = f (x,α) = α0 x1α1 x2α2 ,..., xmαm ,

где y – результат производства (объем дохода); x1, x2 , …, xm – затраты, факторы производства (капитала, труда, информации, технологии ит. д.).

Параметры α1, α2 , …, αm отражают влияние факторов x1 , x2 ,..., xm на результат y.

4. Функция регрессии в задаче медицинской диагностики

f(t,α) = α1 + α2 exp(−α4t).

α3

Данная функция описывает изменение содержания сахара в плазме крови человека после «нагрузки» глюкозой. Используется в алгоритмах ранней диагностики заболеваний сахарным диабетом.

5. Функция регрессии в задаче интерпретации гидродинамических исследований скважин нефтяного месторождения

f (t,α) = α + α ln(α t + α ) .

1 2 3 4

Данная функция описывает изменение забойного давления нефтяных скважин после их остановки в целях определения фильтрационных параметров нефтяной залежи.

6. Функция регрессии в задачах прогноза добычи нефти и оценки извлекаемых запасов

f (t,α) = α1tα2 exp(−α3t ).

Данная зависимость является простой моделью, отражающей изменение добычи нефти в процессе разработки нефтяного месторождения. Используется для прогноза добычи нефти и оценки извлекаемых запа-

сов флюидов [17]: S = T∫ f (t,α)dt, где Т – время окончания разработки

0

нефтяного месторождения.

45

7. Статические стохастические модели. Статический стохастиче-

ский объект в общем случае описывается функцией вида

где F – оператор объекта, ξ – случайные неконтролируемые факторы (помехи), порожденные либо самим объектом, либо средствами сбора и передачи информации.

Обычно предполагается, что помехи аддитивные, т. е. регулярная и случайная составляющая выхода могут быть разделены:

Статистические свойства случайной составляющей ξ в общем случае зависят от контролируемого входа X. Модель объекта часто представляется в виде нелинейной многомерной функции регрессии вида

которая не зависит от неконтролируемой случайной составляющей ξ.

8. Непараметрические стохастические модели. Непараметриче-

ские статические стохастические модели описываются функцией, относительно которой известны лишь достаточно общие сведения, такие как непрерывность, ограниченность, существование производных и т. д. При данных априорных предположениях в качестве модели объекта часто используют функцию регрессии (условное математическое ожидание)

где P( y / x) – условная плотность вероятности выхода объекта.

Задача идентификации в данном случае заключается в оценке условной плотности вероятности и функции регрессии на основе наблюдений входа и выходов объекта.

Динамическиемодели

В качестве математического описания динамических объектов наиболее часто используют интегральные уравнения, обыкновенные дифференциальные уравнения, дифференциальные уравнения в частных производных, конечно-разностные, дискретные аналоги интегральных

идифференциальных уравнений:

1.Динамические системы на основе интегральных уравнений.

Модель линейного динамического объекта, на вход которого поступает

сигнал x(t) , вызывающий реакцию y(t), часто представляют в виде интегрального уравнения

46

Задача идентификации заключается в определении импульсной переходной функции (ИПФ) объекта h(t,τ) либо h(τ).

Наряду с описанием линейного объекта с помощью ИПФ можно использовать его описание с помощью передаточной функции ϕ(t, p),

связанной с ИПФ соотношениями

В стационарном случае ϕ(t, p) = ϕ(t − p).

Модель нелинейного динамического инерционного объекта строится в предположении, что нелинейность и инерционность объекта можно разделить и представить объект в виде последовательной комбинации двух звеньев: нелинейного безынерционного и динамического линейного. В одномерном случае, предполагая, что инерционное звено

стационарно, выход объекта y(t) связан с его входом x(t) одним из двух соотношений:

Задача идентификации будет состоять в определении пары функций: h(t) и f (t).

2. Динамические системы, описываемые обыкновенными диффе-

ренциальными уравнениями. Модель линейного динамического объекта,

n и m – параметры структуры (порядок) уравнения.

47

Если система нестационарная, то коэффициенты уравнения ai и bi должны быть функциями времени. Задача идентификации заключается

вопределении порядка уравнения, коэффициентов ai, bi и начальных состояний (если они неизвестны).

Класс моделей на основе интегральных и обыкновенных дифференциальных уравнений имеет свои преимущества и недостатки. Модели на основе дифференциальных уравнений могут приводить к большим ошибкам идентификации, если порядок модели не соответствует порядку объекта. Преимущество моделей на основе интегральных уравнений состоит в том, что они не требуют явного знания порядка объекта. Однако в этом случае описание объекта является непараметрическим, бесконечномерным, поскольку определение функции эквивалентно определению (заданию) бесчисленного числа параметров.

3.Нелинейные динамические модели. В непрерывном случае одно-

мерный динамический объект (один вход и один выход) может быть

впростейшем случае описан с помощью нелинейного дифференциального уравнения

где f – нелинейная функция n + m +1 аргумента, которую и нужно идентифицировать.

4. Динамические системы, описываемые дифференциальными уравнениями в частных производных. Динамические объекты, представ-

ленные дифференциальными уравнениями в частных производных, имеют чрезвычайно широкое научное и практическое применение при решении разнообразных задач гидротермодинамики, переноса излучения, прогноза погоды, динамики атмосферы и океана и т. д.

Дифференциальное уравнение с частными производными порядка r есть функциональное уравнение вида

содержащее по меньшей мере одну частную производную порядка r от неизвестной функции f ( X ) , где X = (x1, x2 , …, xn ).

В качестве примера рассмотрим дифференциальное уравнение параболического типа однофазной фильтрации, которое описывает плоскорадиальный приток сжимаемой жидкости к скважине нефтяного пласта,

∂P = ∂P + ∂2 P2 ,

χ∂t r∂r r∂r

48

где P – давление в момент времени t на расстоянии r от оси скважины; χ – коэффициент пьезопроводности пласта, который характеризует скорость перераспределения давления в пласте.

Задача идентификации заключается в определении пьезопроводности пласта по результатам гидродинамических исследований скважины

ирегистрации кривой изменения давления после остановки скважины.

5.Дискретные, конечно-разностные аналоги интегральных и диф-

ференциальных уравнений. При решении задач идентификации широкое

применение получили дискретные, конечно-разностные аналоги интегральных и дифференциальных уравнений с использованием численных методов.

Суть этих методов заключается в замене интегралов суммами, а производных – их конечными разностями. Это позволяет свести интегральные и дифференциальные уравнения к соответствующим системам сеточных алгебраических уравнений. Решение уравнений определяется в узлах сетки, что часто требует запоминания большого объема данных

ипроведения больших вычислений.

2.3.Методыидентификациисистем вусловияхнеполнойинформации

Рассмотрение методов идентификации систем в условиях неполной информации начнем с изложения основных классических методов идентификации статических объектов максимального правдоподобия и наименьших квадратов.

Постановказадачиидентификациистатическихобъектов

Пусть имеется модель статического стохастического объекта вида y = f (x,α) + ξ,

где x = (x1, x2 , …, xm ) – вектор входных величин; α = (α1, α2 , …, αm ) – вектор параметров модели объекта; y – выходная величина; ξ – случайная неконтролируемая переменная, представляющая погрешности изме-

рений (помех), ошибки, связанные с выбором модели вида f (x,α) и па-

раметров и т. п. Здесь y R1, ξ R1, x Rm , α Rm определены в соответствующих областях евклидового пространства.

Требуется по измерениям выходной и входных переменных (yi*,

49

где f (xi ,α) – известная с точностью до вектора параметров функция.

будет использована и другая дополнительная априорная информация относительно плотности pξ (z)и параметрах модели α.

Систему моделей (2.3.1) удобно представить в матричной форме

столбцы значений выходной переменной, модели и случайных неконтролируемых факторов.

Методымаксимальногоправдоподобия инаименьшихквадратов

Предположим, что плотность распределения случайных величин pξ (z) известна, а априорная информация о решении полностью отсут-

ствует. Одним из наиболее распространенных методов идентификации в этой ситуации является метод максимального правдоподобия (ММП) [26, 27], который в данном случае принимает вид

В частности, если pξ (z) – плотность нормального распределения случайной величины ξ − N (0,σ2 )

pξ (z) = 2 1σ exp(−z2 / σ),

то ММП (2.3.3) переходит в метод наименьших квадратов (МНК):

а если pξ (z) – плотность распределения Лапласа – L(0,a)

pξ (z) = 21a exp(− z / a),

то из (2.3.3) получаем метод наименьших модулей (МНМ)

50

Отметим, что для простейшего случая f (x,α) = α = const оценка

(2.3.4) совпадает с выборочным средним:

α* = 1 ∑n yi*, n i=1

а оценка (2.3.5) – с выборочной медианой:

α* = med (y1*, …, yn* ).

Следует также отметить, что в случае линейного статического объекта, представленного по аналогии с (2.3.2) в матричной форме,

и сводится к решению системы линейных алгебраических уравнений (СЛУ)

Оценки максимального правдоподобия (2.3.3) при некоторых предположениях асимптотически несмещенные, состоятельные и оптимальны в том смысле, что их среднеквадратическая ошибка аппроксимации при объеме выборки n → ∞, достигает минимально возможного значения,

совпадающего с нижней границей неравенства Рао–Крамера [31, 32]

где M – символ математического ожидания; I ( p) – фишеровская информация. Предполагается, что I ( p) существует и конечна, а матрица Bn невырождена.

Оценки МНК (2.3.7)

обладают оптимальными свойствами при конечном объеме выборки n, и в классе линейных несмещенных оценок их дисперсия достигает

51

минимально возможного значения, что, в частности, обусловливает их широкое применение при решении практических задач.

Однако своеобразной «платой» за оптимальность оценок максимального правдоподобия и наименьших квадратов являются их неустойчивость, нестабильность при нарушении комплекса условий их нормального функционирования [17, 18, 27], а именно нормальности распределений вероятностей случайных факторов, ограниченность их дисперсий, отсутствие ошибок измерений входных переменных, невы-

рожденности матрицы FT F и т. п. Следует отметить, что обеспечить выполнение отмеченных выше условий нормального функционирования при решении многих задач идентификации и управлении процессами нефтегазодобычи в условиях неопределенности практически невозможно. Например, если плотность вероятности распределений помехи ξ равна

pξ (z) = (1− α) f (z) + αϕ(z),

где f (z) – гауссова плотность, ϕ(z) – плотность распределения с бес-

конечной дисперсией (модель, учитывающая выбросы, резко выделяющихся значения от основной массы наблюдений), то выборочное среднее имеет бесконечную дисперсию, а оценки (2.3.3), (2.3.4), (2.3.7) в этом случае не только не оптимальны, но даже не состоятельны, хотя функция распределения помехи близка к нормальному распределению

(0 < α ≤1).

Другим примером неустойчивости оценок ММП, МНК является

вырожденность либо плохая обусловленность матрицы FT F при малом объеме исходных данных n , когда размерность вектора оцениваемых параметров m > n. В данном случае определитель матрицы равен нулю, что нетрудно наглядно представить, если задача идентификации заключается в определении параметров уравнения прямой, проходящей через одну точку (n = 1, m = 2).

Устойчивыйметодмаксимальногоправдоподобия

Рассмотрим устойчивый метод максимального правдоподобия, предполагая, что известен лишь некоторый класс плотностей распределений вероятностей случайных факторов, помех P, p P [32]. В данном

случае, по аналогии с ММП, имеют место оптимальные приближения вектора неизвестных параметров

52

p* = arg min I ( p),

p P

где p* – наиболее благоприятное распределение из класса P, обеспечивающее минимально возможное значение фишеровской информации

классов распределений помех являются невырожденные распределения, распределения с ограниченной дисперсией, «приближенно нормальные» распределения, «приближенно равномерные» распределения ит. п.

Например, для класса всех невырожденных распределений наиболее благоприятное распределение p* совпадает с распределением Лапласа

ϕ* (z) = z и метод (2.3.9) совпадает с методом наименьших модулей (2.3.5). Для класса распределений с ограниченной дисперсиейϕ* (z) = z2 метод (2.3.9) сводится к методу наименьших квадратов.

МетодмаксимумаапостериорнойвероятностиБайеса

Используя априорную информацию о решении, в данном случае информацию о распределении pа (α) вектора параметров α и формулу

Байеса

p(α / y) = p(α, y() p) (α),

p y

нетрудно [по аналогии с оценками (2.3.3)] получить оценки метода мак-

i=1

Приведем для примера решение задачи (2.3.10) для линейного статического объекта (2.3.6), когда случайные величины ξ независимы,

имеют нормальное распределение N (0,σξ2 )с нулевым средним и дисперсией σξ2 , а случайные величины α независимы, имеют нормальные распределения N (α j ,σ2a ) со средними значениями Mα j = α j , j = 1,m

и дисперсией σ2a . В данном случае оценка метода максимума апостериорной вероятности (3.10) примет вид

53

где x 2 означает квадратичную норму вектора x, а βn = σξ . nσα

Нетрудно показать, что решение оптимизационной задачи по определению оптимальных оценок α* (2.3.11) сводится к решению системы линейных уравнений вида

Отметим, что при βn = h, α = 0 метод максимума апостериорной ве-

роятности приводит к решению регуляризованной по А.Н. Тихонову системы линейных уравнений с параметром регуляризации h, определение которого является самостоятельной задачей [30, 31].

Преимущество оценок (2.3.12) при конечных объемах данных n заключается в обеспечении невырожденности матрицы (FT F + βn I )

в случае вырожденности либо плохой обусловленности матрицы F T F. Недостатком оценок (2.3.12) является их смещенность при конечных объемах исходных данных.

МетодрегуляризациипоА.Н.Тихонову

Задача идентификации статического объекта (2.3.1) с использованием метода регуляризации А.Н. Тихонова заключается в решении оптимизационной задачи вида [30, 31]

сглаживающим, h – параметр регуляризации (сглаживания). Выбор стабилизирующего функционала Ω(α) определяется видом модели иссле-

дуемого объекта и наличием априорной информации о решении, «гладкости» решения, уклонении решения от начала координат и т. п.

Например, при Ω(α) = α 2 определение оптимальных значений параметра α* (h) для линейного статического объекта сводится к решению регуляризированной СЛУ вида

(FT F + hI )α* (h) = FT y*.

Нетрудно видеть, что при параметре регуляризации h = 0 оценка α* (0) совпадает c оптимальной оценкой МНК (2.3.8). Отметим, что при

h > 0 оценка α* (h) уже не обладает оптимальными свойствами, хотя

54

обеспечивает невырожденность матрицы (F T F + hI ), поскольку ее определитель не равен нулю: det t(FT F + hI ) ≠ 0.

При Ω(α) = α − α 2 определение оптимальных значений параметра

α* (h) для линейного статического объекта сводится к решению СЛУ вида

где α – априорная информация о решении. В данном случае оценка (2.3.14) при соответствующем выборе параметра регуляризации h совпадает с приближением метода максимума апостериорной вероятности Байеса при нормальном распределении ошибок измерений и нормальном распределении вектора случайных величин α с математическими

ожиданиями Mα = α (2.3.12).

Следует отметить, что между приведенными выше методами идентификации (ММП, МНК, МАВ), основанными на вероятностно статистическом подходе, и методом регуляризации по А.Н.Тихонову, основанном на функциональном подходе к решению некорректно поставленных задач, есть области «пересечения», области общих свойств оценок.

Непараметрическиеметодыидентификациисистем

в условиях непараметрической априорной неопределенности о структуре модели, когда о функции f (x) известны лишь общие свойства, такие

как однозначность, непрерывность, существование производных (мо-

ния входных и выходных переменных объекта x = (x1, x2 , …, xm ), i = 1,m с плотностью p(y, x) ξi – случайные величины с плотностью pξ (z).

Остановимся на статистическом подходе к идентификации объекта (2.3.15) с использованием функции регрессии r(x), которая, как извест-

но, является наилучшим приближением к модели объекта f (x)

55

P(y / x) = P(y, x) / P(x) – условная плотность распределения вероятно-

сти переменных y, x.

Задача идентификации статического стохастического объекта (2.3.15) заключается в оценке плотностей вероятности P(y, x), P(x)

и соответственно функции регрессии r(x).

Рассмотрим метод оценки функции регрессии с использованием непараметрических «ядерных» оценок плотности вероятности вида

[28, 29, 33]

hj , j = 1,m – параметры «сглаживания».

По аналогии с (2. 3.17) имеет место непараметрическая оценка совместной плотности вероятности P(y, x)случайных величин y, x

Подставляя оценки (2.3.17) и (2.3.19) в (2.3.16) и учитывая свойства ядер (2.3.18), получим непараметрическую «ядерную» оценку функции регрессии

Непараметрические оценки регрессии (2.3.20) широко используются в задачах идентификации, обработки экспериментальных данных в случаях, когда априорная информация о виде модели объекта отсутствует (модель «черного» ящика), когда известны лишь значения его входных и выходной переменных. В качестве ядер k, kj часто используют функции:

а) k (u) = exp(−u2 / 2);

56

асимптотическими оптимальными свойствами при бесконечно большом объеме выборки n (n → ∞). При конечных выборках непараметрические

оценки регрессии смещенные. Существуют различные методы устранения смещения непараметрических оценок регрессии, наиболее эффективными из которых являются метод «складного ножа» [29] и метод локальной аппроксимации плотности вероятности [34].

Другим интенсивно развивающимся в настоящее время методом идентификации систем в условиях непараметрической априорной неопределенности является подход, основанный на теории искусственных нейронных сетей (нейронах) [23]. Формально нейрон можно представить в виде системы

функционирующей в два такта. На первом такте вычисляется величина суммарного возбуждения y, полученная от входных сигналов xi, взвешенных с весами wi. На втором такте для получения выходного сигнала z суммарное возбуждение пропускается через монотонно неубывающую

функцию активации φ, удовлетворяющую условию ϕ(x) < 1. В качестве

функций активации часто используются зависимости: 1) пороговая функция

2) логистическая функция

3)гиперболический тангенс

ϕ(x) = th(αx), α > 0.

Нейрон (2.3.21) способен получать сигналы и выдавать выходной сигнал z, близкий к нулю либо единице. Если выходной сигнал близок либо равен единице, то нейрон возбужден.

57

Нейроны вида (2.3.21) могут быть объединены в нейронную сеть определенной топологии (сети прямого распространения– персептроны, сети радиально базисных функций – RBF-сети, самоорганизующие карты Кохонена, сети Хопфилда и т. д.) [23].

Рассмотрим для примера решение задачи идентификации статического стохастического объекта (2.3.15) с одним входом и одним выходом с использованием RBF-сети

mj – центры базисных функций; σj – регулирующий параметр. Задача идентификации в данном случае сводится к решению оптимизационной задачи

по определению параметров ω*ij , где {yin } – обучающий набор измере-

ний выходной переменной y.

Следует отметить, что приближение функции на основе RBF-сети, по сути, близко к непараметрическим оценкам функции регрессии (2.3.20). Например, при ωij = 1 и использовании в качестве базисных

функций с центрами mi = xi

оценки (2.3.23) и (2.3.20) при m = 1 совпадают.

2.4. Интегрированныесистемыидентификации

Актуальным, интенсивно развивающимся в настоящее время направлением в области идентификации является построение математических моделей систем с учетом разного рода дополнительной априорной информации, накопленного опыта и знаний, удобным описанием которых является понятие объекта-аналога, т. е. системы, подобной исследуемому объекту [17, 18].

Объединение модели исследуемого объекта и модели объектованалогов в виде некоторой интегрированной системы моделей позволя-

58

ет отразить целостные, системные свойства реальных объектов, что существенно расширяет возможности традиционных методов идентификации систем и области их практического применения.

Интегрированныесистемымоделей сучетомаприорнойинформации

Удобной моделью, позволяющей учитывать различные дополнительные апостериорные либо априорные данные, является понятие объект-аналога, т. е. система, подобная исследуемому объекту.

Объект-аналог определим как реально существующий либо воображаемый упрощенный объект, отражающий основные черты исследуемой системы, особенности его строения и функционирования, представляющий и формализующий в виде моделей дополнительные апостериорные и априорные данные, накопленный опыт и знания.

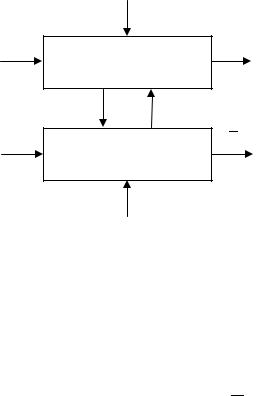
Объект-аналог Fa, изображенный на рис. 2.2, является некоторым отражением исследуемого объекта F (некоторый образ объекта управления либо его окружения)

ξt

Рис. 2.2. Представление объекта eghfdktybz и объекта аналога

Исследуемый объект и объект-аналог представляют некоторую интегрированную систему взаимодействующих моделей:

где Y*, U*, X* – реализации выходных Y, входных U, X, управляемых

и наблюдаемых переменных объекта управления; V t – вектор выходных переменных моделей объектов-аналогов, представляющих дополнительные априорные данные, экспертные оценки и т. д.; F, Fa – модели исследуемого объекта и объекта-аналога (функции, функционалы, а в общем

59

случае операторы); ξi, η – случайные величины, представляющие погрешности измерений переменных исследуемого объекта и объекта аналога, ошибки, связанные с выбором модели, действием случайных неучтенных факторов, и т. п. Переменные Z объекта-аналога могут соответствовать переменным объекта управления, а также представлять параметры, функции (функционалы). Оператор модели объекта-аналога Fa, как и оператор модели объекта управления F, может быть представлен классами статических, динамических, параметрических либо непараметрических моделей, рассмотренных в параграфе 2.2.

В качестве примера системы моделей (2.4.1) приведем интегрированную стохастическую систему моделей добычи нефти, основанную на регрессионной модели добычи нефти f (t, α)

аналогов, представляющих дополнительные априорные сведения и экспертные оценки извлекаемых запасов [17]:

где Q* (ti ), i = 1,n – фактические значения добычи нефти за соответствующие промежутки времени t = ti − ti−1, i = 1,n (год, месяц); Qн (ti ), i = 1,n – значения добычи нефти, полученные на основе модели f (t,α); νj , j = 1, p – дополнительные априорные данные и экспертные оценки

извлекаемых запасов нефти за время разработки месторождения T; νa (α)– извлекаемые запасы, полученные на основе модели добычи

нефти f (t,α).

Исследуемому объекту управления может соответствовать не один,

анесколько объектов-аналогов, изображенных на рис. 2.3.

Вэтом случае получим интегрированную систему моделей

V = F (t, Z , η ), j = 1,m.

j aj j j

Простым примером системы моделей (2.4.3) может быть интегрированная стохастическая система моделей дебита скважин на основе регрес-

сионной модели дебита скважин f (t, kпр, Pпл − Pз ) с учетом априорной информации о продуктивности скважины и пластовом давлении [25]:

60

и экспертные оценки продуктивности скважины kпр (ti ) и пластового

давления Pпл (ti ); νi, εi – случайные величины, представляющие ошибки дополнительных априорных сведений и экспертных оценок.

ξt

Рис. 2.3. Структура интегрированной системы моделей первого уровня

Другим примером интегрированной системы моделей (2.4.3) может быть система моделей производственной функции, с учетом экспертных оценок емкости рынка νj и прогнозных значений объемов реализован-

ной продукции ytn +τ на период времени τ,

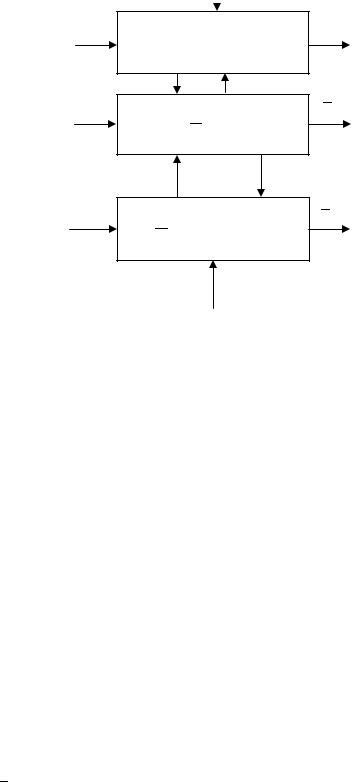
ции за соответствующие периоды времени t = ti − ti−1, i = 1,n. Объект-аналог первого уровня Fa1 (Z1 ) может, в свою очередь, иметь

свой аналог – Fa2 (Z1, Z2 ) и т. д. В данном случае имеет место много-

уровневая иерархическая интегрированная система моделей, приведенная на рис. 2.4:

61

Рис. 2.4. Представление многоуровневой интегрированной системы моделей

В этом случае получим интегрированную систему моделей

Примером (2.4.6) может быть интегрированная система добычи нефти нефтяного месторождения, разбитого на участки разработки [17]:

где Qн*j (ti ), v j – добыча нефти и экспертные оценки извлекаемых запасов участков разработки. В данном случае в качестве объекта аналога

62

второго уровня выступает экспертная оценка извлекаемых запасов V всего месторождения.

Многообразие интегрированных систем моделей определяется многообразием моделей исследуемых объектов и моделей объектованалогов. Введем следующую классификацию интегрированных систем моделей (ИСМ) объектов управления [17, 18]:

1)линейные ИСМ;

2)нелинейные ИСМ;

3)непараметрические ИСМ;

4)комбинированные ИСМ.

Линейные ИСМ. Линейные интегрированные системы моделей объектов управления основаны на линейных статических либо динамических моделях исследуемых объектов разработки и на линейных (статических либо динамических) моделях объектов-аналогов.

Нелинейные ИСМ. Нелинейные интегрированные системы моделей объектов управления основаны на нелинейных статических либо динамических моделях исследуемых объектов разработки и линейных либо нелинейных моделях объектов налогов.

Непараметрические ИСМ. Непараметрические интегрированные системы моделей ТПР основаны на непараметрических статических либо динамических моделях ТПР и на непараметрических статических либо динамических моделях априорной информации.

Непараметрические интегрированные системы моделей ТПР используются в случаях, когда объект разработки слабо изучен либо достаточно сложный для его описания на основе параметрической, физически содержательной модели фильтрации флюидов. С другой стороны, и объекты-аналоги, представляющие дополнительные априорные данные, и экспертные оценки не удается представить в виде конечномерного параметрического описания.

Комбинированные ИСМ. Наиболее распространенными в настоящее время моделями объектов управления, позволяющими интегрировать всю имеющуюся информацию, являются комбинированные интегрированные системы моделей. Комбинированные ИСМ представляют более широкий класс моделей, включающий в себя линейные, нелинейные, непараметрические статические либо динамические интегрированные системы моделей и их комбинации.

63

Основныепонятияинтегрированныхсистемидентификации

Под интегрированной системой идентификации будем понимать процесс создания (проектирования) оптимальной (в смысле заданных критериев качества) структуры интегрированной системы моделей

(2.4.1), (2.4.3), (2.4.6).

В общем виде оптимальную структуру интегрированной системы моделей можно представить в виде [17]

к решению задач структурной оптимизации по определению вида функ-

ций f (α), fa (α):

и задач параметрической оптимизации по определению оптимальных значений α* (β) параметров моделей:

где Φ – комбинированный показатель качества, составленный из частных показателей качества объекта управления и показателей объектованалогов. Комбинированный показатель качества часто выбирают в виде суммы частных показателей качества:

j=1

модели объекта управленияJ0 (α)и взвешенных с весами βj показателей качества моделей объектов аналогов Jaj (α). Выбор вида частных пока-

зателей качества определяется наличием априорной информации о ве- роятностно-статистических характеристиках помех, априорной информации о параметрах модели α.

Приведем для примера решение задачи параметрической идентификации по определению оптимальных значений параметров линейной интегрированной системы моделей

64