
Конспект урока по математике
.doc
ОТКРЫТЫЙ УРОК ПО ТЕМЕ
« ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА».
2 часа.
11 а класс с углубленным изучением математики
Проблемное изложение.
Проблемно – поисковые технологии обучения.
13 декабря 2000г.
ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
ЦЕЛЬ УРОКА :
- активизировать мыслительную деятельность;
- способствовать усвоению способов исследова-
ния;
- обеспечить более прочное усвоение знаний.
ЗАДАЧИ УРОКА:
-
ввести понятие первообразной;
-
доказать теорему о множестве первообразных для заданной функции (применяя определение первообразной);
-
ввести определение неопределенного интеграла;
-
доказать свойства неопределенного интеграла;
-
отработать навыки использования свойств неопределенного интеграла.
ПРЕДВАРИТЕЛЬНАЯ РАБОТА :
-
повторить правила и формулы дифференцирования
-
понятие дифференциала.
ХОД УРОКА
Предлагается решить задачи. Условия задач записаны на доске.
Учащиеся дают ответы по решению задач 1, 2.
(Актуализация опыта решения задач на использование дифферен-
цирования ).
1. Закон движения тела S(t) , найти его мгновенную
скорость в любой момент времени.
-
V(t)
= S![]() (t).
(t).
2. Зная, что количество электричества, протекающего
через
проводник выражается формулой q
(t)
= 3t![]() - 2 t,
- 2 t,
выведите формулу для вычисления силы тока в любой
момент времени t.
- I (t) = 6t - 2.
3 . Зная скорость движущегося тела в каждый момент вре-
мени, найти закон его движения.
-
Зная , что сила тока проходящего через проводник в лю-
бой момент времени I (t) = 6t – 2 , выведите формулу для
определения количества электричества, проходящего
через проводник.
Учитель : Возможно ли решить задачи № 3 и 4 используя
имеющиеся у нас средства ?
( Создание проблемной ситуации ).
Предположения учащихся :
- Для решения этой задачи необходимо ввести операцию,
обратную дифференцированию.
- Операция дифференцирования сопоставляет заданной
функции F (x ) ее производную.
F![]() (x)
= f
(x).
(x)
= f
(x).
Учитель : В чем заключается задача , дифференцированию?
Вывод учащихся :
- Исходя из данной функции f (x) , найти такую функцию
F (x) производной которой является f (x) , т.е.
f
(x)
= F![]() (x)
.
(x)
.
Учитель :
Такая операция называется интегрированием, точнее
неопределенным интегрированием.
Раздел математики, в котором изучаются свойства операции интегрирования функций и ее приложения к решению задач физики и геометрии, называют интегральным исчислением.
Интегральное исчисление _ это раздел математического анализа, вместе с дифференциальным исчислением, оно составляет основу аппарата математического анализа.
Интегральное исчисление возникло из рассмотрения большого числа задач естествознания и математики. Важнейшие из них - физическая задача определения пройденного за данное время пути по известной, но быть может переменной скорости движения, и значительно более древняя задача – вычисления площадей и объемов геометрических фигур.
В чем состоит неопределенность этой обратной операции предстоит выяснить.
Введем определение. ( кратко символически записывается
на доске ).
Определение 1. Функцию F (x) , заданную на некотором промежут
ке X, называют первообразной для функции задан-
ной
на том же промежутке, если для всех x
![]() X
X
выполняется равенство
F![]() (x)
= f
(x)
или d
F(x)
= f
(x)
dx
.
(x)
= f
(x)
или d
F(x)
= f
(x)
dx
.
Например. ( x![]() )
)![]() = 2x, из
этого равенства следует, что функция
= 2x, из
этого равенства следует, что функция
x![]() является первообразной на всей числовой
оси
является первообразной на всей числовой
оси
для функции 2x.
Используя определение первообразной , выполните упражнение
№ 2 ( 1,3,6 ) . Проверьте, что функция F является первообраз-
ной для функции f, если
1) F
(x)
=
![]() 2 cos
2x
, f
(x)
= x
2 cos
2x
, f
(x)
= x![]() - 4 sin
2x
.
- 4 sin
2x
.
2) F (x) =
tg![]() х
- cos 5x , f (x) =
х
- cos 5x , f (x) =
![]() + 5 sin 5x.
+ 5 sin 5x.
3) F (x)
= x![]() sin x +
sin x +
![]() , f (x) = 4x
, f (x) = 4x![]() sinx + x
sinx + x![]() cosx +
cosx +
![]() .
.
Решения примеров записывают на доске учащиеся, комменти-
руя свои действия.
Учитель :
Является
ли функция х![]() единственной первообразной
единственной первообразной
для функции 2х ?
Учащиеся приводят примеры
х![]() + 3 ; х
+ 3 ; х![]() - 92, и т.д. ,
- 92, и т.д. ,
Вывод делают сами учащиеся :
любая функция имеет бесконечно много первообразных.
Всякая
функция вида х![]() + С, где С – некоторое число,
+ С, где С – некоторое число,
является
первообразной функции х![]() .
.
Теорема о первообразной записывается в тетради под диктовку
учителя.
Теорема. Если функция f имеет на промежутке первообраз-
ную F, то для любого числа С функция F + C также
является первообразной для f . Иных первообразных
функция f на Х не имеет.
Доказательство проводят учащиеся под руководством учителя.
а) Т.к. F - первообразная для f на промежутке Х, то
F![]() (x) = f (x) для всех х
(x) = f (x) для всех х
![]() Х.
Х.
Тогда
для х![]() Х для любого С имеем :
Х для любого С имеем :
( F
(x)
+ C
)![]() = f
(x)
. Это значит, что F
(x)
+ C
- тоже
= f
(x)
. Это значит, что F
(x)
+ C
- тоже
первообразная f на Х .
б) Докажем , что иных первообразных на Х функция f
не имеет.
Предположим , что Ф тоже первообразная для f на Х.
Тогда
Ф![]() (x)
= f
(x)
и потому для всех х
(x)
= f
(x)
и потому для всех х
![]() Х
имеем :
Х
имеем :
Ф![]() (x)
- F
(x)
- F![]() (x)
= f
(x)
- f
(x)
= 0, следовательно
(x)
= f
(x)
- f
(x)
= 0, следовательно
Ф - F постоянна на Х. Пусть Ф (x) – F (x) = C , тогда
Ф (x) = F (x) + C, значит любая первообразная
функции f на Х имеет вид F + C.
Учитель : в чем заключается задача отыскания всех первообраз-
ных для данной функции ?
Вывод формулируют учащиеся:
Задача отыскания всех первообразных, решается
отысканием какой-нибудь одной: если такая первооб-
разная найдена, то любая другая получается из нее
прибавлением постоянной.
Учитель формулирует определение неопределенного интеграла.
Определение 2. Совокупность всех первообразных функции f
называют неопределенным интегралом этой
функции.
Обозначение.
![]() ;
;
![]() - читается интеграл.
- читается интеграл.
![]() = F
(x)
+ C,
где F
– одна из первообразных
= F
(x)
+ C,
где F
– одна из первообразных
для f , С пробегает множество
действительных чисел.
f - подынтегральная функция;
f (x)dx - подынтегральное выражение;
х - переменная интегрирования;
С - постоянная интегрирования.
Свойства неопределенного интеграла учащиеся изучают по учебнику самостоятельно и выписывают их в тетрадь.
-
d (
 ) = f (x) dx.
) = f (x) dx. -
 = F (x)
+ C.
= F (x)
+ C. -
Интеграл суммы равен сумме интегралов слагаемых.
![]() =
=
![]() +
+
![]() .
.
-
Постоянный множитель можно вынести за знак интеграла.
![]() = A
= A![]() .
.
-
T.k. ( x
 )
) = (
= (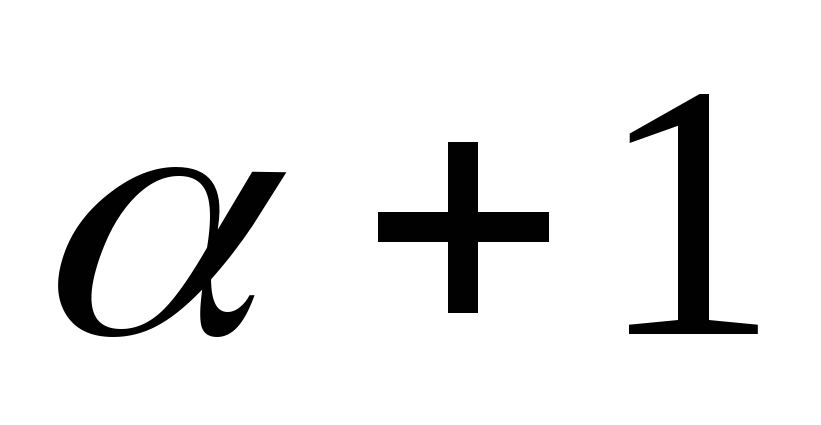 ) x
) x ,
то при
,
то при
 - 1,
- 1,
![]() =
=
![]()
![]() =
=
![]() + С.
+ С.
Применение сделанных выводов на практике, в процессе решения примеров.
Используя свойства неопределенного интеграла, решите примеры № 1 (2,3 ).
Вычислите интегралы.
-
 ,
, -
Какие свойства неопределенного интеграла следует применить, решая следующий пример ?
![]() .
.
Решения учащиеся записывают в тетрадях, работающий у доски
комментирует выполняемые действия.
Учитель :
Теперь вы можете решить физическую задачу
определения пройденного пути по известной скорости ?
по известному ускорению ?
Решите задачи № 3 и 4 и запишите решение в тетрадь.
Учитель выборочно проверяет запись решения.
Решите задачу. Тело свободно падает в пустоте. Пусть s (t) –
координата тела в момент t .
Т.о.
g
= s![]() (t)
и g
- постоянная.
(t)
и g
- постоянная.
Требуется найти функцию s (t) – закон движения.
