Алгоритм

Шаг 1. Задать исходные данные: начальный интервал неопределенности L₀ [a₀ , b₀ ], точность l >0.

Шаг 2. Положить k =0.

Шаг 3. Вычислить

y₀ a₀ ³ ₂ ⁵ (b₀ a₀ ); z₀ a₀ b₀ y₀ .

Шаг 4. Вычислить f ( y_k ) , f ( z_k ) .

Шаг 5. Сравнить f ( y_k ) с f ( z_k ) :

а) если f ( y_k ) f (z_k ) , то положить a_{k 1} a_k , b_{k 1} z_k и y_{k 1} a_{k 1} b_{k 1} y_k , z_{k 1} y_k . Перейти к шагу 6;

б) если f ( y_k ) f (z_k ) , положить a_{k 1} y_k , b_{k 1} b_k и ^yk 1 ^zk ^{, z}k 1 ^ak 1 ^bk 1 ^zk ^.

Шаг 6. Вычислить L_k | b_{k 1} a_{k 1} | и проверить условие окончания:

10

а) если L_k l , процесс поиска завершается и в качестве приближенного решения можно взять середину последнего интервала:

_x* ^ak 1 ^bk 1 _;

2

б) если L_k l , положить k k 1 и перейти к шагу 4.

1.1.5. Метод Пауэлла

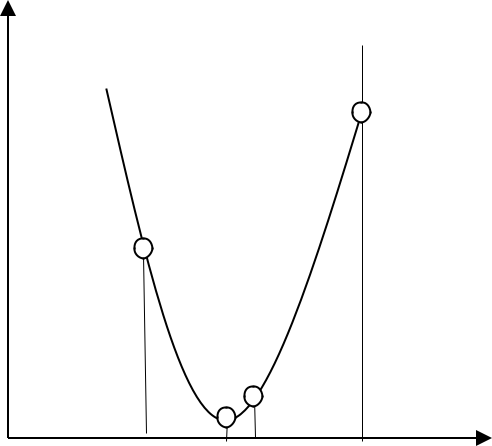
Суть метода: определить три точки в направлении уменьшения функции и рассчитать квадратичную аппроксимацию. Сравнить значение функции в наилучшей из трех точек и в точке квадратичной аппроксимации и если условие останова не выполняется, то выбирается наилучшая точка и две точки по обе стороны от неё. Так на рис. 1.5 будет выбрана точка x и две точки по обе стороны ( x₁ , x₂ ) .

y

x1 ˉx x2 x₃ x

Рис.1.5 Определение точек методом Пауэлла

Алгоритм

Исходные данные: x₁ - начальная точка; x - выбранная величина шага по оси x .

Шаг 1: Вычислить x₂ x₁ x .

Шаг 2: Вычислить f (x₁) и f ( x₂ ) .

11

Шаг 3: Если f (x₁) f (x₂ ) , положить x₃ x₁ 2 x , если f (x₁) f (x₂ ) , то x₃ x₁ x . Если x₃ x₁, то перенумеровать точки в естественном порядке: x₁ x₃ , x₂ x₁ , x₃ x₂ .

Шаг 4: Вычислить f ( x₃ ) и найти

F_min min{ f₁, f₂ , f₃} .

24. _min равно точке x_i , которая соответствует F_min .

Шаг 5: По трем точкам

x1, x2 , x3

вычислить

x ,

используя квадратичную

аппроксимацию

af (x2 ) f (x1 ) ,

1

x2 x1

1

f (x3 ) f (x1 )

f (x2 ) f (x1 )

a2

,

xx

xx

x

2

x

3

2

3

1

1

x2 x1

a1

.

x

2

2a2

Шаг 6: Проверка на окончание поиска:

Fmin f (

)

;

а) является ли разность

x

X min

,

б) является ли разность

x

где 0 и 0 - заданные точности.

Если условия а) и б) выполняются одновременно, то закончить поиск (в качестве результата взять точку x ). Иначе переход на Шаг 7.

Шаг 7: Выбрать "наилучшую" точку ( X _min или x ) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти на Шаг 4.

Замечание: после пятого шага необходимо провести дополнительную проверку, т.к. точка x может находиться за интервалом ( x₁ , x₃ ). В этом случае точка x₁ заменяется x и осуществляется переход к шагу 1.

12

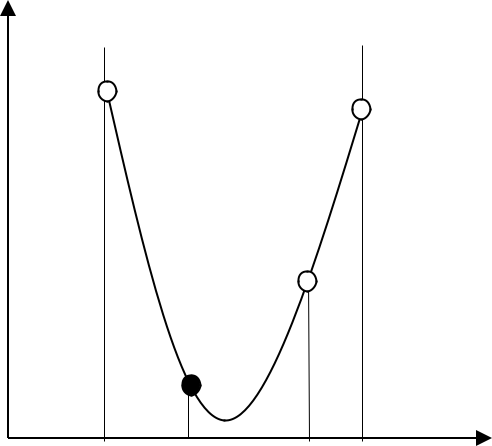
1.1.6. Метод Монте-Карло

Суть метода: на интервале [ a ₀ , b₀ ] случайным образом генерируются точки, в каждой точке вычисляется значение функции. Выбирается точка, в которой значение функции минимально (рис.1.6).

y

a₀ x1 x2 b₀ x

Рис.1.6 Метод Монте-Карло (точки x₁ и x₂ сгенерированы случайным образом)