Интегрирование тригонометрических выражений
.docИнтегрирование тригонометрических выражений
1. Интегралы
вида
.
Эти интегралы с помощью известных тригонометрических формул:
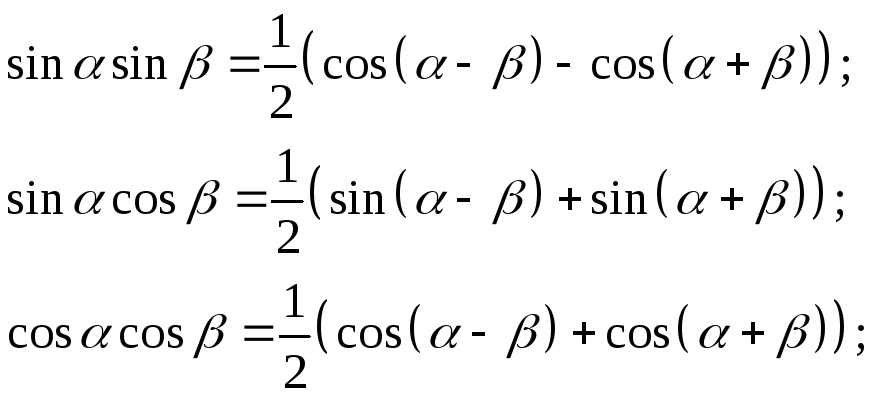
приводятся к интегралам
Пример.
Найти
Так
как
,
то
2. Интегралы
вида
,
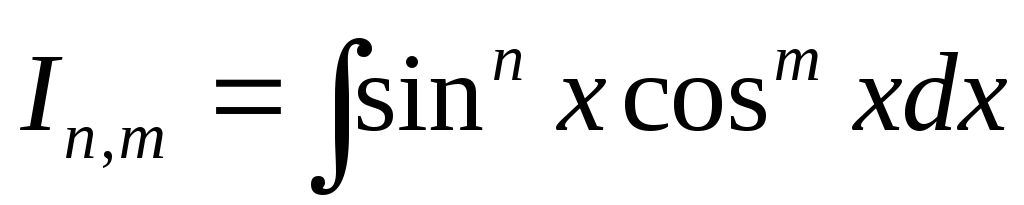где
n
и
m
- натуральные
числа.
Если
п и
т четные,
то интегралы
находятся с помощью
тригонометрических
формул
Если хотя бы одно из чисел пит нечетное, то от нечетной степени отделяется множитель первой степени и вводится новая переменная.
Пример.
Найдите
.
Имеем
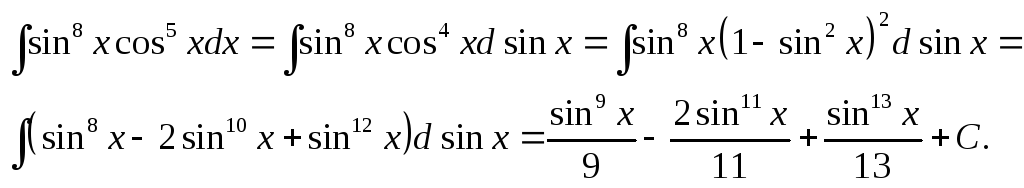
3. Интегралы
вида
,
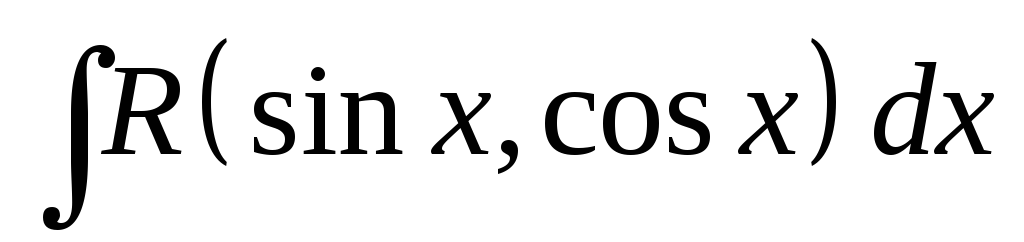где
R(u,
v)
- рациональная
функция двух аргументов u
и v.
Покажем,
что интеграл
может
быть сведен к
интегралу от рациональной функции
аргумента
Действительно,
Из
подстановки
следует, что
Таким образом
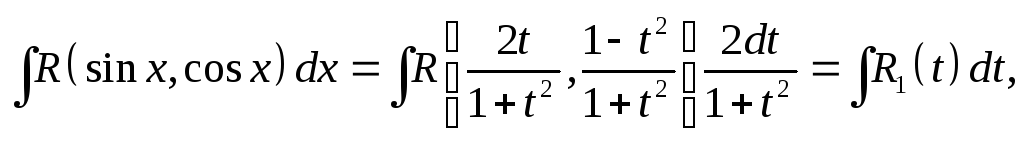где
-
рациональная функция.
Пример.
4. Интеграл
вида
.
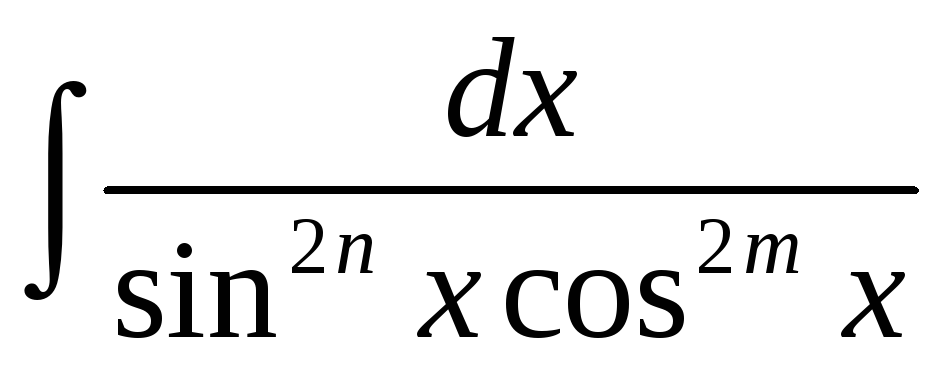Может
быть сведен к интегралу от рациональной
функции аргумента
(или
).
Заметим, что
или 
.
Оставшаяся
вне дифференциала дробь выражается
через
с помощью формул
или 
.
Пример.
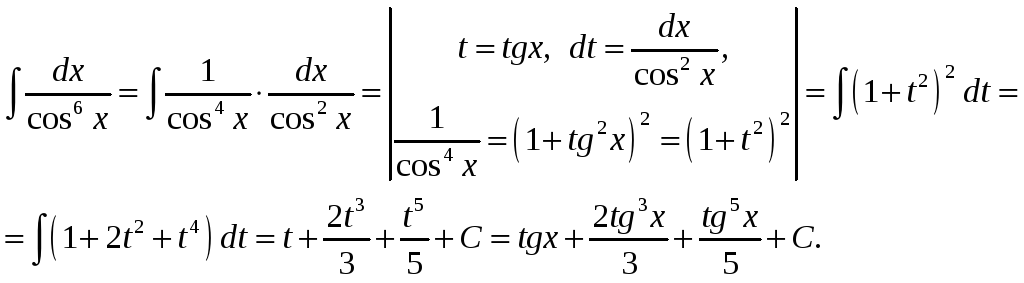
5. Интегралы
вида
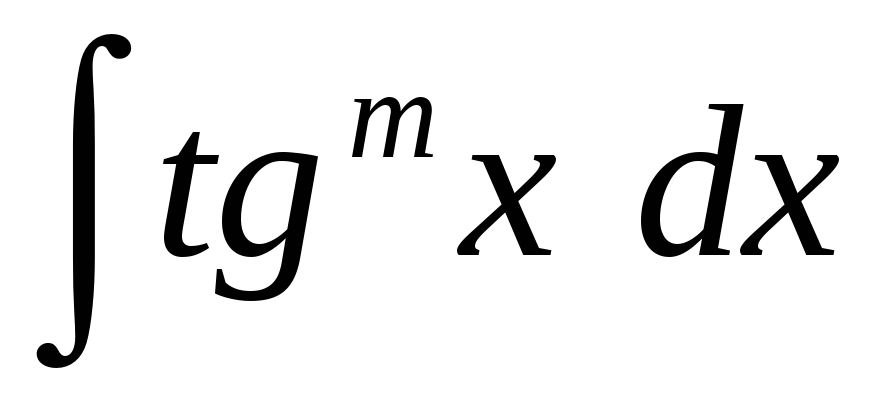или
.
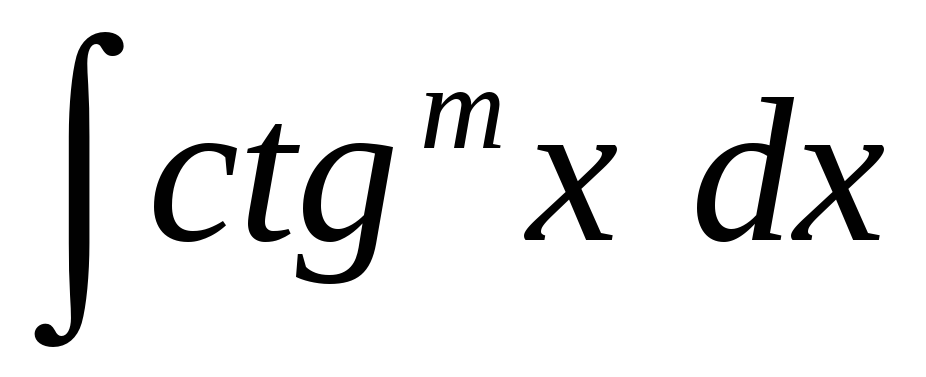Отделяется
множитель
(или
)
и представляется как
(или
).
Получается разность двух интегралов,
один из которых берется заменой
(или
),
а во втором, при необходимости, снова
отделяют
(или
).
Пример.
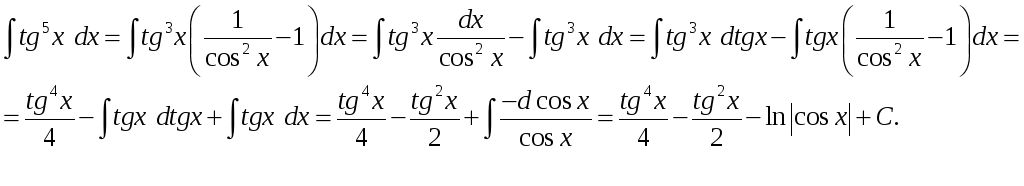
6. Особые приемы.
К числу особых приемов, применяющихся при интегрировании тригонометрических выражений, может быть отнесено представление «тригонометрической единицы».
Пример.
-
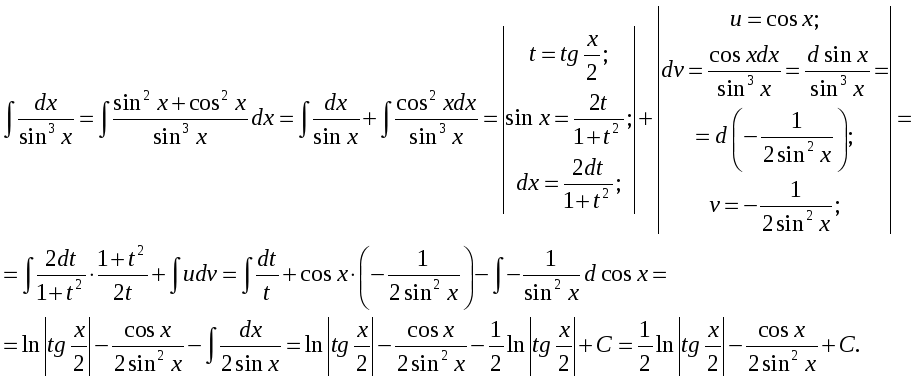
Задания для самостоятельного выполнения.
1)
2)
3)
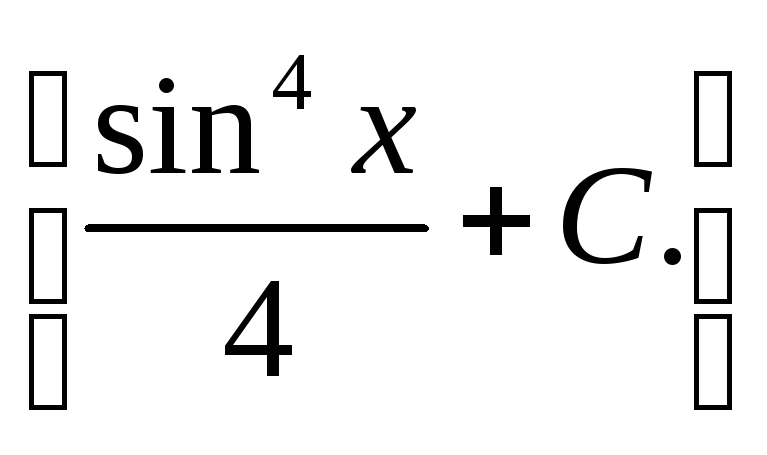
4)
5)
6)
7)
8)
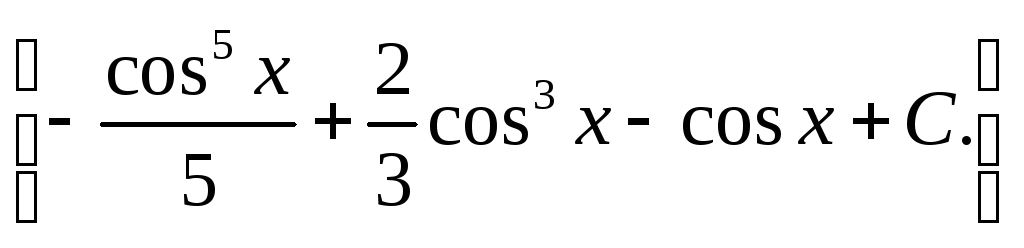
9)
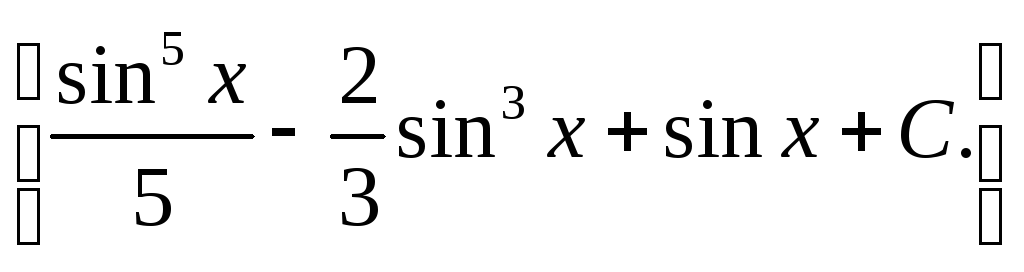
10)
12)
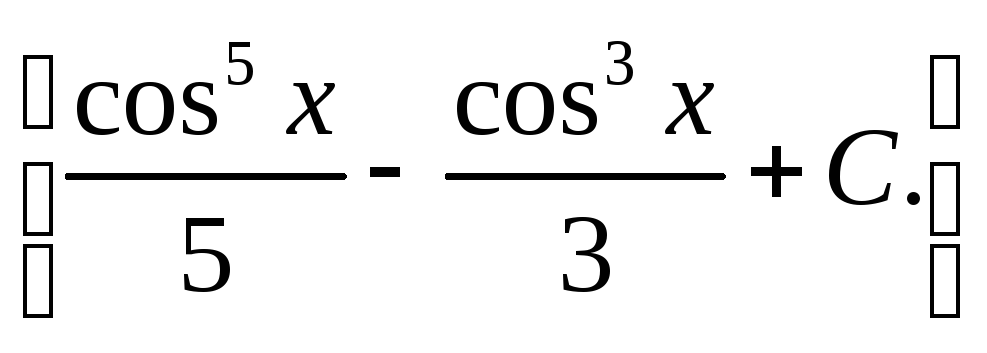
13)
