reading / British practice / Vol D - 1990 (ocr) ELECTRICAL SYSTEM & EQUIPMENT

pruy- Fc TIRE SHEATH

TEMPERATURE SENSITIVE DIELECTRIC MATERIAL

with a continuous conductor temperature of 90 ° C and a short-circuit temperature of 250 ° C, smaller conductor sizes can therefore be used than would be required if PVC insulation were used for the same duty.

For multicore control cables, PVC primary insulation is generally being replaced by a dual layer of EP R/ EVA. The layer of EPR provides the required electrical performance whilst the outer layer of EVA gives sufficient fire performance to pass the test on a single insulated wire, which is detailed in Section 8 of this chapter.

For multipair control cables, the PVC insulation is being replaced by high performance thin-wall insulations such as polyphenol oxide (NORYL — a General Electric (USA) trade name) and poly ether ether ketone (PEEK — an Imperial Chemical Industries trade name). Both these materials are thermoplastic but in the case of PEEK, cables insulated with this material are capable of operating at temperatures in excess of 250 ° C under defined conditions. However, at the time of writing, these materials are considerably more expensive than PVC.

One of the difficulties with these developments is that the material formulations are new and there is little service experience with them compared to PVC which has been used for over thirty years. Therefore it is essential that cables employing such new materials are adequately evaluated before putting them into service; the remaining parts of this section define tests that are used for this purpose.

CROSS SECTION OF

DETECTOR CABLE PROTECTIVE

SHEATH

FIG. 6.11 Analogue-type linear heat detecting cable

propagation performance and reduced gas emissions are given in Section 8 of this chapter.

The basic construction of cables has remained the same but new compounds have been substituted for PVC. For cable beddings and sheaths, currently the inost commonly used replacement for PVC is ethy- lene vinyl acetate copolymer (EVA). EVA is available in both thermoplastic and thermosetting forms. For thermosets, curing can be achieved by continuous vulcanisation by steam or pressurised liquid, and also by immersion in hot water if the silane compound method has been used. These materials are filled with

alurninituirt hydroxide to give reduced fire propagation performance

Whereas PVC has been used in the past for primary insulation on power cables, this is generally being

changed to ethylene propylene rubber (EPR) or cross- linked polythene (XLPE) which has hitherto only been used on single -core power cables. Thermosetting EVA is also being used in some cases for power cable in- sulation. All insulation materials are suitable for use

For normal service life, one of the significant degradation processes in cables is the ageing of their non-metallic materials. It is therefore important to evaluate cables to ensure that they can operate at the required temperature for their service life. For many non-metallic materials the degradation process can be defined by a single temperature-dependent reaction that follows the Arrhenius equation:

where K = reaction rate

A = frequency factor

= 2.718

E a = energy needed to activate the degradation reaction (electron volts)

kB = Boltzmann's constant (8.617 x 10 -5 eV/K)

T = absolute temperature, K

This can be transferred into a form which yields an acceleration factor, defined as the service life divided by ageing time, as follows:

To apply this formul a, the service temperature and required life of the cable must be defined together with the activation energies of the materials involved. As far as service temperature is concerned, this should be the estimated average service temperature over the life of the cables. For example, cables are generally sized against maximum ambient conditions which allow for peak summer temperatures and the least effective air conditioning. In reality this means that a cable capable of working at a maximum continuous operating temperature of, say, 90 ° C may in fact be operating at an average annual temperature in the order of 75 ° C. Typical mean service temperature conditions are:

It is normal practice to take the service time as the design life of the power station. This may vary from 25 years to 40 years, or 50 years for hydro stations. It is considered good practice to ignore reduction in service life due to maintenance outages or two - shifting during the later years of conventional plant, as this allows some margin in the predicted life of the cables.

Having defined the service conditions it is now necessary to establish the activation energy of all essential non - metallic materials within the cable. The term essential is used since, for example, some binder tapes are included in cables purely for manufacturing purposes and therefore if they failed mechanically they would not affect service life.

The activation energy of non-metallic materials may be determined by carrying out ageing tests on samples at a number of temperatures. A typical criterion for ageing performance evaluation is to assess the time it takes for the material's 'elongation at break' to reduce to occur at 1.5 times its initial length (50 070 absolute). Dumb-bell samples, of the type shown in Fig 6.12, are therefore used and these are aged in circulating air ovens. Samples are aged at a number of temperatures (say four), these being at least 10 ° C apart and with a maximum temperature of (typically)

3mm

50,11

FIG. 6.12 Details of dumb-bell samples

160° C to ensure the degradation mechanism is still representative of that occurring at the service temperature. For some high temperature materials it necessary to exceed 160 ° C to give acceptable testing ti mes, but even then a typical test programme can last up to 2 years. Samples of materials are removed from the ovens until the time is determined at which the material exhibits 50 070 absolute elongation at break. A typical graph of such results is shown in Fig 6.13. From the four test results, a graph of reciprocal temperature against logarithm of time is plotted as shown in Fig 6.14. The Arrhenius activation energy is determined from the slope E a /kB of this graph using the method of least squares. For polymeric cable materials the activation energies are normally in the range of 0.85 and 1.65 eV.

Having established the cable service conditions and material activation energies formula, Equation 6.2) can be used to calculate accelerated ageing time : for test purposes. Typical ageing times for various -:m- peratures and activation energies are shown in Tables 6.3 and 6.4.

From this information, the ageing time and temperature appropriate to the essential cable material having the lowest activation energy can be selected. Actual cable samples are then subjected to this ageing regime after which they are subjected to electrical and mechanical tests to ensure they are still serviceable.

3.11 Mechanical performance

The mechanical properties of cables must be such that they will withstand the rigours of being installed along routes which could consist of horizontal and vertical ladder racks, through ducts and conduits, or direct in the ground. After installation cables must withstand the environmental conditions into which they are placed and these could include damp or oil contaminated situations.

Materials such as PVC and PE have been freely available since the 1950s and therefore the mechanical performance of cables constructed from such materials has been evaluated and proved satisfactory from long

TABLE 6.3

Power cable (service life 40 years at 75° C) ageing times at various temperatures

experience. When introducing new cables into cable construction it is important to evaluate their mechanical properties and the performance of PVC can form a useful benchmark for such tests. Quite clearly the performance of the oversheath is of major importance and therefore the majority of testing must be concerned with evaluating this item.

A typical range of type tests to evaluate mechanical performance includes:

• Abrasion on complete cable.

TABLE 6.4

Control cable (service life 40 years at 40° C) ageing times at various temperatures

•Sheath cut-through.

•Crush on complete cable.

•Ozone resistance of insulation and oversheath.

•Water permeation on bedding and oversheath materials.

•Long term water immersion test.

•Mineral oil resistance of oversheath.

•Pulling lubricant resistance of oversheath.

•Tear resistance of oversheath.

•Retraction of oversheath.

•Hot set on insulation, bedding and oversheath if cross-linked.

I o'

1 03

1 02

z1 0) VT

FIG. 6.14 Arrhenius plot

•Tensile strength and elongation at break on insulation, bedding and oversheath.

•Sheath penetration.

•Hot pressure and hot deformation.

Cut-through, crush, water permeation and tensile strength tests should be carried out on both aged and non-aged samples, the remaining tests being carried out on nonaged samples only.

Many of these tests are covered by British or International Standards such as BS2782, BS6469, IEC 229 and IEC 540, and therefore further details are not included in this volume. However, the cut-through, crush, water immersion, oversheath retraction and penetration tests are less common and further details of these are included.

The cut-through test is designed to measure the capability of the oversheath to withstand being rested on a sharp edge such as that which might occur with a cable tray. This test is performed using a tensile

test machine operating in its compressive mode t, drive a cutting edge (see Fig 6.15) through the Over sheath of a complete cable sample. The force required to achieve this is monitored and compared against the acceptance criteria. The test is carried out at both ambient temperature and the estimated sheath operating temperature. The crush test is similar to the cut. through test, but the cutting edge is replaced by two parallel flat steel blocks 50 mm wide. In this case all metallic components in the cable are monitored and the force required to produce an electrical short is recorded and compared with the acceptance criterion. This test is intended to simulate a cable being crushed by, say, being walked on. The sheath penetration test is designed to simulate a cable being pulled over a sharp edge such as a hexagonal bolt head. In this test a weighted spike is moved along the cable sheath as shown diagrammatically in Fig 6.16. The acceptance

Am, Mint BEFORE

START OF RADIUS

CABLE UNDER TEST

FIG. 6.15 Cut-through test

FIG. 6.16 Sheath penetration test

Section 4.2 deals w ith the current rating of cables for continuous operation which, for single-core cables, includes the sheath armour voltage with single point bonding and current sharing with more than one cable per phase.

Section 4.3 covers the three types of abnormal condition. These are short-circuit fault, earth fault and overload current, and considers their magnitude and duration relative to cable size for the prevention of thermal damage.

Section 4.4 is a review of motor starting requirements and the determination of motor starting currents and times for different motor sizes.

Section 4.5 deals with the calculation of voltage regulation, i.e., the percentage voltage drop in a supply system due to the impedance of the cables under both steady state and motor starting conditions. The appropriate cable sizes are determined for the voltage regulation limits within which the electrical plant and equipment is specified to operate.

Section 4.6 examines the overall process of power cable system design as applied to feeder and motor circuits. This describes how the various technical requirements are applied at each system voltage level and includes additional requirements specific to certain types of 415 V circuit.

In the final part, the step-by-step procedure followed in selecting a cable size is demonstrated in a number of worked examples.

In practice, the determination of each cable size by calculation is a repetitive and time consuming process. Consequently, tables have been developed for this purpose which enable the correct size to be quickly determined. In the case of continuous current ratings, these allow adjustments to be made for variations in the installation conditions. Some tables, but not all as they are too numerous, are included in the appendices to this chapter.

It is necessary to have available certain design information before the task of power cable system design can commence. This, in turn, calls for the design of the power station electrical auxiliary system and plant layout/nfajor cable routes to be reasonably well advanced. To gain an initial appreciation of what this means, the extent of the design information needed is as follows:

•Types of fault current breaking device and current rating.

•Design load currents for feeder circuits.

•Motor sizes and starting time for large motors.

•Fault levels.

•Protection relay operating times.

•Voltage regulation limits.

•Cable route lengths.

•Types and details of cable routes.

•Ambient temperatures for cables laid in air.

•Soil conditions for buried cables.

•Installation configurations for single-core cables with more than one cable per phase.

In practice, difficulty is usually experienced in obtaining all of this information when cable sizing has to start and therefore assumptions may have to be made in order that the task can proceed.

4.2 Current rating for continuous operation

The maximum or permissible current for continuous (or sustained) AC operation is determined, for a given cable conductor size, by the design of the cable and the conditions under which it is installed.

The principal factors concerned may be summarised

as:

Design of cable

•Conductor material.

•Maximum conductor temperature for insulation.

•Operating voltage.

•Number of load-carrying conductors.

•Cable overall construction. ,

Conditions under which installed

•Ambient temperature.

•Type of cable route.

•Method of installation.

•Method of armour bonding.

The way each of these factors is taken into account can best be described by showing how the permissible current rating of a cable is calculated for the three types of cable route normally employed, i.e., cables laid in air, buried direct in the ground or laid in ducts. As will be seen, this process is solely concerned with ensuring that the temperature of the insulation does not exceed a maximum limit. Each of the above factors is involved with either the determination of the total heat produced within the cable, or affects the way this heat is lost to the surroundings. The current which balances these two during continuous operation at the maximum temperature limit is the permissible current

rating of the cable. The following describes in more detail how this current rating is derived.

Maximum conductor temperature

4.2.1

heat is produced in a cable as the result of electrical lo“es due to the flow of current in the metallic components, i.e., conductors, screens and armours, and the presence of voltage. i.e., dielectric losses in the insuIdtion. The hottest part of the cable is the conductor and heat flows outwards to the cable surface to be Liissipated to the surrounding medium by conduction,

nvection and radiation as shown in Fig 6.17,

co If the cable current is steady, the cable temperature riNes above ambient until thermal equilibrium is reached ,,dien the rate at which heat is produced is equal to the rate at which it is lost to the surroundings, as hown for the conductor temperature in Fig 6.18,

Power cable system design

The time taken to reach peak temperature is much shorter for cables laid in air than buried direct in the ground. Typically, for a large size cable, this is 2 - 4 hours when laid in air and in excess of 24 hours when buried direct in the ground.

In Fig 6.18, the equilibrium temperature is just below the cable upper temperature limit, termed the maximum conductor temperature, for continuous operation. The value of this limit is normally determined by the choice of insulation and is derived from consideration of the electrical and mechanical properties of the insulation at the maximum conductor temperature. In particular, these properties must be retained without significant deterioration for a reasonable service life. Softening, leading to thinning of the insulation, during a thermal overload can also be a limiting factor with thermoplastic materials. By international agreement, standard maximum conductor temperatures have

RADIAL HEAT FLOW IS REASONABLY UNIFORM WITHIN THE CABLE BUT is NOT SO EXTERNALLY

CONDUCTOR

INSULATION

BEDDING

/1 ARMOUR

TEMP

AMBIENT TEMP

DISTANCE FROM CABLE CENTRE

FIG. 6.17 Heat flow in cable

MAX CONDUCTOR TEMP

PEAK TEMPERATURE

CONDUCTOR TEMP RISE

been assigned to all commonly-used insulation types and grades. Examples of these are shown in Table 6.5.

TABLE 6.5

Maximum conductor temperature

CABLE ENERGISED

TIME

4.2.2 Ambient temperature

The conductor equilibrium temperature is equal to the sum of the ambient temperature plus the temperature rise. It therefore follows that before the temperature rise (i.e., current rating) can be determined, the ambient temperature must be known.

The ambient temperature depends on the cable en- vironment, which for cables laid in air is the surrounding air temperature and for cables buried direct in the ground is the soil temperature. Outdoors, the air temperature varies with geographical location, season, ti me of day, etc., which in turn influences the soil temperature. Inside a power station, the air temperature is closely controlled in certain rooms, but elsewhere varies with location from being approximately external air temperature in unheated areas to 50 ° C in parts of a boiler house or nuclear reactor building.

In deciding the value to be adopted, it is not the mean but the highest ambient temperatures that need to be considered if the maximum conductor temperature is not to be exceeded. On this basis, values are selected for each cable environment. For outdoor environments, recommended temperatures are available and these are normally utilised. Typical values for cable ambient temperatures are shown in Table 6.6.

TABLE 6.6

Cable ambient temperatures

If for a cable laid in air the ambient temperature varies over different portions of the cable route, then clearly the highest ambient temperature involved must be used for cable sizing. With the large number of cables required for a power station, many of which will have parts of their route length at different ambient temperatures, the process of determining the correct ambient temperature for each cable becomes impractical. Therefore a high ambient temperature is adopted which covers all the cables within the power station, except for a few cables in extreme ambient temperature areas such as close to a boiler. These latter cables are easily dealt with separately.

4.2.3 Conductor temperature rise

The steady state conductor temperature rise may be calculated mathematically, enabling the permissible current rating to be determined for a known ambient

and maximum conductor temperature. Account is taken of the heat input from each electrical loss, relative to its position within the cable, and the heat flow through each non-metallic component to the surrounding medium. This treatment is described in IEC287 [II and for AC operation is obtained from the following formula:

= current flowing in one conductor, A

R = alternating current resistance per unit length of the conductor at maximum operating temperature, f2/m

Wd = dielectric loss per unit length for the insulation surrounding the conductor, W/m

T2 = thermal resistance per unit length of the bedding between sheath and armour, K.m/W

13thermal resistance per unit length of the external serving of the cable, K.m/W

14= thermal resistance per unit length between the cable surface and the surrounding medium, K.m/W

=number of load-carrying conductors in the cable (conductors of equal size and carrying the same load)

X = ratio of losses in the metal sheath to total losses in all conductors in that cable

X2 = ratio of losses in the armouring to total losses in all conductors in that cable

Note: The expression is written in general terms. When applied to polymeric insulated cables, sheath becomes metallic screen (for 11 kV cables in power stations) and external serving becomes oversheath.

The current rating for a four-core low voltage cable may be taken to be equal to the current rating of a three-core cable for the same voltage rating, conductor size and construction when used in a three-phase system with the fourth conductor as neutral.

The dielectric losses (Wd) may be neglected for cables where the voltage between conductors and earth is less than 15 kV for EPR, 37 kV for XLPE and 6 kV for PVC, which is the case for the cables used

Metallic screen and armour loss ratios (X and X2)

Cable metallic screen and armour losses are produced by circulating currents and to a much less extent eddy

dc = diameter of conductor, mm

t = thickness of insulation between conductor and metallic screen, mm

Semi-conducting layers are considered part of the insulation. The thermal resistance (T2) between metallic screen and armour is given by:

t2 = thickness of bedding, mm

D s = external diameter of metallic screen, mm

The thermal resistance (13) of the oversheath is given

1

T4 —

Deh(&00 7

( D e )g

where D e = external diameter of cable, m

h = heat dissipation coefficient, W/m2 (K)E 25

AOs = excess of cable surface temperature above ambient temperature, K

The heat dissipation factor constants Z, E and g for one, two or three cables either installed spaced or touching, supported away from or cleated direct to a vertical wall, are detailed in IEC 287.

Cables installed outdoors in air are normally shielded from the sun, but if directly exposed, separate calculations must be performed which take account of the heating due to solar radiation.

Cables buried direct in the ground The thermal resistance for a single isolated buried cable is given by:

where QT = the thermal resistivity of the soil, K.m/W

= 2L/D,

L = distance from the surface of the ground to the cable axis, mm

To calculate the thermal resistance of the insulation for multicore cables reference should be made to IEC

287.

External thermal resistance (Ed

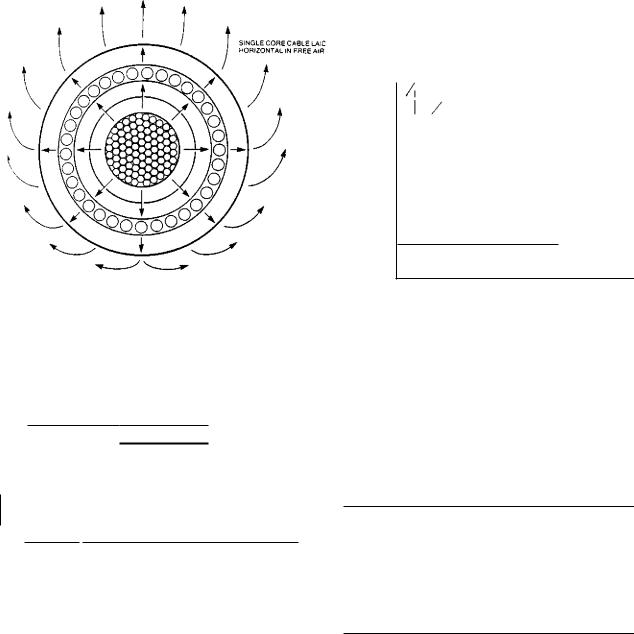
Cables laid in free air (protected from solar radiation) Heat dissipation from an isolated cable laid in free air is mainly by convection, but a proportion will be emitted by radiation to be absorbed by the enveloping surface or transmitted by conduction to the cable support system. In this respect, cables with larger diameters dissipate heat better than smaller cables because of the increased surface area. The close proximity of other cables or a vertical wall reduces heat dissipation. For example, with three single-core cables the heat dissipation and hence current rating is lowest when they are installed in trefoil. The heat dissipation and current rating is improved when the cables are placed in a flat spaced vertical formation and the highest rating is achieved with a flat spaced horizontal formation.

D e = external diameter of cable, mm

The thermal resistivity of the soil depends on the backfill material, degree of compaction, make-up of the original ground and moisture content. Thorough compaction of the backfill material is essential to obtain a satisfactory resistivity. Of the remaining factors, the most important is moisture content which varies the soil thermal resistivity to such an extent that, for most purposes, the effect of soil type can be ignored. This variation is shown in Table 6.8.

At depths of 0.8 m and less, the soil moisture content is dependent on the prevailing weather which varies with geographical location, time of year, etc. Soil thermal resistivity is difficult to measure and for most applications it is convenient to use a standard value representative of the all year round maximum soil thermal resistivity. This condition in average soil (i.e., clay or loam) is when the soil is damp but not quite moist, corresponding to a value of 1.2 K.m/W.