2 семестр / Лекции по ВМ2

вательность. Пусть подпоследовательность {Mkn } → A. В силу леммы 3 точка A {M} и поэтому функция f(M) непрерывна в точке A. Следовательно, {f(Mkn )} → f(A), а это противоречит тому, что {f(Mkn )} — бесконечно большая последовательность. Полученное противоречие доказывает, что наше предположение не верно и, следовательно, функция u = f(M) ограничена на множестве {M}.

Замечание. Если множестве {M} не является ограниченным или не является замкнутым, то непрерывная на таком множестве функция u = f(M) может быть неограниченной на этом множестве.

Задание. Придумайте соответствующие примеры.

Определение. Число U называется точной верхней гранью

функции u = f(M) на множестве {M}, если

Аналогично определяется точная нижняя грань функции:

inf f(M).

{M}

Теорема 12 (вторая теорема Вейерштрасса). Непрерывная на замкнутом ограниченном множестве функция достигает на этом множестве своих точных нижней и верхней граней.

Теорема доказывается так же, как и аналогичная теорема для

функции одной переменной.

Определение. Функция u = f(M) называется равномерно непрерывной на множестве {M}, если ε > 0 δ > 0 (зависящее только от ε), такое, что M1 и M2 из множества {M}, удовлетворяющих условию ρ (M1, M2) < δ, выполняется неравенство

|f(M1) − f(M2)| < ε.

Задание. Придумайте пример функции двух переменных u = f(x, y), которая является: а) равномерно непрерывной на некотором множестве; б) непрерывной, но не равномерно непре-

рывной на некотором множестве.

Теорема 13 (Кантора). Непрерывная на замкнутом ограниченном множестве функция равномерно непрерывна на этом множестве.

Теорема доказывается так же, как и для функции одной переменной.

u(x, y) не является непрерывной в точке O(0, 0). Таким образом, это пример функции, разрывной в точке, но тем не менее имеющей в этой точке частные производные. Для функций одной переменной такая ситуация невозможна.

Рис. 9.6. Рис. 9.7.

Физический смысл частной производной. Частная производная ∂u∂x(M) характеризует скорость изменения функции в

точке M в направлении оси Ox.

Замечание. Если M — граничная точка области определения функции, то для нее введенное определение частной производной может быть непригодно. Например, для точки M0 на рис. 9.7 не существует частное приращение xu. В этом случае, если

= f(x1, ... , xm) во внутренней точке M(x1, ... , xm) из области определения функции:

u = f(x1 + x1, ... , xm + xm) − f(x1, ... , xm).

Определение. Функция f(x1, ... , xm) называется дифференцируемой в точке M(x1, ... , xm), если ее полное приращение в этой точке можно представить в виде

Равенство (9.5) назовем условием дифференцируемости

функции в точке M(x1, ... , xm).

Физический смысл дифференцируемости функции многих переменных

Поставим такой вопрос: можно ли скорость изменения функции u(x, y) по любому направлению в точке M выразить через

скорости ∂u∂x (M) и ∂u∂y (M)? Оказывается, что не всегда. Если

u(x, y) дифференцируема в точке M, то можно. Это станет ясно из дальнейшего.

Вспомним, что для функции y = f(x) одной переменной x условие дифференцируемости имело вид: y = A x + α x = = A x + o(Δx).

Возникает вопрос: Каков аналог слагаемого o(Δx) в случае функции m переменных? Можно предположить, что аналогом будет сумма [o(Δx1) + ... + o(Δxm)]. Но это не верно!

Чтобы дать правильный ответ на поставленный вопрос, обозначим буквой ρ расстояние между точками M(x1, ... , xm) и M (x1 + x1, ... , xm + xm) (рис. 9.8).

Рис. 9.8.

Докажем, что условие (9.5) дифференцируемости функции u = f(x1, ... , xm) в точке M можно записать в виде

причем слагаемое o(ρ) = 0 при ρ = 0. Обозначим сумму α1 x1 +

+ ... + α x , входящую в правую часть равенства (9.5), бук-

m m

вой h. Если ρ = (Δx1)2 + ... + (Δxm)2 = 0, то x1 = ... =

Связь дифференцируемости с существованием частных производных. Для функции одной переменной y = f(x) су-

ществование производной в точке x0 является необходимым и достаточным условием дифференцируемости функции в точке x0. Для функции многих переменных существование частных производных в точке M0 уже не является достаточным условием

ее дифференцируемости в этой точке.

Теорема 14 (необходимое условие дифференцируемости функции). Если функция u = f(x1, ... , xm) дифференцируема в

точке M(x1, ... , xm), то она имеет в точке M частные производные по всем переменным.

Доказательство. Запишем условие дифференцируемости функции в точке M в виде (9.5):

Отметим, что обратное к теореме 14 утверждение не верно.

Пример.

u(x, y) =

1 на осях координат, 0 в остальных точках.

∂u∂x(0, 0) = ∂u∂y (0, 0) = 0 (это было показано ранее), но функция u(x, y) не является непрерывной в точке O(0, 0), а потому не

дифференцируема в точке O(0, 0).

Таким образом, существование частных производных — только необходимое, но не достаточное условие дифференцируемости функции в данной точке.

Теорема 15 (достаточное условие дифференцируемости функции). Если функция u = f(x1, ... , xm) имеет частные про-

изводные по всем переменным в некоторой ε-окрестности точки M(x1, ... , xm), причем в самой точке M эти частные производные непрерывны, то функция дифференцируема в точке M.

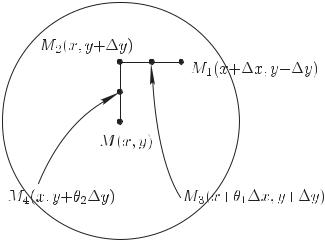
Доказательство. Проведем доказательство теоремы для функции двух

переменных u = f(x, y)

(для сокращения записи). Пусть частные про-

изводные fx и fy существуют в ε-окрестности точки M(x, y) и непре-

рывны в самой точке M. Возьмем x и y

ε-окрестности точки M, и рассмотрим полное приращение функции в точке M:

u = f(x + x, y + y) − f(x, y) =

= [f(x + x, y + y) − f(x, y + y)] + [f(x, y + y) − f(x, y)] =

где 0 < θi < 1, i = 1, 2.

К разностям в квадратных скобках мы применили формулу

Лагранжа конечных приращений, при этом производные fx и fy берутся в промежуточных точках M3 и M4 (рис. 9.9).

Так как по условию теоремы fx и fy непрерывны в точке M(x, y), то fx(x + θ1 x, y + y) = fx(x, y) + α1, fy(x, y +

то есть выполнено условие дифференцируемости функции f(x, y) в виде (9.7). Теорема 15 доказана.

Докажите, что u(x, y) имеет частные производные ux и uy во всех точках плоскости, эти частные производные не являются непрерывными в точке O(0, 0), но функция u(x, y) дифференцируема в точке O(0, 0).

Этот пример показывает, что условие теоремы 15 является только достаточным, но не необходимым условием дифференцируемости функции.

2. 1, на осях координат, u(x, y) =

0, во всех остальных точках.

Докажите, что частные производные ux и uy непрерывны в точке O(0, 0). Вместе с тем, эта функция не дифференцируема в точке O(0, 0).

Объясните, почему этот пример не противоречит теореме 15.

Дифференцируемость сложной функции

Рассмотрим сложную функцию z = f (ϕ(u, v), ψ(u, v)), то есть

z = f(x, y), где x = ϕ(u, v), y = ψ(u, v).

Теорема 16. Пусть:

1.функции x = ϕ(u, v), y = ψ(u, v) дифференцируемы в точке

(u0, v0);

2.функция z = f(x, y) дифференцируема в точке (x0, y0), где

x0 = ϕ(u0, v0), y0 = ψ(u0, v0).

Тогда сложная функция z = f (ϕ(u, v), ψ(u, v)) дифференцируема

в точке (u0, v0).

Доказательство. Дадим произвольные приращения u и v аргументам u и v в точке (u0, v0). Функции x = ϕ(u, v) и y = ψ(u, v)

Этим приращениям x и y соответствует приращение z функции z = f(x, y) в точке (x0, y0), которое в силу условия 2 можно записать в виде

числа, а

α = ∂f∂x α1 + ∂f∂y β1 + ∂ϕ∂u γ1 + ∂ψ∂u γ2 + γ1α1 + γ2β1

и

β = ∂f∂x α2 + ∂f∂y β2 + ∂ϕ∂v γ1 + ∂ψ∂v γ2 + γ1α2 + γ2β2 —

функции, удовлетворяющие, очевидно, условиям

z = f (ϕ(u, v), ψ(u, v)) дифференцируема в точке (u0, v0). Теорема доказана.

Из равенства (9.10) следуют формулы для производных сложной функции:

∂u∂z (u0, v0) = ∂f∂x (x0, y0) · ∂ϕ∂u (u0, v0) + ∂f∂y (x0, y0) · ∂ψ∂u (u0, v0), ∂v∂z (u0, v0) = ∂f∂x (x0, y0) · ∂ϕ∂v (u0, v0) + ∂f∂y (x0, y0) · ∂ψ∂v (u0, v0).