
семестр 6 / задания / высшая математика 2 / задание 6
.docx
М ИНИСТЕРСТВО
НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ
ФЕДЕРАЦИИ
ИНИСТЕРСТВО
НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ
ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
(наименование института полностью)
Кафедра /департамент /центр1 институт химии и энергетики
(наименование кафедры/департамента/центра полностью)
13.03.02 Электроэнергетика и электротехника
(код и наименование направления подготовки, специальности)
(направленность (профиль) / специализация)
Практическое задание №__6_
по учебному курсу «_Высшая математика 2__________»
(наименование учебного курса)
Вариант _10___ (при наличии)
Студент |
Яшин И.А. (И.О. Фамилия) |
|
Группа |
ЭЭТбп-1801а (И.О. Фамилия) |
|
Преподаватель |
Крылова Светлана Александровна (И.О. Фамилия) |
|
Тольятти 2021
Задание №6
№ п/п |
Задача |
Ответ |
|
а) |
Составить
уравнение линии уровня
|
|
|
|
Условие задачи:
|
||
|
Подробное решение:
Центром О(-1:-1) |
|
|
|
График:
|
|
|
б) |
Вычислить
с помощью градиента производную
скалярного поля
|
1 |
|
Условие задачи:
|
|||
|
Подробное решение: Градиентом функции z = f(x,y) называется вектор, координатами которого являются частные производные данной функции, т.е.
Находим частные производные:
Тогда величина градиента равна:
Модуль grad(z) - наибольшая скорость возрастания функции:
Направление вектора-градиента задаётся его направляющими косинусами:
Найдем
производную в точке А по
Найти направление вектора - значит найти его направляющие косинусы:
Модуль
вектора
тогда направляющие косинусы:
Для вектора имеем:
заданная функция в направлении вектора a возрастает |
|
|
1 Оставить нужное

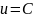 и построить её график:
и построить её график: C=7
C=7





 в точке A
по направлению вектора
в точке A
по направлению вектора
 :
:













 равен:
равен:

