9.3. Анализ эффективности инновационных проектов

В условиях рыночных отношений при разработке и внедре­нии нововведений наиболее распространенным является не нормативный, а именно проектный подход. В его основе лежит принцип денежных потоков (cash flow). Целесообразно ис­пользовать следующие основные показатели эффективности инновационного проекта:

• финансовая (коммерческая) эффективность, учитывающая финансовые последствия для участников проекта;

• бюджетная эффективность, учитывающая финансовые по­следствия для бюджетов всех уровней;

480

• народнохозяйственная экономическая эффективность, учи­ тывающая затраты и результаты, выходящие за пределы прямых финансовых интересов участников проекта и допус­ кающие стоимостное выражение.

В основе оценки эффективности инновационного проекта лежит сравнительный анализ объема предполагаемых инвес­тиций и будущих денежных поступлений. Сравниваемые ве­личины в большинстве случаев относятся к различным вре­менным периодам. Отсюда вытекает необходимость сопостав­ления доходов и затрат и приведения их в сопоставимый вид.

В общем виде критерии, используемые в анализе эффек­тивности инновационных проектов, можно подразделить на две группы в зависимости от того, учитывается или нет вре­менной параметр:

• основанные на учетных оценках (без дисконтирования);

• основанные на дисконтированных оценках.

К первой группе относятся критерии:

• срок (период) окупаемости (РР);

• коэффициент эффективности (ARR);

• коэффициент покрытия долга (DCR).

Ко второй группе относятся критерии:

• чистый приведенный эффект (NPV);

• индекс рентабельности (РI);

• внутренняя норма рентабельности (IRR);

• модифицированная внутренняя норма рентабельности (MIRK);

• дисконтированный срок окупаемости (DPP).

Метод определения срока окупаемости инвестиций в инно­вационные проекты (РР) следует признать одним из самых простых. Он не предполагает временной упорядоченности де­нежных поступлений и может быть широко распространен­ным в аналитической практике. Алгоритм расчета срока оку­паемости (РР) зависит от равномерности распределения про­гнозируемых доходов от инвестиций в инновационные проек­ты. Если доход распределен по годам равномерно, то срок окупаемости рассчитывается делением единовременных за­трат на величину годового дохода, обусловленного ими. При получении дробного числа оно округляется в сторону увеличе-

481

ния до ближайшего целого. Если прибыль распределена не­равномерно, то срок окупаемости рассчитывается прямым подсчетом лет, в течение которых инвестиция в инновацию бу­дет погашена кумулятивным доходом.

В наиболее общем виде указанный инвестиционный про­ект Р представляет собой такую модель (используется алго­ритмизация, принятая в странах с развитой рыночной эконо­микой):

где 1С_i - инвестиция в инновацию в i-м году, i = 1, 2, 3,..., т

(чаще всего считается, что т = 1); CF_k - приток (отток) денеж­ных средств в k-м году, где k =1, 2, 3, ..., п; п - продолжитель­ность проекта; r - коэффициент дисконтирования. Общая формула расчета показателя РР имеет вид:

Если же при исчислении показателя РР учитывается вре­менной аспект, то в этом случае в расчет принимаются денеж­ные потоки, дисконтированные по показателю «цена» аванси­рованного капитала (СС), а формула для расчета дисконтиро­ванного срока окупаемости (DPP) принимает вид:

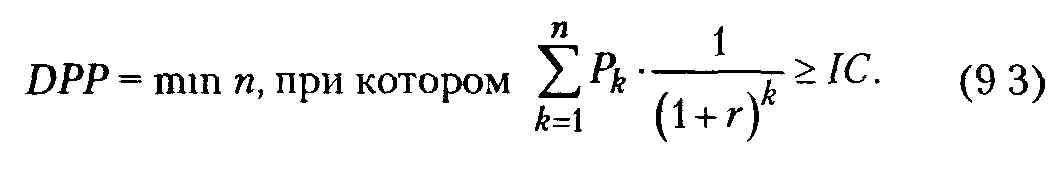
В случае дисконтирования срок окупаемости увеличивает­ся, те всегда DPP> РР Иначе говоря, инновационный проект, приемлемый по критерию РР, может оказаться неприемлемым по критерию DPP.

Проиллюстрируем это на простом примере Прежде всего отметим, что в оценке инвестиционных проектов критерии РР и DPP могут использоваться двояко.

• проект принимается, если окупаемость имеет место,

482

• проект принимается только в том случае, если срок окупае­мости не превышает установленного в компании некоторого лимита.

Пример.

Компания рассматривает целесообразность принятия проекта с денеж­ным потоком, приведенным в гр 2 табл 9.10. Цена капитала компании 12% Как правило, проекты со сроком погашения, превышающем 4 года, не прини­маются. Требуется сделать анализ с помощью критериев обыкновенного и дисконтированного сроков окупаемости.

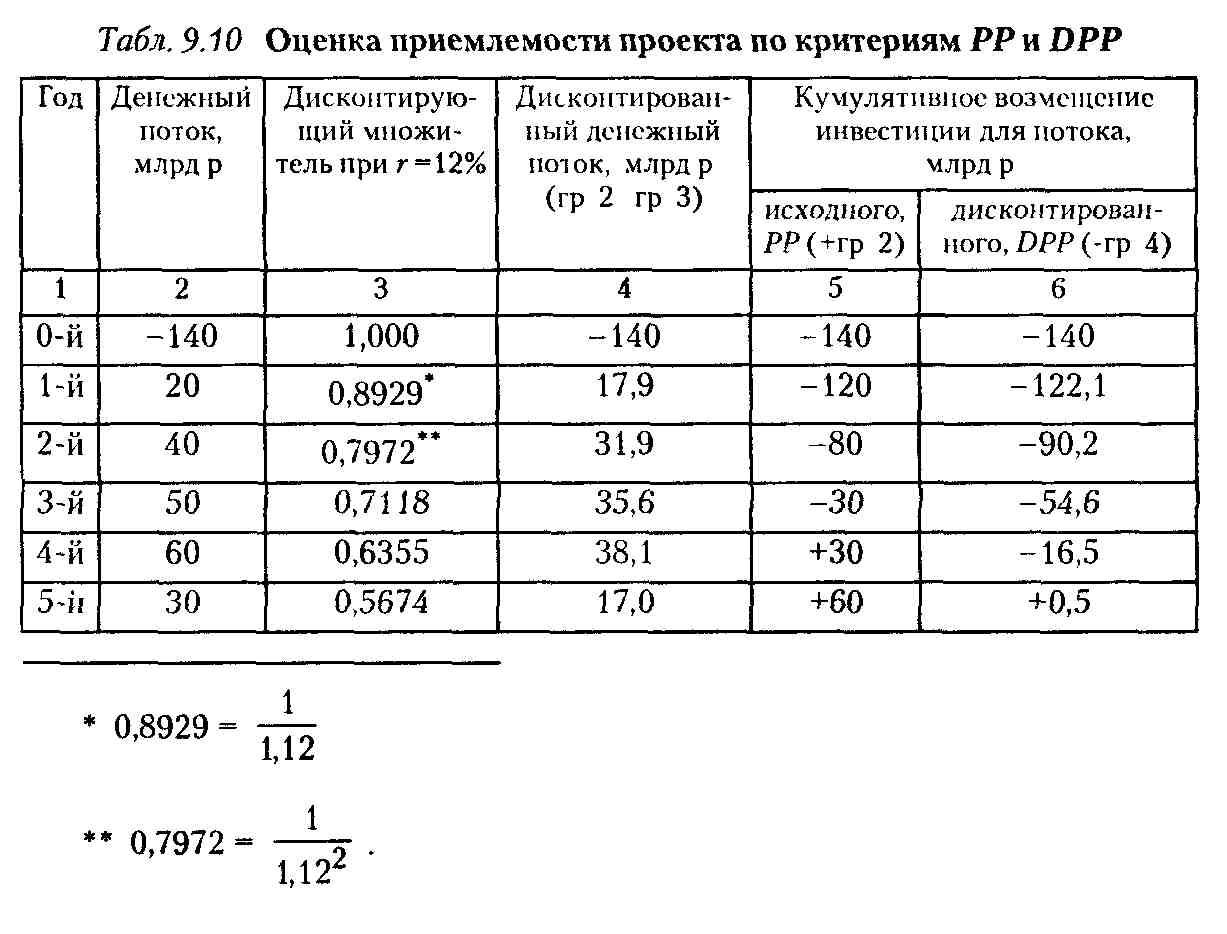
Из приведенных в табл. 9.10 расчетов видно, что РР - 4 го­дам (при точном расчете РР = 3,5 года), a DPP = 5 годам (при точном расчете DPP = 4,9 года). Таким образом, если решение принимается на основе обыкновенного срока окупаемости, то проект приемлем, если используется критерий дисконтиро­ванного срока окупаемости, то проект скорее всего будет от­вергнут.

Показатель срока окупаемости инвестиции в инновацию очень прост в расчетах, вместе с тем он имеет ряд недостатков, которые необходимо учитывать при проведении анализа.

Во-первых, он не учитывает влияние доходов последних периодов. В качестве примера рассмотрим два проекта с оди-

483

наковыми капитальными затратами (13 млрд р.), но различны­ми прогнозируемыми годовыми доходами: по проекту А - 5,3 млрд р. в течение трех лет; по проекту Б - 4,8 млрд р. в течение десяти лет. Оба эти проекта в течение первых трех лет обеспе­чивают окупаемость капитальных вложений, поэтому с пози­ции данного критерия они равноправны. Однако очевидно, что проект Б гораздо более выгоден.

Во-вторых, поскольку этот метод основан на недисконти-рованных оценках, то он не делает различия между проектами с одинаковой суммой кумулятивных доходов, но различным распределением ее по годам. Так, с позиции этого критерия проект А с годовыми доходами 60, 80, 40 млрд р. и проект Б с годовыми доходами 40, 60, 80 млрд р. равноправны, хотя оче­видно, что первый проект более предпочтителен, поскольку обеспечивает большую сумму доходов в первые два года. Эти дополнительные средства могут быть направлены в оборот и в свою очередь принесут новые доходы.

В-третьих, данный метод не обладает свойствами аддитив­ности. Рассмотрим ситуацию, приведенную в табл. 9.11.

Табл 911 Динамика денежных потоков

Год	Денежные потоки но проектам (vi прд р)
	А	Б	В	А и В	Б и В
0-й	-50	-50	-50	-100	-100
1-й	0	50	0	0	50
2-й	100	0	0	100	0
3-й	25	75	75	100	150
Период окупаемости, лет	2,5	1,5	3,5	2,5	3,5

Допустим, что проекты А и Б являются взаимоисключаю­щими, а проект В - независимым. Это означает, что если у предприятия имеются финансовые возможности, то оно мо­жет выбрать не только какой-то один из представленных про­ектов, но и их комбинации, т.е. проекты А и В или проекты Б и В. Если рассматривать каждый проект отдельно с применени­ем показателя «период окупаемости», то можно сделать вывод, что предпочтительным является проект Б. Однако если рас­сматривать комбинации проектов, то следует предпочесть комбинацию из худших проектов А и В.

484

В то же время существует ряд ситуаций, при которых при­менение метода, основанного на расчете срока окупаемости за­трат, может быть целесообразным. В частности, это ситуация, когда руководство предприятия в большей степени озабочено решением проблемы ликвидности, чтобы инвестиции в инно­вацию окупились и как можно скорее. Метод также хорош в ситуации, когда инвестиции сопряжены с высокой степенью риска, поэтому чем короче срок окупаемости, тем менее риско­ванным является проект. Такая ситуация характерна для от­раслей или видов деятельности, которым присуща большая ве­роятность достаточно быстрых технологических изменений. Таким образом, критерий РР позволяет получить оценки, хотя и грубые, о ликвидности и рисковости инвестиционного про­екта в инновацию. Понятие ликвидности проекта является ус­ловным. Считается, что из двух проектов более ликвиден тот, у которого меньше срок окупаемости. При сравнительной оцен­ке рисковости проектов с помощью критерия РР рассуждаем так: денежные поступления удаленных от начала реализации проекта лет трудно прогнозируемы, т.е. они более рисковы по сравнению с поступлениями первых лет, поэтому из двух про­ектов менее рисковым является тот, у которого меньше срок окупаемости.

Метод расчета коэффициента эффективности инвестиции в инновацию (ARR) имеет две характерные черты:

• он не предполагает дисконтирования показателей дохода;

• доход характеризуется показателем чистой прибыли PN.

Алгоритм расчета исключительно прост, что обусловлива­ет возможность широкого использования этого показателя на практике: коэффициент эффективности (ARR) рассчитывает­ся делением среднегодовой прибыли PN на среднюю величину инвестиции в инновацию (коэффициент берется в процентах). Средняя величина инвестиции в инновацию находится деле­нием исходной суммы капитальных вложений на 2, если пред­полагается, что по истечении срока реализации анализируемо­го проекта все капитальные затраты будут списаны. Если же допускается наличие остаточной или ликвидационной стои­мости (RV), то ее оценка должна быть исключена:

485

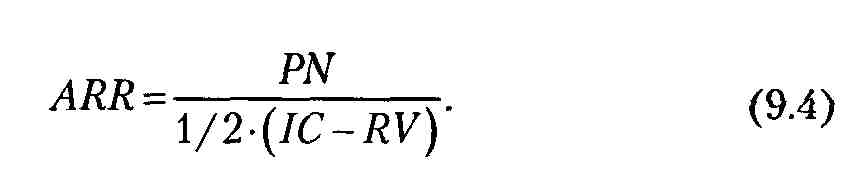
Данный показатель сравнивается с коэффициентом рента­бельности авансированного капитала, рассчитываемого деле­нием общей суммы прибыли предприятия на общую сумму средств, авансированных в его деятельность (среднюю).

В принципе, возможно и установление специального поро­гового значения, с которым будет сравниваться ARR, или даже их системы, дифференцированной по видам проектов, степени риска, центрам собственности и др.

Метод, основанный на коэффициенте эффективности ин­вестиции в инновацию, также имеет ряд существенных недо­статков, обусловленных в основном тем, что он не учитывает временной компоненты денежных потоков. В частности, метод не предполагает учет различия между проектами с одинаковой суммой среднегодовой прибыли, но варьирующей суммой прибыли по годам, а также между проектами, имеющими оди­наковую среднегодовую прибыль, но генерируемую в течение различного количества лет и т.п.

Метод расчета чистого приведенного эффекта (NPV) осно­ван на сопоставлении величины исходной инвестиции (1С) в инновацию с общей суммой дисконтированных чистых денеж­ных поступлений, генерируемых ею в течение прогнозируемо­го срока. Поскольку приток денежных средств распределен во времени, то он дисконтируется с помощью коэффициента г, устанавливаемого аналитиком (инвестором) самостоятельно исходя из ежегодного процента возврата, который он хочет или может иметь на инвестируемый им капитал.

Допустим, делается прогноз, что инвестиция (IС) будет гене­рировать в течение п лет годовые доходы в размере P₁, Р₂ , Р₃, ..., Р_n-Общая накопленная величина дисконтируемых доходов (PV) и чистый приведенный эффект (NPV) соответственно рассчи­тываются по формулам (9.5) и (9.6):

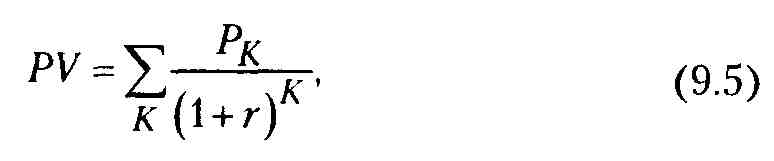
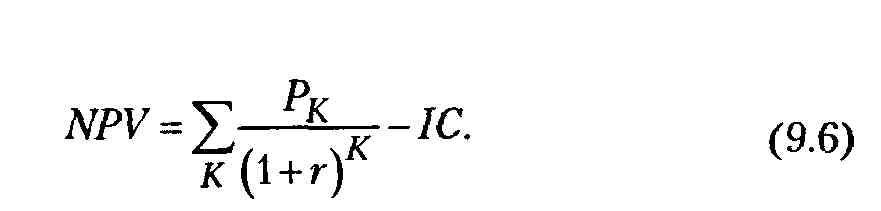
Очевидно, что если:

NPV> О, то инновационный проект следует принять;

NPV< О, то инновационный проект следует отвергнуть;

NPV = 0, то инновационный проект ни прибыльный, ни убыточный.

При прогнозировании доходов по годам необходимо, по возможности, учитывать все виды поступлений как произ­водственного, так и непроизводственного характера, которые могут быть ассоциированы с данным инновационным проек­том. Так, если по окончании периода реализации проекта пла­нируется поступление средств в виде ликвидационной стои­мости оборудования или высвобождения части оборотных средств, то они должны быть учтены как доходы соответству­ющих периодов.

Если проект предполагает не разовую инвестицию в инно­вацию, а последовательное инвестирование финансовых ре­сурсов в течение т лет, то формула для расчета чистого приве­денного эффекта модифицируется следующим образом:

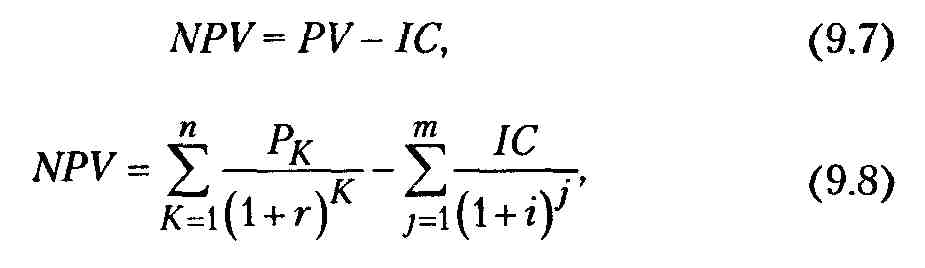
где i - прогнозируемый средний уровень инфляции.

Расчет с помощью приведенных формул вручную достаточ­но трудоемок, поэтому для удобства применения этого и дру­гих методов, основанных на дисконтированных оценках, целе­сообразно разрабатывать и использовать специальные статис­тические таблицы, в которых табулируются значения сложных процентов, дисконтирующих множителей, дисконтированного значения денежной единицы и т.п. в зависимости от временно­го интервала и значения коэффициента дисконтирования.

При расчете чистого приведенного эффекта NPV, как прави­ло, используется постоянная ставка дисконтирования, однако при некоторых обстоятельствах, например, ожидается измене-

487

ние уровня учетных ставок, могут использоваться индивидуа­лизированные по годам коэффициенты дисконтирования Ес­ли в ходе имитационных расчетов приходится применять раз­личные коэффициенты дисконтирования, то, во-первых, фор­мула (9 6) неприменима и, во-вторых, проект, приемлемый при постоянной дисконтной ставке, может стать неприемлемым.

Пример

Требуется проанализировать инвестиционный проект в инновацию со следующими характеристиками (млрд р ) - 156,40, 70, 70, 50

Рассмотрим два случая а) цена капитала - 13%, 6) ожидается, что цена ка­питала будет меняться по годам следующим образом 11%, 12%, 13%, 14%

а) Воспользуемся формулой 9 6

В этом случае инвестиционный проект в инновацию неприемлем

Показатель чистого приведенного эффекта отражает про­гнозную оценку изменения экономического потенциала пред­приятия в случае принятия рассматриваемого инвестицион­ного проекта в инновацию Этот показатель аддитивен во вре­менном аспекте, т.е. чистые приведенные эффекты различных проектов можно суммировать. Это очень важное свойство, вы­деляющее этот критерий из всех остальных и позволяющее ис­пользовать его в качестве основного при анализе оптимальнос­ти инвестиционного портфеля в инновационные проекты

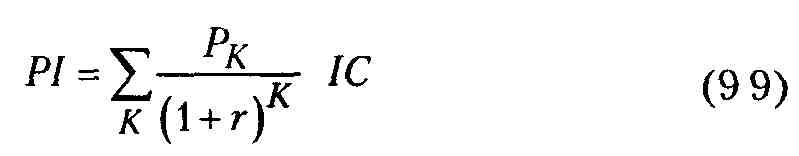
Очевидно, что если

PI > 1, то инновационный проект следует принять,

488

Метод расчета индекса рентабельности инвестиции в инно­вацию является следствием метода расчета чистого приведен­ного эффекта Этот индекс рентабельности (РГ) рассчитывает­ся по формуле:

PI< 1, то инновационный проект необходимо отвергнуть;

Р1= 1, то инновационный проект не является ни прибыль­ным, ни убыточным.

В отличие от чистого приведенного эффекта индекс рента­бельности является относительным показателем. Благодаря этому он очень удобен при выборе одного проекта из ряда аль-| тернативных, имеющих примерно одинаковые значения чис­тых приведенных эффектов (в частности, если два инноваци­онных проекта имеют одинаковые значения чистых приведен­ных эффектов, но разные объемы требуемых инвестиций, то очевидно, что выгоднее тот из них, который обеспечивает большую эффективность вложений), либо при комплектова­нии портфеля инвестиций в инновации с максимальным сум­марным значением чистых приведенных эффектов.

В методе расчета внутренней нормы рентабельности инвес­тиции в инновацию (IRR) под указанной нормой рентабель­ности понимают значение коэффициента дисконтирования r, при котором NPV проекта равен нулю:

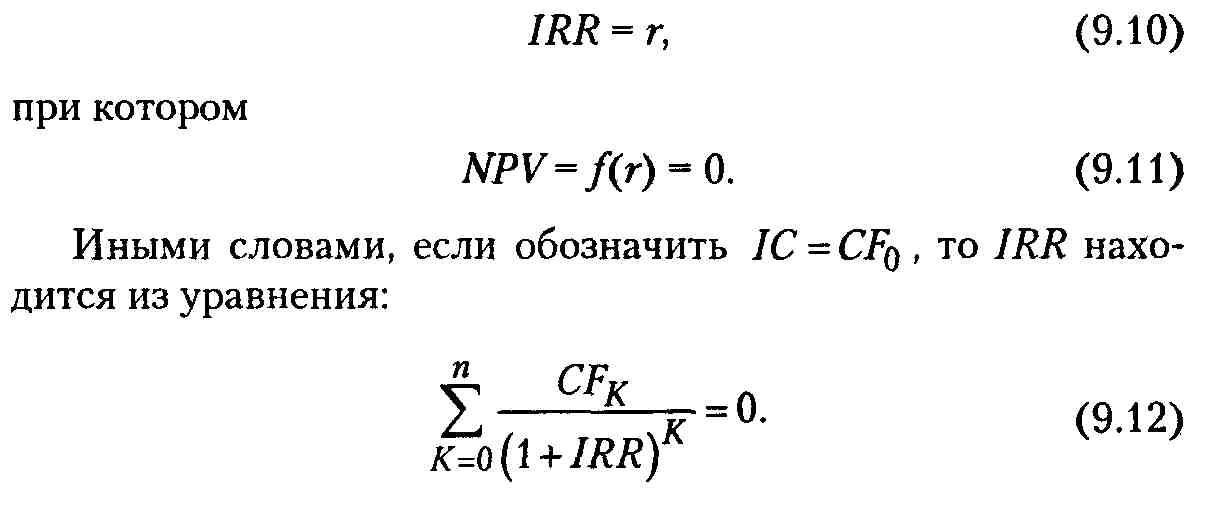
Смысл расчета этого коэффициента при анализе эффектив­ности планируемых инвестиций в инновацию заключается в следующем: IRR показывает ожидаемую доходность проекта, а следовательно, максимально допустимый относительный уро­вень расходов, которые могут быть ассоциированы с данным проектом Например, если проект полностью финансируется за счет ссуды коммерческого банка, значение IRR показывает верх­нюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.

На практике любое предприятие финансирует свою де­ятельность, в том числе и инновационную, из различных ис-

489

точников, в частности из внешних. В качестве платы за пользо­вание авансированными в деятельность предприятия финан­совыми ресурсами оно уплачивает проценты, дивиденды, воз­награждения и т.п., т.е. несет некоторые обоснованные расходы на поддержание своего экономического потенциала. Показатель, характеризующий относительный уровень этих расходов, можно назвать «ценой» авансированного капитала (СО- Этот показатель отражает сложившийся на предпри­ятии минимум возврата на вложенный в его деятельность ка­питал, его рентабельность и рассчитывается по формуле сред­ней арифметической взвешенной.

Экономический смысл этого показателя заключается в сле­дующем: предприятие может принимать любые решения ин­вестиционного характера в инновацию, уровень рентабельнос­ти которых не ниже текущего значения показателя СС {пли це­ны источника средств для данного проекта, если он имеет це­левой источник). Именно с ним сравнивается показатель IRR, рассчитанный для конкретного проекта. Эта связь будет сле­дующей: если IRR > СС, то инновационный проект следует принять; IRR < СС, то инновационный проект следует отвергнуть; IRR = СС, то инновационный проект не является ни прибыль­ным, ни убыточным.

Практическое применение данного метода осложнено, если в распоряжении аналитика нет специализированного финан­сового калькулятора. В этом случае применяется метод после­довательных операций с использованием табулированных значений дисконтирующих множителей. Для этого с помощью таблиц выбираются два значения коэффициента дисконтиро­вания r₁ < r₂ таким образом, чтобы в интервале (r₁, r₂) функция NPV = f(r) меняла свое значение с «+» на«-» или с «-» на «+». Далее применяют формулу

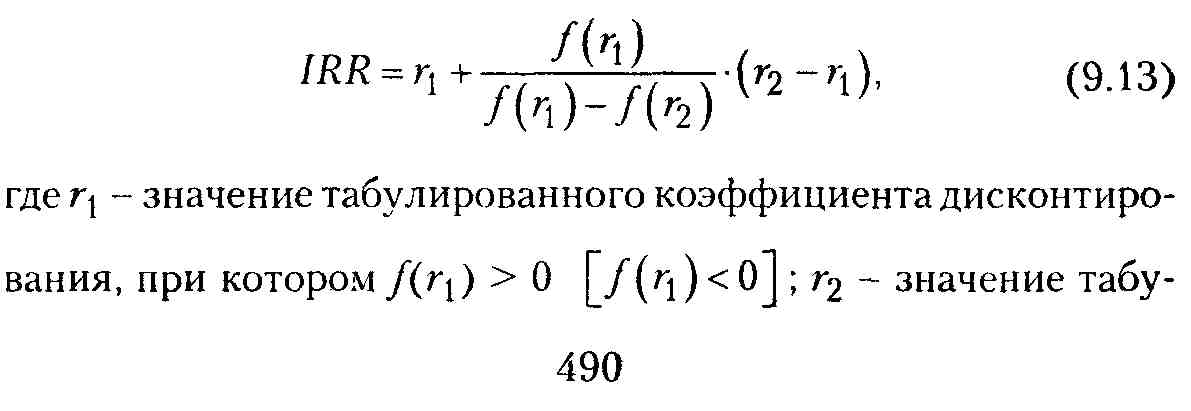
Требуется рассчитать значение показателя IRR для инвес­тиционного проекта в инновацию, рассчитанного на три года, требующего инвестиций в размере 12 млрд р. и имеющего предполагаемые денежные поступления в размере 4 млрд р., 5 млрд р., 8 млрд р.

Возьмем два произвольных значения коэффициента дискон­тирования: r = 9%, r= 19%. Соответствующие расчеты с исполь­зованием табулированных значений на основе формул 9.5-9.7 приведены в табл. 9.12.

Можно уточнить полученное значение. Допускаем, что пу­тем нескольких итераций мы определили ближайшие целые значения коэффициента дисконтирования, при которых NPV меняет знак

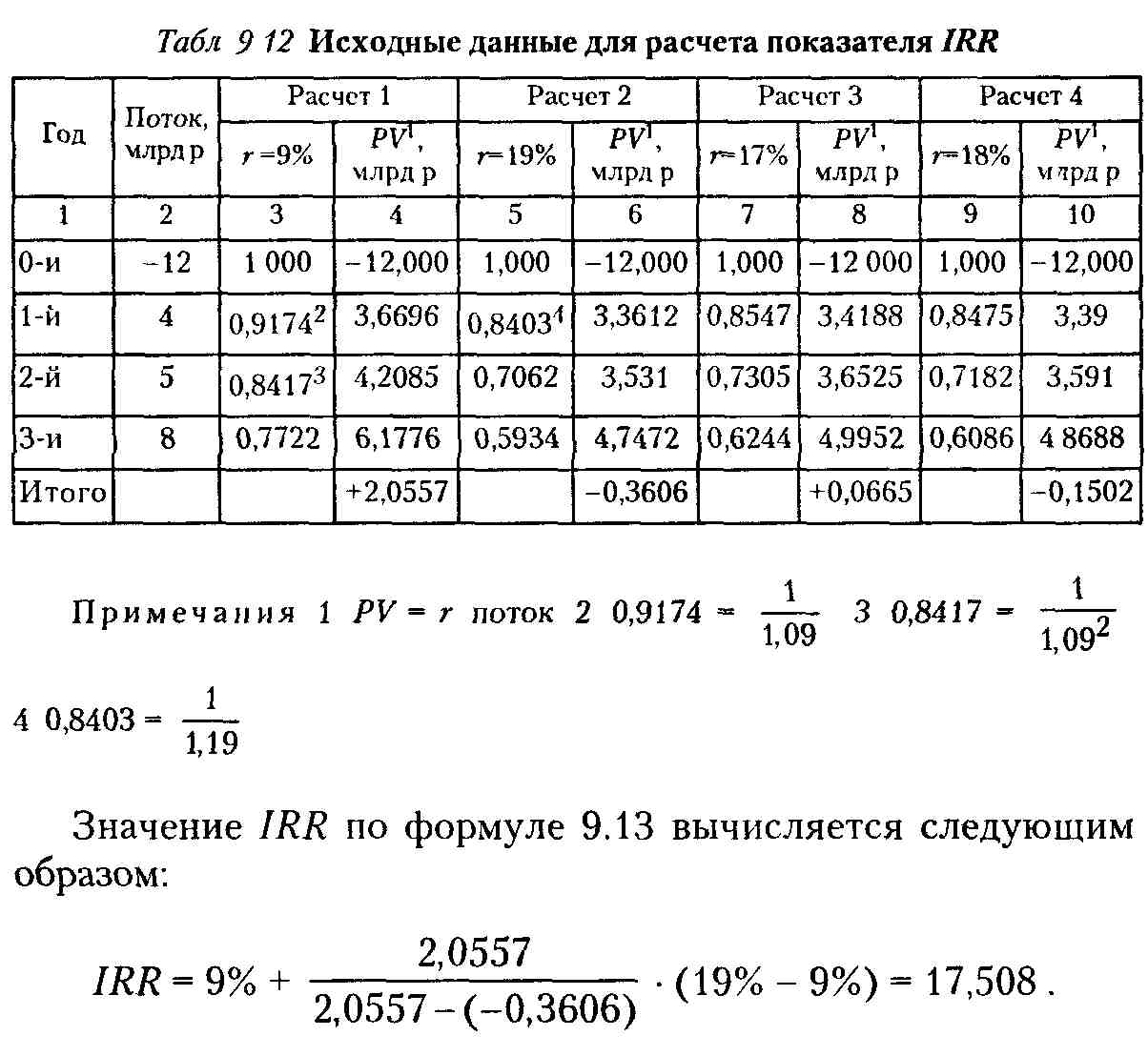
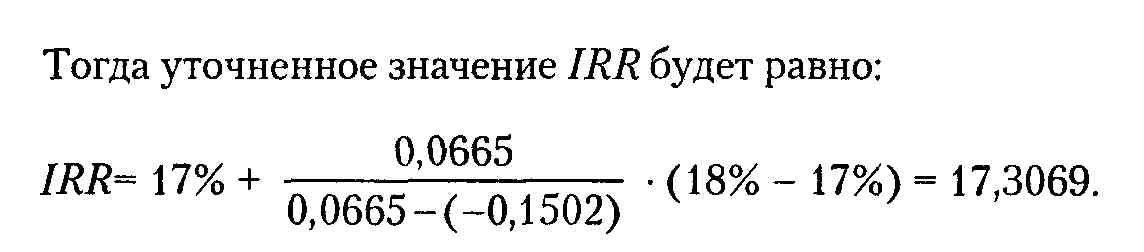
Как видим, метод последовательных итераций обеспечива­ет весьма высокую точность (отметим, что с практической точ­ки зрения такая точность является излишней). Свод всех вы­числений приведен в табл. 9.12. Рассмотренная методика применима лишь к акционерным об­ществам. На предприятиях, не являющихся акционерными, анало­гом показателя СС является уровень издержек производства и об­ращения в процентах к общей сумме авансированного капитала

Между показателями NPV, PI, IRR, СС имеются следующие взаимосвязи:

если NPV> О, то одновременно IRR > СС и Р1>1;

если NPV< 0, то одновременно IRR< СС и Р1< 1;

если NPV = 0, то одновременно IRR = СС и Р1= 1.

Основной недостаток, присущий внутренней норме рента­бельности инвестиции в инновацию (IRR) в отношении оцен­ки проектов с неординарными денежными потоками, не явля­ется критическим и может быть преодолен. Соответствующий аналог IRR, который может применяться при анализе любых проектов, называется модифицированной внутренней нормой рентабельности инвестиции в инновацию (MIRR). Алгоритм расчета предусматривает выполнение нескольких процедур. Прежде всего рассчитываются суммарная дисконтированная стоимость всех оттоков и суммарная наращенная стоимость всех притоков, причем и дисконтирование и наращение осу­ществляются по цене источника финансирования проекта. На­ращенная стоимость притоков называется терминальной сто­имостью. Затем определяется ставка дисконтирования, урав­нивающая суммарную приведенную стоимость оттоков и тер­минальную стоимость, которая в данном случае как раз и представляет собой MIRR Общая формула расчета имеет вид:

где 0F_i - отток денежных средств в i-м периоде (по абсолют­ной величине), IF_i - приток денежных средств в i-м периоде; r - стоимость источника финансирования данного проекта в инновацию, п - продолжительность проекта

Формула имеет смысл, если терминальная стоимость пре­вышает сумму дисконтированных оттоков

Критерий модифицированной внутренней нормы рентабель­ности инвестиции в инновацию (MIRR) в полной мере согласу­ется с критерием чистого приведенного эффекта (NPV) и потому может быть использован для оценки независимых проектов Что касается альтернативных проектов, то противоречия между кри­териями NPV и MIRR могут возникать, если проекты существен­но разнятся по масштабу, т е значения элементов у одного пото­ка значительно больше по абсолютной величине, чем у другого, либо проекты имеют различную продолжительность В таком случае целесообразно применять критерий NPV, не забывая од­новременно об учете рисковости денежного потока

В реальной жизни вполне вероятна ситуация, когда необходи­мо сравнивать инвестиционные проекты в инновацию различной продолжительности Речь идет как о независимых, так и об альтер­нативных проектах В частности, сравнение независимых проек­тов может иметь место, когда заранее не известен объем доступных источников финансирования В этом случае проводится ранжиро­вание проектов по степени их приоритетности, т е они как бы вы­страиваются в очередь - по мере появления финансовых возмож­ностей проекты последовательно принимаются к внедрению

Суммарный чистый приведенный эффект (NPV) повторя­ющегося инновационного проекта рассчитывается по формуле

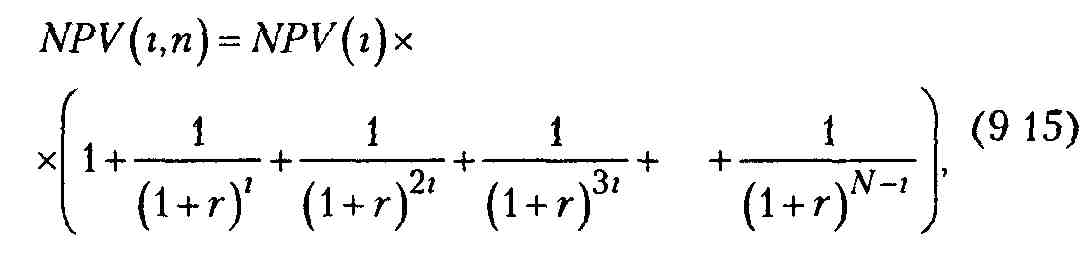
где NPV(i) - чистый приведенный эффект исходного проекта в инновацию, i - продолжительность этого проекта, r - ставка дисконтирования в долях единицы, N - наименьшее общее кратное, п - число повторений исходного проекта (оно харак­теризует число слагаемых в скобках)

493

Данную методику можно упростить в вычислительном плане. Так, если анализируется несколько проектов, сущест­венно различающихся по продолжительности реализации, то расчеты могут быть достаточно утомительными. Их можно уменьшить, если предположить, что каждый из альтернатив­ных проектов может быть реализован неограниченное число раз. В этом случае при п —> oо число слагаемых в формуле рас­чета NPV (t, п) будет стремиться к бесконечности, а значение NPV(t, оо) может быть найдено по известной формуле для бес­конечно убывающей геометрической прогрессии:

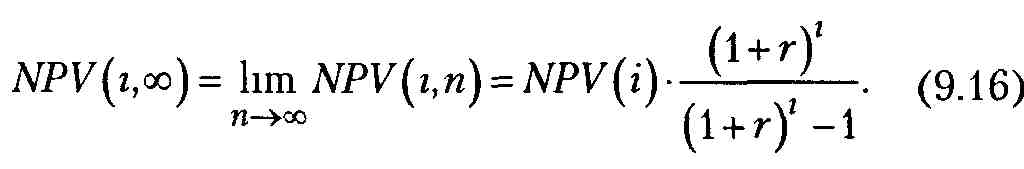
Из двух сравниваемых инвестиционных проектов в инно­вацию проект, имеющий большее значение NPV(i, со), являет­ся предпочтительным.

Существует также и такой подход. Рассчитывают чистый приведенный эффект (NPV) однократной реализации каждого проекта. Для каждого проекта находят эквивалентный срочный аннуитет (будущую стоимость FV_pst исходного денежного пото­ка), приведенная стоимость которого в точности равна NPVnpo-екта. При этом считается, что генерируемые в рамках одного временного периода поступления имеют место либо в его нача­ле, либо в его конце, т.е. они не распределены внутри периода, а сконцентрированы на одной из его границ. В первом случае по­ток называется потоком пренумерандо, или авансовым, во вто­ром - потоком постнумерандо. Наращенный денежный поток C₁, С₂, Сз,..., С„ для исходного потока постнумерандо имеет вид:

а будущая стоимость FV_pst исходного денежного потока (ан­нуитета) постнумерандо может быть оценена как сумма нара­щенных поступлений, иными словами^-

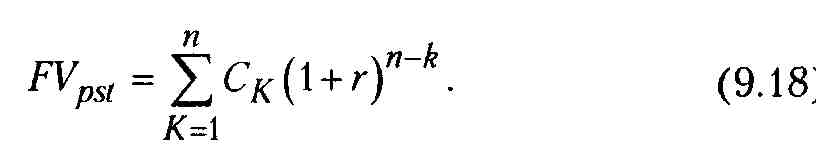
В обратной задаче подразумевается оценка с позиции теку­щего момента, т.е. на конец периода 0. В этом случае реализуется схема дисконтирования, а расчеты необходимо вести по приве­денному потоку. Элементы приведенного денежного потока уже можно суммировать. Их сумма характеризует приведенную, или текущую, стоимость денежного потока, которую при необходи­мости можно сравнивать с величиной первоначальной инвести­ции в инновацию. Следовательно, приведенный денежный по­ток для исходного потока постнумерандо будет иметь вид:

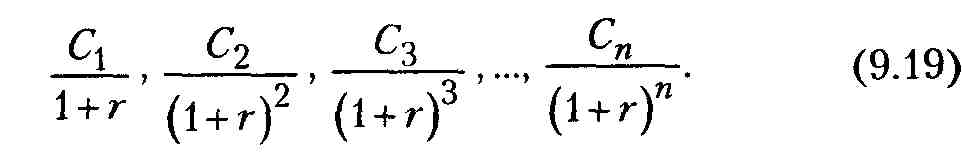
Приведенная стоимость денежного потока постнумерандо PV_pst в общем случае рассчитывается по формуле

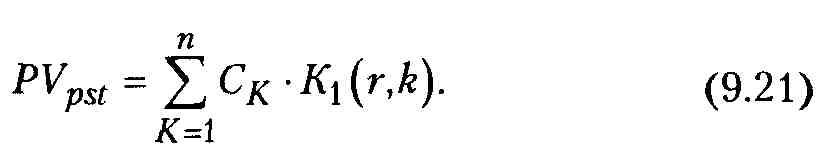
Множитель K\(r,k} называется дисконтирующим множи­телем для единичного платежа и определяется по формуле

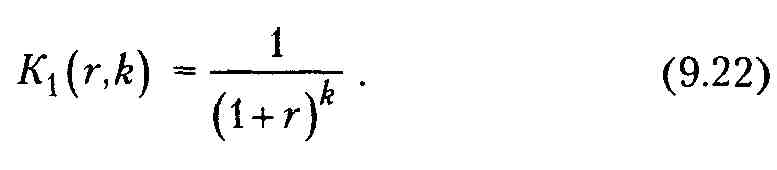
Если использовать дисконтирующий множитель, то фор­мулу (9. 20) можно записать следующим образом:

Он показывает на текущий момент цену одной денежной единицы будущего, т.е. чему равна одна денежная единица (на­пример, один рубль), циркулирующая в сфере бизнеса k пери­одов от момента расчета при заданной процентной ставке (до­ходности) г и частоте начисления процента.

Общая формула для оценки текущей стоимости срочного аннуитета постнумерандо PV^a_pst выводится из формулы 9.20 и имеет вид:

495

Множитель K₂(r,n) называется дисконтирующим множи­телем для аннуитета или коэффициентом дисконтирования ренты (аннуитета) и как сумма членов геометрической про­грессии равен величине:

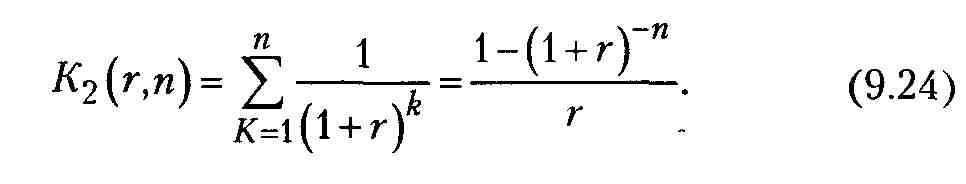
Экономический смысл дисконтирующего множителя K₂(r,n) заключается в том, что он показывает, чему равна с позиции текущего момента величина аннуитета (он пред­ставляет собой частный случай денежного потока или финан­совую ренту) с регулярными денежными поступлениями в размере одной денежной единицы (например, один рубль), продолжающегося п равных периодов с заданной процентной

ставкой r. Дисконтирующий множитель К₂(r,п) полезно ин­терпретировать и как величину капитала, поместив который в банк под сложную процентную ставку г можно обеспечить регулярные выплаты в размере одной денежной единицы в течение п периодов (выплаты производятся в конце каждого периода).

Таким образом, величина аннуитетного платежа (ЕАА) рас­считывается с помощью формулы 9.23. Предполагая, что най­денный аннуитет может быть заменен бессрочным аннуитетом с той же самой величиной аннуитетного платежа, рассчитыва­ют приведенную стоимость бессрочного аннуитета PV^a (оо) по формуле

где А - одно денежное поступление за период (например, год); r- ставка начисления процентов.

496

Данная формула показывает, что поток даже с неограни­ченным числом платежей имеет все же конечную приведен­ную стоимость. С финансовой точки зрения это понятно, по­скольку деньги, которые поступят через много лет, сейчас ма­ло что стоят (а при высокой инфляции практически ничего не стоят). Эта же ситуация проявляется и при сравнении коэф­фициентов дисконтирования бессрочного аннуитета и аннуи­тетов с большим сроком. Также эта формула используется для оценки целесообразности приобретения бессрочного аннуите­та, если известен размер денежного поступления за период. В качестве г обычно принимается гарантированная процент­ная ставка (например, процент, предлагаемый государствен­ным банком). Инвестиционный проект в инновацию, имею­щий большее значение PV^a (оо), является предпочтительным.

Методам, основанным на повторе исходных проектов, при­суща определенная условность, заключающаяся в молчаливом распространении исходных условий на будущее, что не всегда корректно. Во-первых, далеко не всегда можно сделать точную оценку продолжительности исходного проекта; во-вторых, не очевидно, что проект будет повторяться п-е число раз, особен­но если он сам по себе достаточно продолжителен; в-третьих, условия его реализации в случае повтора могут измениться (это касается как размера инвестиций в инновацию, так и ве­личины прогнозируемых чистых доходов); в-четвертых, рас­четы во всех рассмотренных методах абсолютно формализова­ны, при этом не учитываются различные факторы, которые яв­ляются либо не формализованными, либо имеют общеэконо­мическую природу (инфляция, научно-технический прогресс, изменение технологий, заложенных в основу исходного проек­та, и др.) и т.п. Поэтому к применению подобных методов нуж­но подходить осознанно в связи с тем, что если исходным па­раметрам сравниваемых проектов свойственна достаточно вы­сокая неопределенность, то можно не принимать во внимание различие в продолжительности их действия и ограничиться расчетом стандартных критериев.

В анализе эффективности инновационных проектов необ­ходимо по возможности (или если целесообразно) учитывать влияние инфляции. Это можно сделать корректировкой на ин­декс инфляции (i) либо будущих поступлений, либо ставки

497

дисконтирования. Наиболее корректной, но и более трудоем­кой в расчетах является методика, предусматривающая кор­ректировку всех факторов, влияющих на денежные потоки сравниваемых проектов. Основными факторами являются пе­ременные расходы и объем выручки. Корректировка может осуществляться с использованием различных индексов, по­скольку индексы цен на продукцию коммерческой организа­ции и потребляемое ею сырье могут существенно отличаться от индекса инфляции. С помощью таких пересчетов исчисляются новые денежные потоки, которые и сравниваются между собой с помощью критерия чистого приведенного эффекта (NPV).

Более простой является методика корректировки ставки дисконтирования на индекс инфляции. Прежде всего рассмот­рим логику такой корректировки на простейшем примере.

Пример.

Предприниматель готов сделать инвестицию в инновацию исходя из 9% годовых Это означает, что 500 млн р в начале года и 545 млн р в конце года имеют для предпринимателя одинаковую ценность Если допустить, что име­ет место инфляция в размере 6% в год, го для того, чтобы сохранить покупа­тельную стоимость полученного в конце i ода денежного поступления 545 млн р., необходимо откорректировать эту величину на индекс инфляции 545 1,06 - 577,7 (млн р )

Таким образом, чтобы обеспечить желаемый доход, предприниматель дол­жен был использовать в расчетах не 9%-и рост капитала, а другой показатель, отличающийся от исходного на величину индекса инфляции

545 1,06 = 577,7

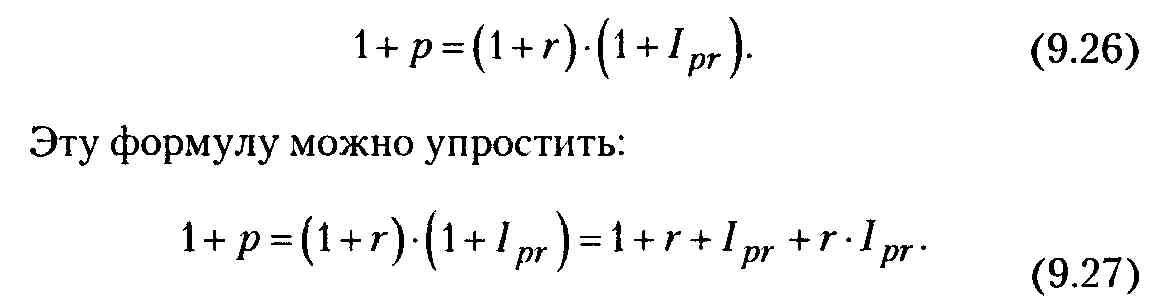
Последним слагаемым ввиду его малости в практических рас­четах пренебрегают, поэтому окончательная формула имеет вид:

Общая формула, связывающая обычную ставку дисконтиро­вания (r), применяемую в условиях инфляции, номинальный ко­эффициент дисконтирования (р) и индекс инфляции (I_pr) такова:

Пример.

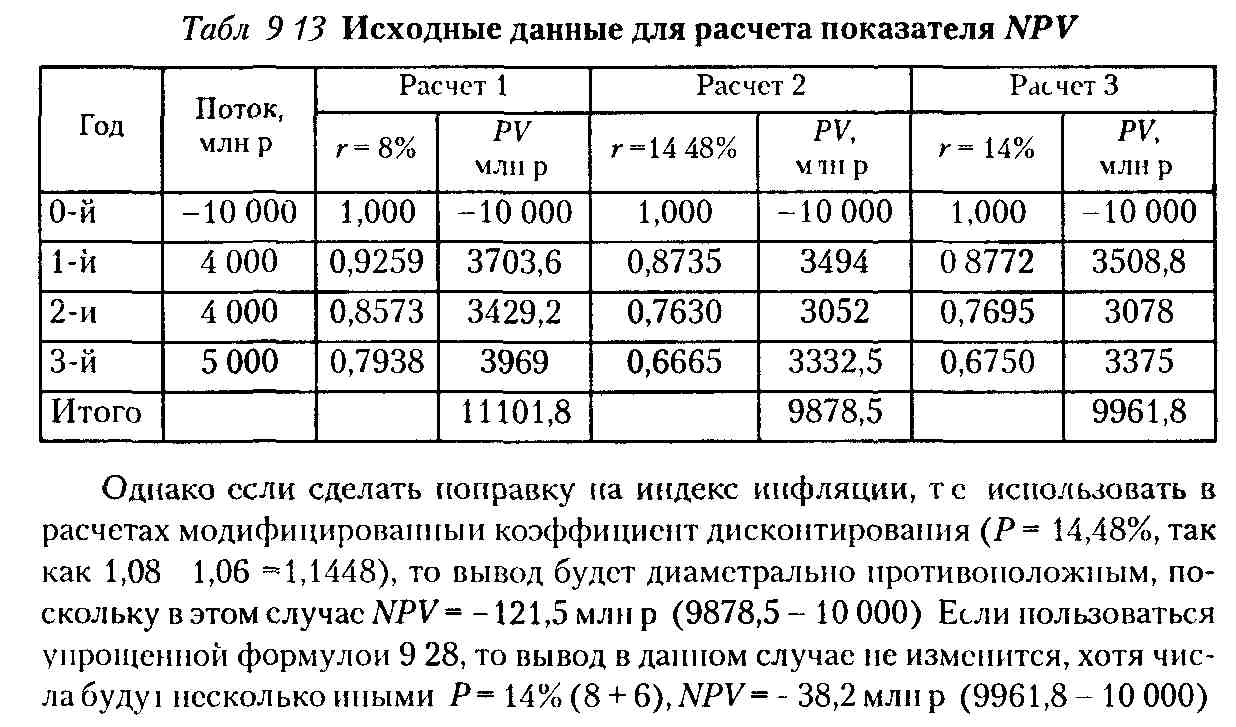
Анализируется экономическая целесообразность реализации проекта при следующих условиях величина инвестиции в инновацию - 10 млрд р , период реализации проекта 3 юда, доходы по годам (в млн р ) 400, 400, 500, текущий копффициент дисконтирования (без учета инфляции) 8%, среднегодовой ин­декс инфляции 6%

Если оценку делать без учета инфляции, то проект следует принять, по­скольку по формуле (9 6) NPV' = +1101,8 млн р

Анализ эффективности инновационных проектов в усло­виях риска основан на похожих идеях Поскольку основными характеристиками инвестиционного проекта в инновацию яв­ляются элементы денежного потока и ставка дисконтирова­ния, то учет фактора риска осуществляется поправкой одного из этих параметров.

Например, один из подходов связан с корректировкой де­нежного потока и последующим расчетом чистого приведен­ного эффекта (NPV) для всех вариантов (имитационное моде­лирование, или анализ чувствительности). Методика анализа в этом случае такова:

• по каждому проекту строят три его возможных варианта раз­вития: пессимистический, наиболее вероятный, оптимисти­ческий;

• по каждому из вариантов рассчитывается соответствующий чистый приведенный эффект, т.е. получают три величины: NPV_P,NPV_ml,NPV₀,

499

• для каждого проекта рассчитывается размах вариации NPV по формуле:

• из двух сравниваемых проектов тот считается более риско­ ванным, у которого размах вариации NPV больше.

Существуют модификации рассмотренной методики, пре­дусматривающие применение количественных вероятност­ных оценок. В этом случае методика имеет вид:

• по каждому варианту рассчитывается пессимистическая, наи­более вероятная и оптимистическая оценки денежных по­ступлений и чистый приведенный эффект {NPV);

• для каждого проекта значениям NPVp, NPV_ml, NPV_Q присваи­ваются вероятности их осуществления;

• для каждого проекта рассчитывается вероятное значение чистого приведенного эффекта, взвешенное по присвоенным вероятностям, и среднее квадратическое отклонение от него;

• проект с большим значением среднего квадратического от­клонения считается более рисковым.

Следует иметь в виду, что величина безрискового эквива­лента зависит от ряда факторов и может быть существенно ни­же исходной суммы дохода. Таким образом, не исключена ситу­ация, когда проект, приемлемый без учета фактора риска, стано­вится неприемлемым, если риск принимается во внимание.

Безрисковые эквиваленты можно находить разными спосо­бами. Например, можно попытаться оценить вероятность по­явления заданной величины денежного поступления для каж­дого года и каждого проекта. После этого составляются новые проекты на основе откорректированных с помощью понижаю­щих коэффициентов денежных потоков и для них рассчитыва­ются чистые приведенные эффекты (понижающий коэффици­ент представляет собой вероятность появления рассматривае­мого денежного поступления). По сути, откорректированный поток и представляет собой поток из безрисковых эквивален­тов. Предпочтение отдается проекту, откорректированный де­нежный поток которого имеет наибольший чистый приведен­ный эффект. Этот проект считается менее рисковым.

500

Следует иметь в виду, что в рассматриваемых подходах не учтены некоторые факторы, такие как налогообложение, воз­можное изменение цен на вновь приобретаемое оборудование, его производительность и др. В рамках ситуационного анализа учет этих факторов не представляет принципиальной трудно­сти. При этом все подобные расчеты весьма субъективны и многовариантны, а их результаты ни в коем случае не являют­ся единственным аргументом в пользу принятия того или ино­го решения.