АХД все / ЭММ и ЭВМ

Применение ЭВМ и ЭММ в анализе финансовых результатов

Финансовый анализ предприятия — это метод научного исследования и оценки явлений и процессов, в основе которого лежит изучение составных частей, элементов изучаемой организации. Он представляет собой оценку финансово-хозяйственной деятельности фирмы в прошлом, настоящем и предполагаемом будущем.

Автоматизация управления финансами дает руководителю мощный инструмент прогнозирования, выбора вариантов и анализа будущего финансового состояния предприятия, мониторинга его текущего состояния для принятия своевременных и адекватных управленческих решений [6].

В настоящее время существует огромное количество современных компьютерных программ и технологий, которые бы максимально облегчили проведение анализа финансовых результатов. Так, например, существуют компьютерные программы для автоматизации бухгалтерского учета: комплексная программа «Предприятие 1С», включающая в себя следующие аналитические блоки: «Бухгалтерия 1С», «Склад и торговля 1С», «Кадры 1С» и т. д. Данная программа позволяет сократить расходы времени бухгалтерии организации на ведение бухгалтерского учета и составления бухгалтерской отчетности.

В настоящее время существуют следующие программы:

1. Audit Expert позволяет быстро оценить финансовое состояние предприятия по его финансовой отчетности. На основании данных бухгалтерских отчетов можно получить аналитический баланс и отчет о прибылях и убытках, а также 20 основных финансовых показателей, характеризующих ликвидность, платежеспособность, рентабельность и деловую активность предприятия.

2. Пакет программ ЭКОНОМИЧЕСКИЙ АНАЛИЗ, предоставляя максимальные возможности, не требует настраивания предприятия под программу. Наоборот, в программе реализовано все, чтобы упростить процесс работы с пакетом. В программе реализован целый комплекс дополнительных особенностей, облегчающих и в то же время углубляющих и расширяющих финансово-экономический анализ, проводимый на предприятии [5].

3. ФинЭкАнализ 2016 ускоряет проведение финансово-экономического анализа организаций и делает его комплексным. Это незаменимый помощник для аудитора, экономиста, финансиста, бухгалтера и арбитражного управляющего.

4. Помимо описанных программных продуктов, существует порядка 200300 русифицированных программ оценки и анализа финансовых результатов организации, но далеко не все предприятия используют сегодня возможность оперативного управления своей финансовой деятельностью на базе программного компьютерного обеспечения.

Таким образом, использование информационных технологий при анализе финансового состояния предприятия позволяет значительно упростить ведение бухгалтерии и составление сводных отчетов, помогает выбрать оптимальные варианты решения конкретных задач, стоящих перед организацией, повышает эффективность работы организаций и способствует поддержанию финансовой стабильности предприятий [16].

Однако самым популярным для проведения анализа финансового состояния является Microsoft Excel, который дает пользователю целый инструментарий для анализа финансовой деятельности предприятия, проведения статистических расчетов и прогнозирования.

Так как данная программа является достаточно понятной и находится в свободном доступе, то для облегчения расчетов мы использовали выше в работе именно ее. Так, например, в таблице 2.1 - Состав и динамика финансовых результатов ОАО «Лидахлебопродукт» за 2019 – 2020 гг. мы рассчитывали изменение по сравнению с предыдущим годом и темп роста ,в таблице 3.2 – Расчет факторов изменения валовой прибыли на ОАО «Лидахлебопродукт» за 2019-2020 гг., в таблице 4.2 - Расчет факторов изменения прибыли от реализации продукции, товаров, работ, услуг на ОАО «Лидахлебопродукт», а также в таблице 5.2 - Расчет факторов изменения прибыли от текущей деятельности на ОАО «Лидахлебопродукт» мы облегчили расчет уровня влияния и структуры факторов. Также для облегчения работы мы провели вертикальный анализ в таблице 8.2 – Расчет факторов изменения прибыли до налогообложения на ОАО «Лидахлебопродукт», таблице 9.3 – Расчет факторов изменения чистой прибыли ОАО «Лидахлебопродукт» и в таблице 10.2 – Расчет факторов изменения совокупной прибыли ОАО «Лидахлебопродукт». Результаты проведенных работ можно увидеть в приложениях К, Л, Н, П, Р, Т, У. Для проведения данных расчетов мы также с помощью Excel составили таблицы, представленные в приложениях М, С, Л.

Для реализации статистических методов в программе Excel предусмотрен огромный набор средств. Часть из них – встроенные функции. Все формулы программы открыты и доступны для редактирования. Специализированные способы обработки данных доступны в надстройке «Пакет анализа».

Именно с использованием пакета анализа ниже нами будет произведен корреляционно-регрессионный анализ. Корреляционно-регрессионный анализ — это классический метод стохастического моделирования хозяйственной деятельности. Он изучает взаимосвязи показателей хозяйственной деятельности, когда зависимость между ними не является строго функциональной и искажена влиянием посторонних, случайных факторов. При проведении корреляционно-регрессионного анализа строят различные корреляционные и регрессионные модели хозяйственной деятельности.

Долю влияния учтенных факторов на результативный показатель мы будем рассматривать с помощью коэффициента детерминации (R²).

Корреляционно-регрессионный анализ мы будем проводить за период, равный 36 месяцам. В качестве результативного показателя является чистая прибыль (Y), в качестве факторов – уровень использования производственной мощности, % (фактор Х1) и выработка на одного работающего, тыс.руб. (фактор Х2). Для проведения анализа используем исходные данные, приведенные в таблице

12.1.

Таблица 12.1 – Исходные данные для проведения корреляционно-регрессионного анализа на ОАО «Лидахлебопродукт»

Наблюдение	Чистая прибыль, тыс.руб. (у)	Уровень использования производственной мощно- сти, % (х1)	Выработка на одного работающего, тыс.руб. (х2)
1	2	3	4
1	2,56	98,396	6,62
2	2	98,391	6,39
3	2,2	98,386	7,69
4	2,85	98,395	7,04
5	2,33	98,399	7,68
6	2,76	98,391	6,5
7	2,24	98,382	7,35
8	2,14	98,379	8,96
9	2,35	98,383	8,57
10	2,07	98,391	9,32
11	2,56	98,394	8,77
12	2,94	98,386	8,34
13	8,77	97,855	9,1
14	122,03	97,847	8,08
15	106,67	97,853	9,14
16	109,43	97,851	9,74
17	108,22	97,849	9,39
18	115,56	97,844	9,25
19	109,99	97,851	10,77
20	117,82	97,853	10
21	120,87	97,859	10,5
22	99,31	97,852	9,29
23	100,11	97,851	10,5
24	108,22	97,853	8,7
25	4,83	98,814	9,83
26	3,87	98,809	8,77
27	4,84	98,8	10,03
28	4,7	98,811	9,67
29	4,32	98,817	9,43
30	4,21	98,806	8,22
31	5,01	98,804	9,56
32	4,12	98,818	10,99
33	5,03	98,816	10,22
34	4,43	98,814	10,87
35	4,23	98,809	9,31
36	4,41	98,815	10,11

Примечание – Источник: собственная разработка на основании данных организации.

Результаты регрессионного анализа приведены ниже на рисунке 12.1

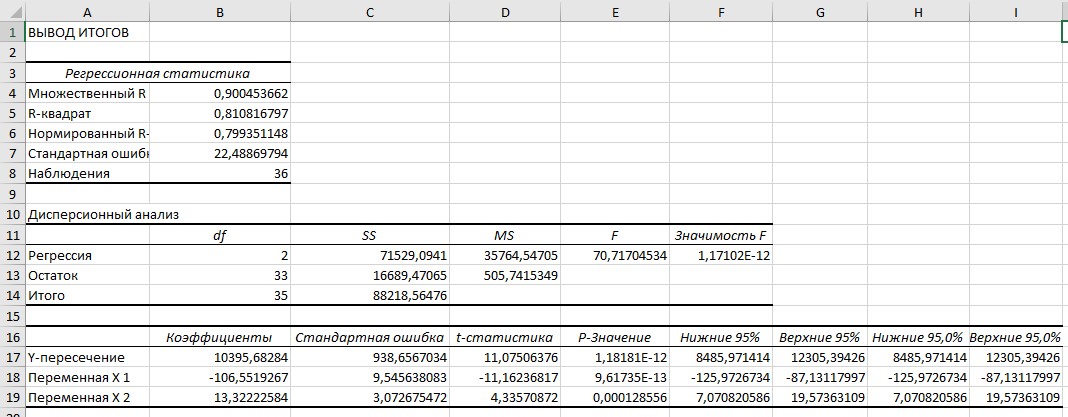
Рисунок 12.1- Результаты регрессионного анализа на ОАО «Лидахлебопродукт»

Примечание – Источник: собственная разработка.

После проведенного регрессионного анализа необходимо рассчитать коэффициенты парной корреляции для каждого фактора. Результаты мы видим на рисунке 12.2.

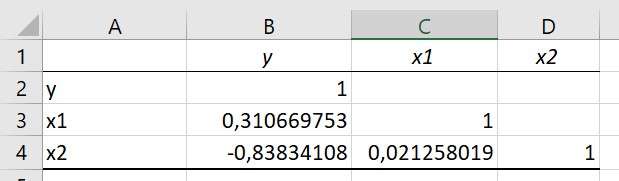
Рисунок 12.2- Матрица коэффициентов парной корреляции

Примечание – Источник: собственная разработка.

Факторы являются мультиколлинеарными, если коэффициент парной корреляции больше или равен 0,85. Существует формальное правило: любой фактор, включаемый в модель, должен влиять на результативный показатель сильнее, чем любые два фактора связаны между собой. Теперь проанализируем получившуюся матрицу.

Факторы х1 и х2 практически не связаны между собой (𝑟х1х2 = 0,02), что говорит об отсутствии мультиколлинеарности. Следовательно, оба фактора в модель будут включены.

Из матрицы коэффициентов видно, что на чистую прибыль оказывает сильное влияние выработка на одного работающего (ryx=0,84), уровень использования производственных мощностей оказывает слабое влияние на чистую прибыль (ryx=0,31).

Уравнение регрессии имеет следующий вид:

Y = 10395,7 - 106,55x1 + 13,32x2 (12.1)

Это уравнение показывает, что при увеличении уровня использования производственной мощности на 1%, чистая прибыль уменьшится на 106,55 тыс.руб, при увеличении выработки на одного работающего на 1 тыс.руб., чистая прибыль увеличится на 13,32 тыс.руб.

В корреляционной модели коэффициент множественной корреляции R= 0,90 свидетельствует о наличии сильной связи между выбранными факторами и результативным показателем. Коэффициент детерминации − одна из основных характеристик для измерения качества построенной регрессии, показывающая долю общего разброса относительно выборочного среднего − зависимой переменной, которая объясняется построенной регрессией. Чем выше коэффициент детерминации, тем лучше регрессия объясняет зависимость данных.

В нашем случае R² = 0,81 показывает, что изменение результативного признака на 81% обусловлено влиянием включенных в модель факторов, а 19 % составляет влияние неучтенных факторов, что является достаточно хорошим показателем.

Проверка значимости параметров множественного уравнения регрессии проводится с помощью расчета t-критерия Стьюдента. Ттабл.(n-m-1;α) = (33; 0,05) = 2,04. На основании данных рисунка 3 проведем проверку значимости выбранных факторов:

1. t₁ = 11,16>2,04 - коэффициент х1 статистически значим.

2. t₂ = 4,34>2,04 - коэффициент х2 статистически значим.

Проанализировав t- статистику, можно сказать, что наиболее влиятельным фактором на прибыль является уровень использования производственной мощности.

Для оценки значимости уравнения регрессии в целом предназначен критерий (F-статистика). Его пороговое значение является табличным и определяется на основе уровня надёжности, количества факторов в модели и количества наблюдений. F-статистика (критерий Фишера) используется для проверки гипотезы об отсутствии какой бы то ни было линейной зависимости между переменной и совокупностью факторов. Если наблюдаемое значение выше критического – уравнение регрессии значимо и может быть использовано в дальнейшем при прогнозировании. Табличное значение Fкр при степенях свободы k1 = 2 и k2 = 36-2-1 = 33 равно: Fкр (2;33) = 3,29. Поскольку фактическое значение F > Fкр (70,72 > 3,29), то коэффициент детерминации статистически значим и уравнение регрессии надежно.

Коэффициент вариации характеризует относительную меру отклонения измеренных значений от среднеарифметического:

, (12.2)

Где V – коэффициент вариации;

- среднеквадратическое отклонение; х - среднее арифметическое.

В статистике принято, что, если коэффициент вариации меньше 10%, то степень рассеивания данных считается незначительной, от 10% до 20% - средней, больше 20% и меньше или равно 33% - значительной, значение коэффициента вариации не превышает 33%, то совокупность считается однородной, если больше 33%, то – неоднородной.

Методику расчета коэффициента вариации для нашего примера можно увидеть на рисунке 12.3.

Рисунок 12.3- Расчет коэффициента вариации

Примечание – Источник: собственная разработка.

В нашем примере коэффициент вариации составил: - для фактора Y – 137,97%/ - для фактора Х1 – 0,40%.

- для фактора Х2 – 13,72%.

Таким образом, можно сделать вывод, что степень рассеивания для коэффициента Х1 является незначительной, для фактора Х2 – средней, а для фактора Y – весьма значительной.

Таблица 12.2- Исходные данные для проверки автокорреляции остатков

у	ух	еi	ei2	еi-еi-1	(еi-еi-1)2	(у-ух)/у
1	2	3	4	5	6	7
2,56	-0,2154	0,135891	0,018466	0	0	1,084141
2	-2,74625	0,226168	0,051152	0,135891	0,018466	2,373125
2,2	15,1025	-0,58218	0,338933	0,226168	0,051152	-5,86477
2,85	5,48555	-0,11194	0,012531	-0,58218	0,338933	-0,92475
2,33	13,58415	-0,50669	0,256737	-0,11194	0,012531	-4,83011
2,76	-1,28105	0,193862	0,037583	-0,50669	0,256737	1,464149
2,24	10,9999	-0,39244	0,154007	0,193862	0,037583	-3,91067
2,14	32,76475	-1,39389	1,942931	-0,39244	0,154007	-14,3106
2,35	27,14375	-1,12682	1,26973	-1,39389	1,942931	-10,5505
2,07	36,28135	-1,55817	2,427901	-1,12682	1,26973	-16,5272
2,56	28,6357	-1,18555	1,405525	-1,55817	2,427901	-10,1858
2,94	23,7605	-0,94485	0,892735	-1,18555	1,405525	-7,0818
8,77	90,46175	-3,73254	13,93182	-0,94485	0,892735	-9,31491

Окончание таблицы 12.2

1	2	3	4	5	6	7
122,03	77,72775	2,037392	4,150967	-3,73254	13,93182	0,363044
106,67	91,20765	0,716578	0,513484	2,037392	4,150967	0,144955
109,43	99,41275	0,467161	0,218239	0,716578	0,513484	0,09154
108,22	94,96385	0,61552	0,378865	0,467161	0,218239	0,122493
115,56	93,6318	1,012666	1,025492	0,61552	0,378865	0,189756
109,99	113,1324	-0,13558	0,018382	1,012666	1,025492	-0,02857
117,82	102,6629	0,702514	0,493525	-0,13558	0,018382	0,128647
120,87	108,6836	0,566422	0,320833	0,702514	0,493525	0,100823
99,31	93,3122	0,283139	0,080167	0,566422	0,320833	0,060395
100,11	109,536	-0,42331	0,179189	0,283139	0,080167	-0,09416
108,22	85,34685	1,055996	1,115127	-0,42331	0,179189	0,211358
4,83	-1,9961	0,3211	0,103105	1,055996	1,115127	1,413271
3,87	-15,5825	0,899429	0,808972	0,3211	0,103105	5,026499
4,84	2,1596	0,131228	0,017221	0,899429	0,808972	0,553802
4,7	-3,80765	0,398122	0,158501	0,131228	0,017221	1,810138
4,32	-7,64375	0,556417	0,3096	0,398122	0,158501	2,769387
4,21	-22,5889	1,235906	1,527465	0,556417	0,3096	6,365534
5,01	-4,527	0,445271	0,198266	1,235906	1,527465	1,903593
4,12	13,0289	-0,39959	0,159675	0,445271	0,198266	-2,16235
5,03	2,9856	0,102085	0,010421	-0,39959	0,159675	0,406441
4,43	11,8567	-0,33171	0,110028	0,102085	0,010421	-1,67646
4,23	-8,38975	0,586469	0,343946	-0,33171	0,110028	2,983392
4,41	1,62695	0,135922	0,018475	0,586469	0,343946	0,631077
Сумма			35		34,98	57,2652