2.5. Перспективный анализ прибыли

Перспективный анализ прибыли имеет целью выявление наиболее устойчивых закономерностей и тенденций в пред­шествующем периоде, прогнозирование на их основе показа­телей на перспективу, выбор альтернатив развития, выработку практических рекомендаций по определению наилучшего ва­рианта развития предприятия. Рассмотрим некоторые практи­ческие аспекты использования для перспективного анализа прибыли метода непосредственной экстраполяции корреля­ционно-регрессионного метода. Метод непосредственной экс­траполяции - наиболее простой способ прогноза. Его реко­мендуется использовать, если имеется однородная и обшир­ная по объему исходная информация, т.е. достаточно длинный временной ряд. Экстраполяция основана на изучении динами­ки изменения экономического явления (показателя) в пред-прогнозном периоде и перенесения выявленной закономер­ности на будущее. Достоинство метода состоит в его универ­сальности, а недостаток - в необходимости проведения боль­шого числа наблюдений, что ведет к снижению достоверности прогноза с увеличением срока его упреждения.

Динамический, или временной, ряд представляет собой со­вокупность числовых данных, характеризующих изменение показателя во времени. При построении временного ряда должна быть обеспечена сопоставимость отдельных его чле­нов. Для этого все элементы должны характеризовать изучае­мое явление за равные промежутки времени (для интерваль­ных рядов) или фиксировать его состояние в строго определен­ные моменты (для моментных рядов). Допускается построе­ние рядов с годовым исчислением признака с использованием более мелких единиц измерения времени: квартала, месяца, декады. Это дает возможность исследовать изменения показа­телей не только по годам, но и по кварталам, месяцам, декадам. Может возникнуть вопрос, какой длины брать ряд динамики для прогнозирования? Единого мнения по этому вопросу нет.

145

Одни авторы считают, что чем длиннее предпрогнозный пери­од (20-30 лет), тем достовернее выводы о перспективах изме­нения исследуемого явления в будущем. Другие считают, что для прогноза на будущее достаточно двух-трех лет, поскольку длинные ряды динамики преувеличивают роль прошлого в развитии исследуемого объекта. Третьи считают, что наилуч­шие результаты могут быть получены при использовании ря­дов динамики, содержащих не менее пяти и не более двадцати членов.

Экстраполирование найденной закономерности развития внутри динамического ряда за его пределы основано на инер­ционности экономических явлений. Наиболее простым мето­дом прогнозирования по одному ряду динамики является при­менение средних характеристик данного ряда: среднего абсо­лютного прироста и среднего темпа роста. Для первого случая расчетный уровень динамического ряда на любую дату y_t опре­деляется по формуле

Рассмотрим методику прогнозирования прибыли методом непосредственного экстраполирования с помощью среднего абсолютного прироста и среднего темпа роста. Исходная ин­формация представлена в табл. 2.9.

Средний абсолютный прирост по данным табл. 2.9 (гр. 3) равен:

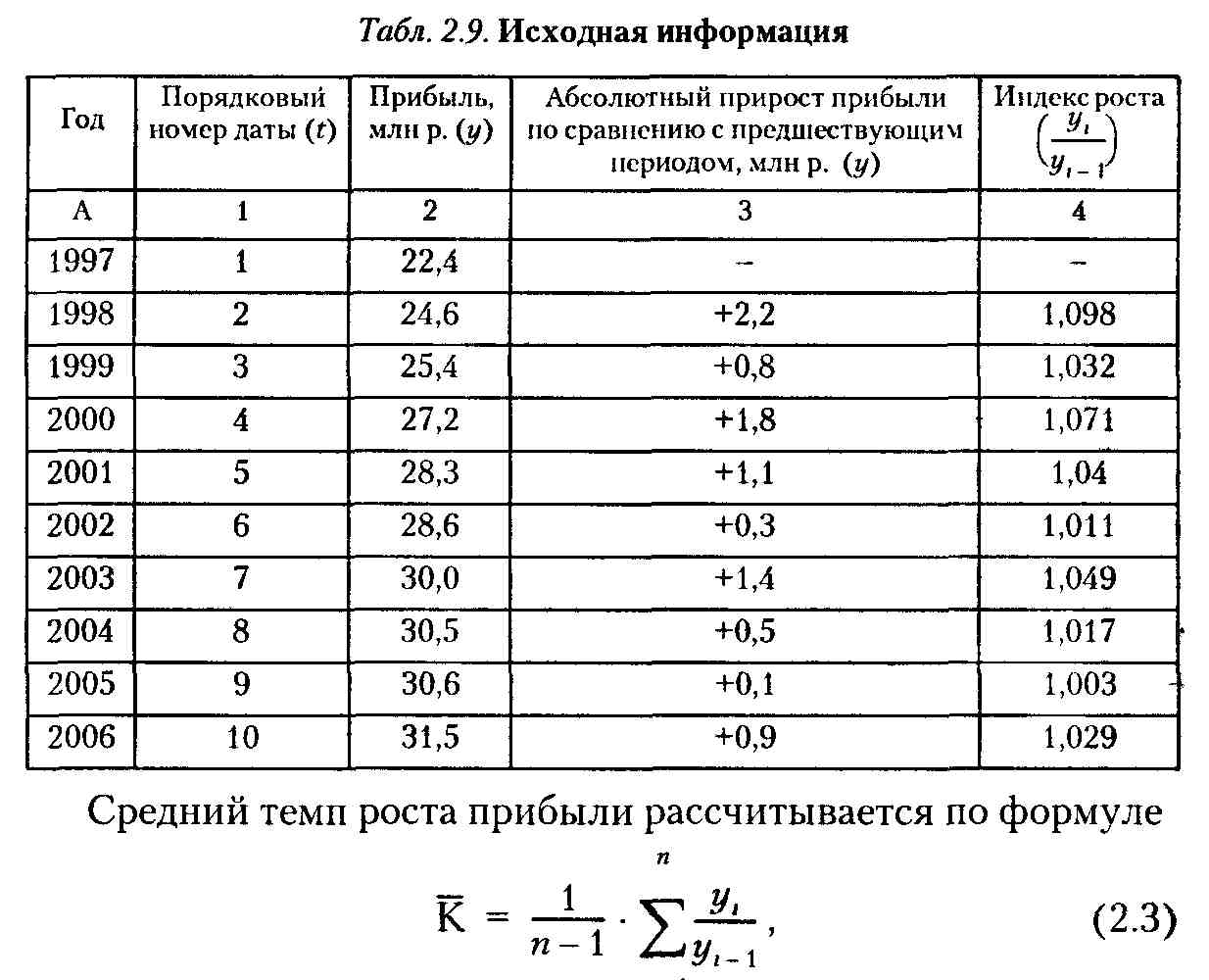
где п - число членов ряда.

По данным табл. 2.9, средний темп роста равен:

Прогноз прибыли в этом случае будет вестись по уравне­нию (см. формулу (2.2), табл. 2.9, гр. 2)

Используя полученные данные, рассчитаем прогнозные значения прибыли на 2007 г. Так, на базе среднего абсолютно­го прироста это составляет 32,5 млн р. [22,4 • 1,01 (11 - 1)],аис-ходя из среднего темпа роста - 32,8 млн р. [22,4 • 1,039^(11-1)].

Результаты прогноза, рассчитанные до 2016 г., обобщены в табл. 2.10.

Как показывают эти данные, уровень прогнозируемых зна­чений прибыли различен. Основная причина такого положе­ния заключается в том, что здесь не учитываются факторы формирования прибыли. Однако данная методика вполне приемлема для краткосрочного прогнозирования. Кроме того,

147

Табл 2 10 Расчетная таблица прогнозных значений прибыли, млн р.

Гол	Порядковый номер латы (0	Прогнозные значения прибыли (у,)
		по среднему абсолют­ному приросту	по среднему темпу роста
А	1	2	3
2007	11	32,5	32,8
2008	12	33,5	34,1
2009	13	34,5	35,4
2010	14	35,5	36,8
2011	15	36,5	38,3
2012	16	37,5	39,8
2013	17	38,6	41,3
2014	18	39,6	42,9
2015	19	40,6	44,6
2016	20	41,6	46,3

она может применяться для оценки качества краткосрочных прогнозов, полученных другими методами.

Прогнозирование прибыли по одному динамическому ряду имеет ограниченное применение для перспективного анализа, поскольку не дает представления о взаимосвязи прогнозируемо­го экономического явления с другими. Комплексный характер экономических явлений предполагает исследование не одиноч­ного динамического ряда, а параллельно нескольких рядов, коле­бания которых взаимообусловлены При этом возникает необхо­димость установления зависимости между такими колебаниями и измерения ее тесноты. Эти задачи решаются обычно с помощью корреляционно-регрессионного моделирования.

Корреляционная зависимость в отличие от функциональной является неполной, проявляется лишь в среднем и только в массе наблюдений. При корреляционной связи изменению аргумента соответствует несколько значений функций. В зависимости от количества отобранных факторов различают парные и много­факторные модели различного вида линейные, степенные, лога­рифмические В практике прогнозирования наибольшее распро­странение получили линейные модели вида

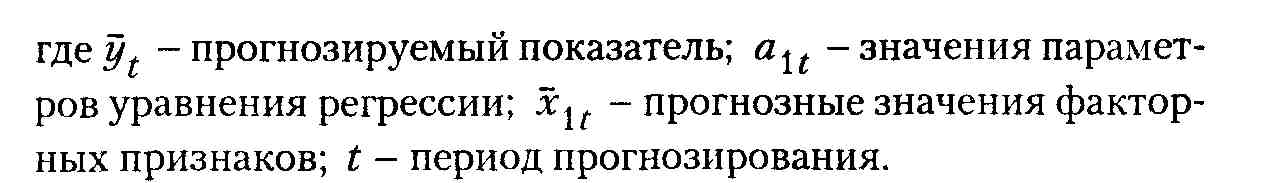
Предпочтение отдается линейным моделям по нескольким причинам: линейные модели просты, требуют меньшего числа вычислений; массовые экономические процессы, как правило, подчинены, закону нормального распределения, которому свойственны линейные формы связи.

Отбор факторов, включаемых в корреляционно-регрессион­ную модель, осуществляется в несколько приемов: логический отбор факторов в соответствии с их экономическим содержани­ем, отбор существенных факторов на основе оценки их значимос­ти по t-критерию Стьюдента, последовательный отсев незначи­мых факторов при построении регрессионной модели. -~ Упрощенно схема прогнозирования прибыли с использова­нием корреляционно-регрессионного анализа выглядит сле­дующим образом:

• исходная информация (табл. 2.11) обрабатывается на ЭВМ по типовой программе;

• полученное уравнение регрессии проверяется на значимость в общепринятом порядке;

• прогнозирование осуществляется по каждому одиночному динамическому ряду (фактору) методом непосредственной экстраполяции, в результате чего получаем прогнозные зна­чения каждого фактора на каждый год;

• подставляя полученные прогнозные значения (табл. 2.11, гр. 3, гр. 5) в уравнение регрессии, получаем прогнозные значения моделируемого показателя;

• точность прогноза проверяется путем сопоставления его ре­зультатов, полученных разными способами (табл. 2.11, гр. 1,2).

После обработки исходных данных на ЭВМ было получено следующее уравнение регрессии:

После статистического и экономического анализа парамет­ров уравнения произведен анализ соответствия фактических значений прибыли расчетным за анализируемый (предпро-гнозный) период (табл. 2.12).

149

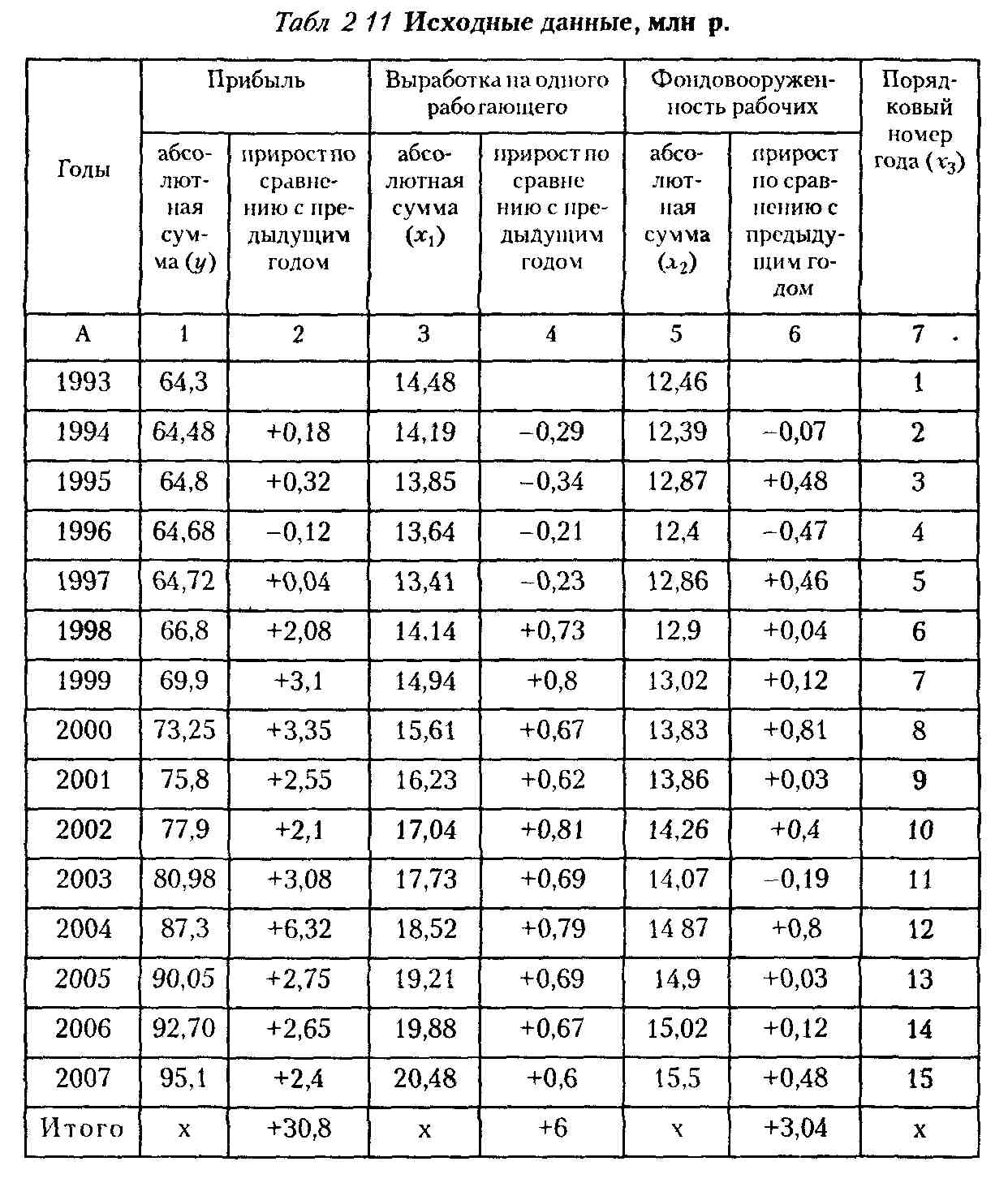
Как видим, отклонения незначительны, следовательно, можно использовать полученное уравнение регрессии для прогноза. Прежде чем приступить непосредственно к прогноз­ным расчетам прибыли, необходимо определить прогнозные значения каждого фактора каким-либо из способов по одиноч­ному динамическому ряду, например с использованием сред­них абсолютных приростов.

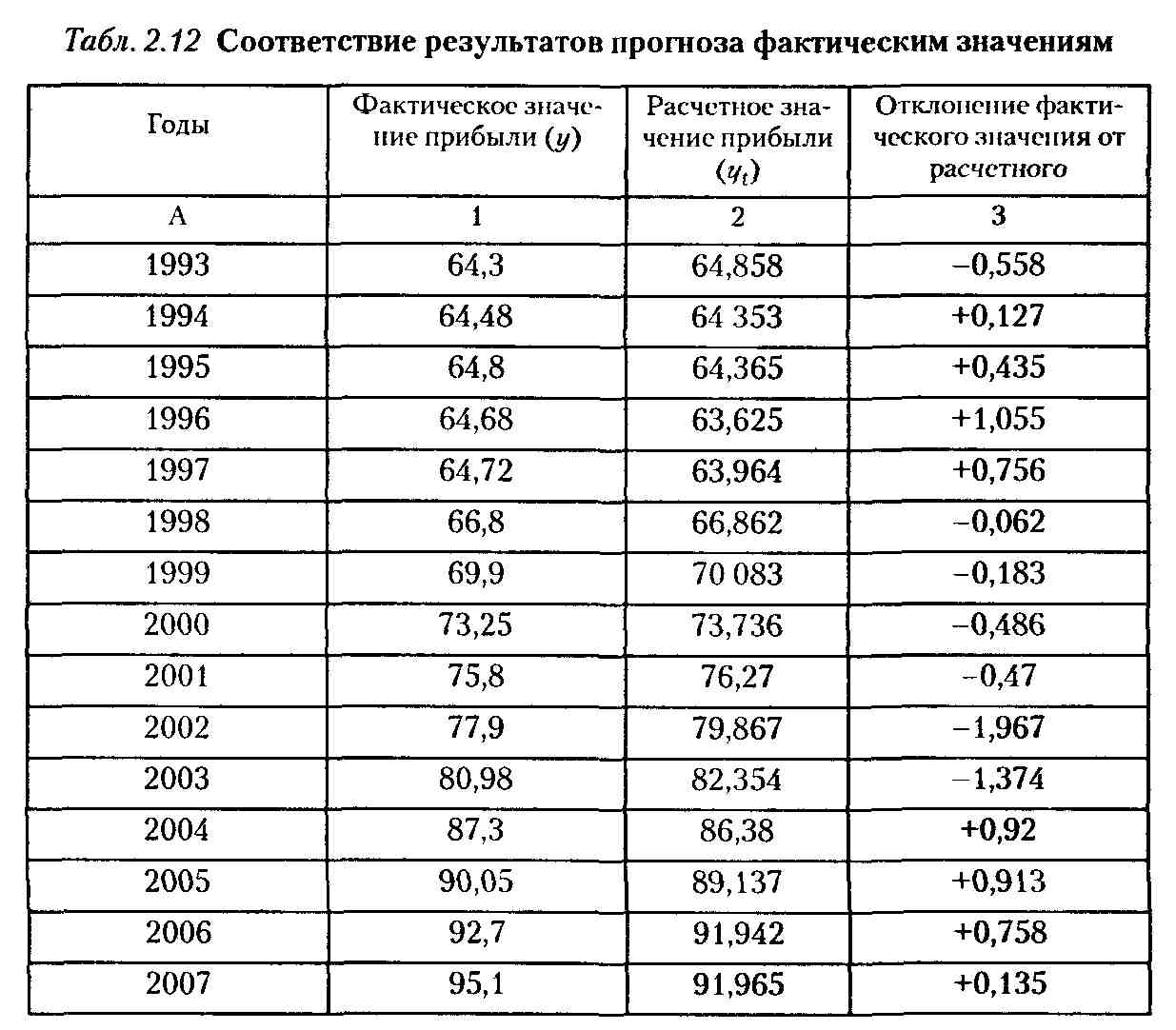
Для расчета по формуле (2.1) прежде всего необходимо опре­делить средний абсолютный прирост x_t и х₂ по данным табл. 2.12, что составляет по выработке на одного работающего 0,43 млн р.

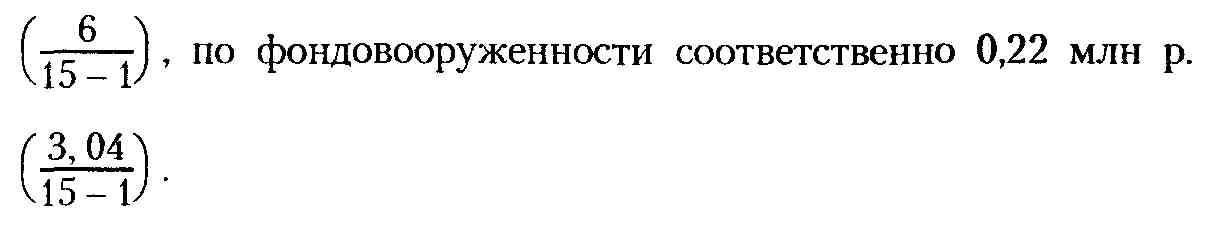
Подставляя эти величины в формулу (2.1), рассчитаем про­гнозные значения выработки и фондовооруженности на 2008-2013 гг. (табл. 2.11, гр. Зи 5) для дальнейшего использо­вания их при прогнозировании прибыли, например:

На базе этих показателей рассчитываются прогнозные зна­чения прибыли по полученному выше уравнению регрессии (табл 2 13, гр. 3, 5), например-

151

Для проверки точности найденных прогнозных значений прибыли сделаем расчеты этих показателей методом непо­средственной экстраполяции. Для этого воспользуемся форму-~ лой (2.1). Прежде всего определим средний прирост прибыли

Уравнение для расчета прогнозных значений прибыли при ис­пользовании абсолютного прироста имеет следующий вид:

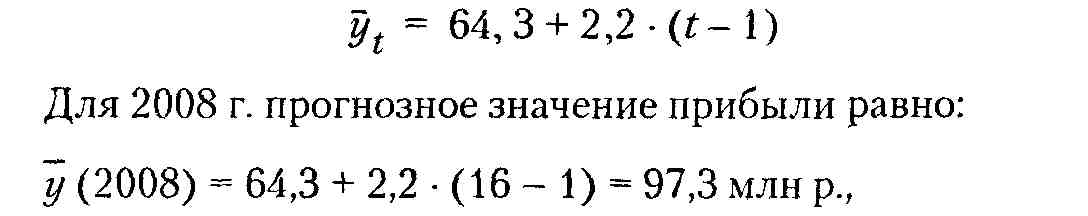
где 16 - порядковый номер года, следующего за 15-летним предпрогнозным периодом (см. табл. 2.13). Результаты расче­тов обобщены в табл. 2.13.

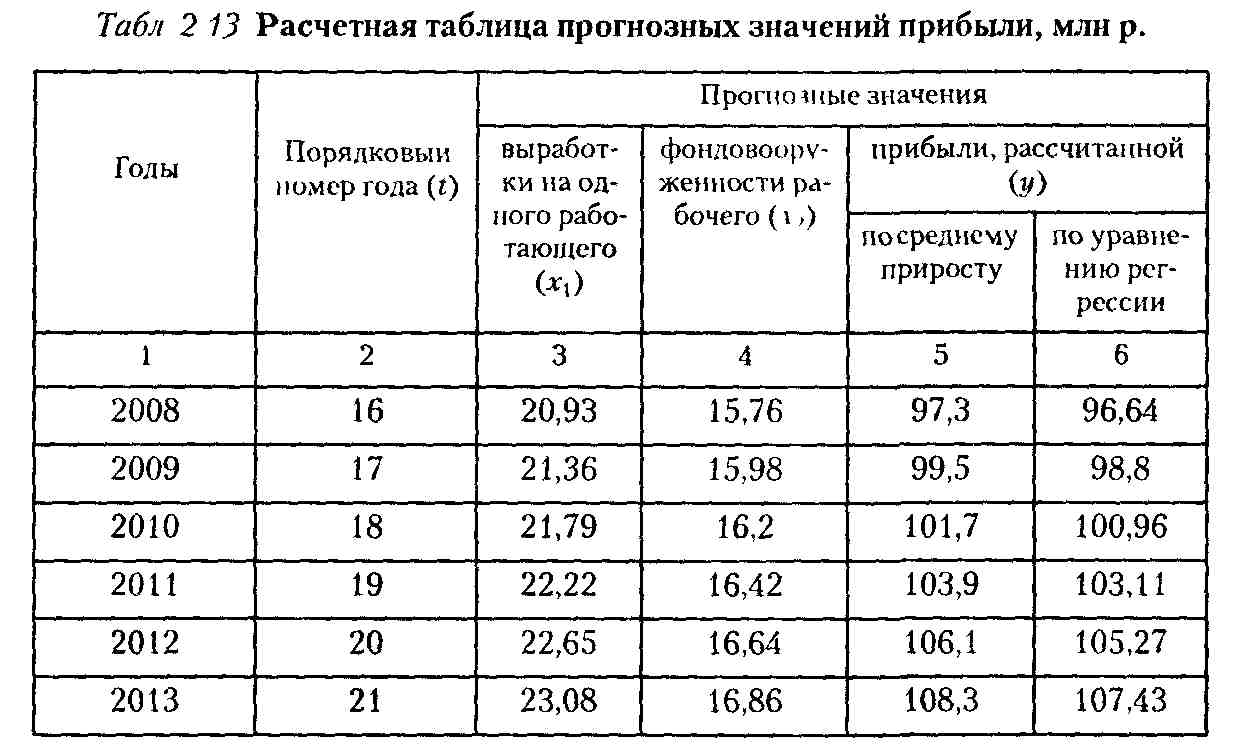
Анализ полученных результатов прогнозных значений прибыли показывает, что их уровень существенно не отлича­ется (см. табл. 2.13, гр. 5,6). Следовательно, прогноз достаточ­но надежен, его результаты могут использоваться для опреде-i ления перспектив развития.

152

Изложенные методы прогнозирования могут использоваться для прогноза объема продукции, производительности труда и других экономических показателей. Следует только вниматель­но и правильно подбирать соответствующие факторы.

Анализ полученных результатов показывает также, что бо­лее целесообразным является многофакторное прогнозирова­ние по нескольким рядам динамики, так как это позволяет учесть изменение во времени не только результативного пока­зателя, но и взаимосвязанных с ним факторов, а также обеспе­чивает большую точность прогноза.

Для перспективного анализа прибыли могут использовать­ся и другие методы прогнозирования.