23 Построение трендовой нелинейной модели: факторы, общий вид, оценка параметров, статистические характеристики

Факторы – t = 1, 2, 3, 4, … (время)

Общий вид:

1. Логарифмическая

2. Степенная

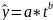
3. Параболическая

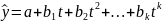
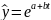
4. Экспоненциальная 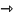ln y_t = a+bt

5. Гиперболическая 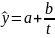y_t^-1

Оценка параметров: Метод наименьших квадратов (МНК) – метод оценивания параметров линейной регрессии, минимизир. сумму квадратов отклонений наблюдений завис. переменной от искомой линейной функции.

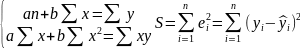
Статистические характеристики:

1) Коэффициент детерминации

Характеризует долю дисперсии результативного показателя y, объясняемую регрессией, в общей дисперсии результативного показателя.

2) F= , характеризует статистическую значимость уравнения

где m – число независимых факторов

то R² отличен от 0, уравнение значимо и переменные, вкл. в уравнение регрессии достаточно объясн. поведение зависимой переменной

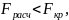то уравнение регрессии незначимо

3) ( ), S_a, S_b - стандартные ошибки коэффициента a и b

– коэффициенты статистически значимы

4) Тест Дарбина-Уотсона

DW=

24. Выделение сезонной компоненты: суть методики. Пример сезонной компоненты на квартальных данных, на недельных данных

модель аддитивная : Y = T+S+E.

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.

Выбор модели осуществляется на основе анализа структурных сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, выбирают аддитивную модель, в которой значения сезонной компоненты предполагаются постоянными для различных циклов.

Построение модели сводится к расчету значений T, S и E для каждого уровня ряда.

Процесс построение модели включает в себя следующие шаги:

1. Выравнивание исходного ряда методом скользящей средней.

2. Расчет значений компоненты S.

3. Установление сезонной компоненты из исходных уровней ряда и получение выравненных данных (T+E).

4. Аналитическое выравнивание уровней (T+E) и расчет значений T с использованием полученного уравнения тренда.

5. Расчет полученных по модели значений (T+S).

6. Расчет абсолютных и/или относительных ошибок.

Методика выделения сезонной компоненты, если она есть в структуре ряда:

1) Выравнивание ряда любым методом (метод скользящих средних; метод экспоненциального сглаживания; метод медианного сглаживания и др. Результатом процедуры сглаживания будет временной ряд выровненных значений 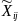не содержащих сезонной компоненты)

2) Для каждой переменной находим оценки сезонной компоненты

Аддитивная модель (если амплитуда сезонных колебаний не меняется во времени): , где T(t) – это трендовая компонента; S(t) – это сезонная компонента; ɛ(t)– случайный шум.

Мультипликативная модель (амплитуда сезонных колебаний изменяется во времени):

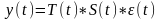
Если временной ряд представлен аддитивной моделью, то в качестве сезонной компоненты используется показатель абсолютного отклонения – Sai. ∑сезонных компонент (Sai) должна быть =0. Если мультипликативной – индекс сезонности (Isi). Произведение всех сезонных компонент, т. е. индексов сезонности Isi, должно быть =1.

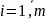Предположим, что задача состоит в исследовании временного ряда Xij, где i – это номер сезона (периода времени внутри года, например, месяца или квартала), , L – число сезонов в году, j – номер года, m – общее количество лет. Количество уровней исходного временного ряда равно n=L*m.