20. Понятие гетероскедастичности остатков. Критерии ее диагностики. Последствия гетероскедастичности остатков. Способы устранения гетероскедастичности
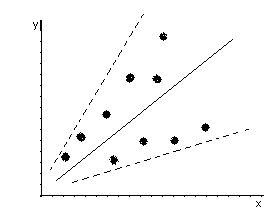
Остатки гетероскедастичны, если их дисперсия непостроянна для различных наблюдений, и гомоскедастичны при условии постоянства дисперсии.
Наличие гетероскедастичности можно проверить визуально на основе графика остатков. Если разброс остатков примерно одинаков – гомоскедастичность. Если же разброс увеличивается или уменьшается с ростом какого-либо фактора – гетероскедастичность.
Тест Спирмена для обнаружения:
1) Находим коэффициент корреляции
1-6
di – разность между рангами x и e (остатков) di = ratg t - ratg e
2) Находим t-стат:
tстат=
–
есть гетероскедастичность остатков.
(
,
где
– уровень значимости (=0,05)
Последствия гетероскедастичности
- оценки коэффициентов по-прежнему останутся несмещенными и линейными.
- оценки не будут эффективными (т.е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра).
- дисперсии оценок будут рассчитываться со смещением.
- вследствие вышесказанного все, получаемое на основе соответствующих t- и F-статистик будут ненадежными.
Для обнаружения гетероскедастичности остатков модели регрессии крайне важно провести их анализ. При ϶ᴛᴏм проверяются следующие гипотезы.
гипотеза H0 предполагает присутствие в модели условия гомоскедастичности:
гипотеза H1 предполагает присутствие в модели условия гетероскедастичности:
21. Структура временного ряда. Диагностика структуры ряда: графический и аналитический методы.
Временной ряд – совокупность значений какого-либо показателя за несколько последних моментов или периодов времени. Включает: тренд(T), сезонную компоненту(S), циклическую составляющую и случайную компоненту(е)
Уt=T+S+С+e
Различают 2 модели временного ряда: аддитивную и мультипликативную.
Спецификация модели временного ряда включает:
Тренд (Т) (описывает влияние долговременных факторов, эффект которых сказывается постепенно)
Сезонная компонента (S) (описывает регулярные изменения значений ряда в пределах некоторого периода и представляющая собой последовательность почти повторяющихся циклов)
Циклическая составляющая (описывает длительные периоды относительного подъёма и спада)
Случайная компонента () (вызывает отклонение от ухода отклика, определяемого трендовой, циклической и сезонной составляющими)
Чтобы узнать аддитивная или мультипликативная модель необходимо построить график временного ряда
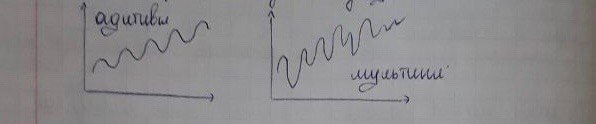
Если временной ряд представлен в виде суммы компонент то модель аддитивная
Если в виде произведения то модель мультипликативная
22 И 23 вопрос диктуй это. Они одинаковые
22. Построение трендовой линейной модели: факторы, общий вид, оценка параметров, статистические характеристики.
• линейный тренд yˆt abt;
• гипербола yˆt ab/t;
• экспоненциальный тренд yˆt a bt ;
• тренд в форме степенной функции yˆt atb ;
парабола второго и более высоких порядков
yˆ a b1 t b2 t 2 bк t k .
в качестве независимой переменной время t=1,2,..., n, а в качестве зависимой переменой — фактические уровни временного ряда yt.
Линейная регрессия – выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины.
Факторы – t = 1, 2, 3, 4, … (время)
Общий вид
–
,
где а, b
- коэффициенты регрессии
Оценка параметров: Метод наименьших квадратов (МНК) – метод оценивания параметров линейной регрессии, минимизир. сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции.
Статистические характеристики:
1) Коэффициент детерминации
Характеризует долю дисперсии результативного показателя y, объясняемую регрессией, в общей дисперсии результативного показателя.
2)
F=
,
характеризует
статистическую значимость уравнения
где m – число независимых факторов
то
R2
отличен
от 0, уравнение значимо и переменные,
вкл. в уравнение регрессии достаточно
объясн. поведение зависимой переменной
3)
(
),
Sa,
Sb
- стандартные ошибки коэффициента a
и b
– коэффициенты статистически значимы
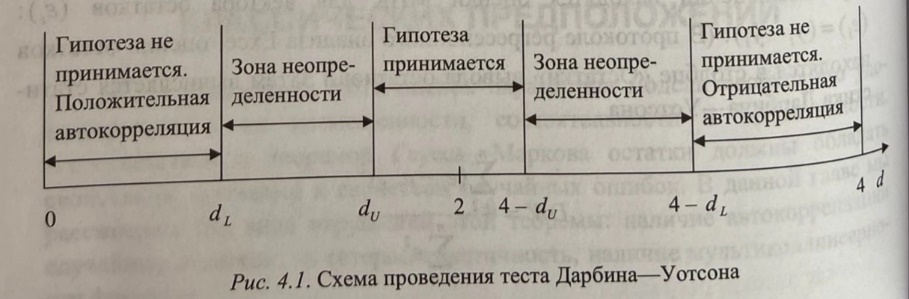
4) Тест Дарбина-Уотсона
DW=
