
- •Предмет и задачи эконометрики. Примеры экономических задач, решаемых с помощью аппарата эконометрики.
- •2.Стохастическая зависимость и функциональная зависимости. Диаграмма рассеяния и линия регрессии. Аналитическое описание линии регрессии.
- •Эконометрическая модель: экзогенные и эндогенные переменные модели, параметры модели. Информационная база для построения модели на пространственных данных и временных рядах.
- •Функция линейной регрессии
- •4.Парная линейная регрессия: аналитическое и графическое представление, остатки модели. Формирование поля входных показателей для построения модели с помощью надстройки «Анализ данных» в среде Excel.
- •5. Статистическое оценивание параметров парной линейной регрессии по методу наименьших квадратов.
- •6. Свойства мнк-оценок параметров парной линейной регрессии: теорема Гаусса-Маркова.
- •7. Проверка качества парной линейной регрессии: значимость параметров, адекватность модели.
- •8. Прогнозирование на основе парной линейной регрессии. Доверительный интервал прогноза. Экономическая интерпретация параметров модели
- •9.Парная нелинейная регрессия: аналитическое и графическое представление. Методика оценки параметров нелинейной регрессии. Свойства оценок.
- •10. Проверка качества парной нелинейной регрессии: значимость параметров, адекватность модели.
- •11. Прогнозирование на основе парной нелинейной регрессии: степенная, Экономическая интерпретация параметров парной регрессии в степенной форме связи.
- •12. Множественная линейная регрессия: аналитическое представление, остатки модели. Мнк-оценки параметров модели.
- •13.Свойства мнк-оценок множественной линейной регрессии. Теорема Гаусса-Маркова
- •14. Проверка качества множественной линейной регрессии: значимость параметров, адекватность модели.
- •15.Понятие мультиколлинеарности факторов. Последствия наличия, диагностика мультиколлинеарности, методы устранения.
- •16. Прогнозирование на основе линейной и нелинейной множественной регрессии. Экономическая интерпретация параметров регрессии.
- •17. Анализ зависимости между экономическими показателями на основе парной линейной регрессии.
- •18. Отличие методик построения регрессионной модели на временных рядах и пространственных данных: информационная база, набор статистических характеристик.
- •19. Понятие автокорреляции остатков модели. Критерии ее диагностики. Последствия автокорреляции остатков. Способы устранения автокорреляции.
- •20. Понятие гетероскедастичности остатков. Критерии ее диагностики. Последствия гетероскедастичности остатков. Способы устранения гетероскедастичности
- •Последствия гетероскедастичности
- •21. Структура временного ряда. Диагностика структуры ряда: графический и аналитический методы.
- •22 И 23 вопрос диктуй это. Они одинаковые
- •22. Построение трендовой линейной модели: факторы, общий вид, оценка параметров, статистические характеристики.
- •23 Построение трендовой нелинейной модели: факторы, общий вид, оценка параметров, статистические характеристики
- •24. Выделение сезонной компоненты: суть методики. Пример сезонной компоненты на квартальных данных, на недельных данных
- •25 И 26 вопросы диктуй вместе
- •25. Понятие стационарного и нестационарного временного ряда: графическое представление. Приведение нестационарного временного ряда к стационарному виду.
- •25 И 26 вопросы диктуй вместе
- •26. Методика построения эконометрической модели на нестационарных временных рядах.
- •27. Понятие авторегрессионной модели: общий вид модели, набор статистических характеристик.
- •28. Понятие эконометрической модели с распределенными лагами. Экономическая постановка задачи. Общий вид модели, набор статистических характеристик.
- •229.Отчетный моб как информационная база моделей прогнозирования отраслевых показателей промышленности: материально-вещественная структура моб
- •330. Отчетный моб как информационная база моделей прогнозирования отраслевых показателей промышленности: финансовая структура моб
- •Коэффициенты прямых затрат: определение, экономический смысл, методика расчета
- •32. Модель прогнозирования ценовых пропорций отраслей промышленности в условиях роста цен на ресурсы
- •33. Модель прогнозирования ценовых пропорций отраслей промышленности в условиях роста заработной платы
- •34. Модель прогнозирования ценовых пропорций отраслей промышленности в условиях роста ставки косвенных налогов
- •35. Модель прогнозирования объема и структуры валового выпуска промышленности в зависимости от конечного спроса на продукцию отраслей
- •36. Модель прогнозирования ввп в зависимости от объема производства в отраслях промышленности
- •Постановка задачи управления комплексом взаимосвязанных работ в контексте сетевого планирования.
- •38. Входные данные для построения сетевой модели.
- •39. Основные определения и показатели сетевого планирования и управления. Основные принципы построения сетевого графика.
- •40. Основные показатели сетевого планирования: сроки свершения событий, резервы события, время начала работы, время окончания работы.
- •41. Основные показатели сетевой модели: критические работы, критические события, критический срок, их интерпретация..
- •42. Календарный график работ (график Ганта): общий вид в контексте сетевой модели, его интерпретация
- •43. Построение графика потребности в ресурсах: концепция расчета в контексте сетевой модели, его интерпретация.
- •44. Модели управления запасами как инструмент закупочной логистики: постановка задачи.
- •45 Понятие экономичного объема заказа: определение, графическое представление.
- •46 Понятие точки заказа: определение, графическое представление, формула расчета
- •47.Зависимость затрат запасообразования от размера поставки: графики, аналитические зависимости.
- •48. 48. Формула Уилсона для расчета экономичного объема заказа.
- •49. Допущения формулы Уилсона
- •50. Расчет оптимальных параметров управления запасами.
- •51. Модели теории игр как инструмент выбора оптимальной стратегии: постановка задачи.
- •52. Основные понятия и определения статистических игр: состояние природы, стратегии, платежная матрица, ее экономический смысл.
- •53. Характ-ка условий неопределенности. Критерии принятия решений в условиях неопределенности.
- •54 .Характеристика условий риска. Критерии принятия решений в условиях риска.
- •55 .Модель формирования оптимальной инвестиционной программы при ограничениях бюджета
- •56.Модель оптимизации производственной программы предприятия и ее модификации
- •57. Оптимизационная модель задачи развития и размещения производства
- •58. Модель оптимизации технологических процессов в промышленности
54 .Характеристика условий риска. Критерии принятия решений в условиях риска.
При выборе наилучших стратегий различают: ситуацию, где вероятности состояний природы неизвестны,т е принятие решений в условиях неопределенности, и ситуацию, где вероятности состояний природы известны, т е принятии решений в условиях риска.
Критерий выбора наилучших решений в условиях риска
Для принятия
решений в условиях риска используется
критерий
Байеса. Пусть
принимающий решение имеет m
стратегий, а природа n,
причем состояние природы Пj
реализуется с вероятностью рj,
для
каждой стратегии Ai
рассчитывается ожидаемый выигрыш
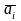 ,
,

Наилучший по Байесу будет стратегия Аi, соответствующая наибольшему ожидаемому выигрышу

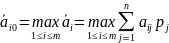
,
55 .Модель формирования оптимальной инвестиционной программы при ограничениях бюджета
Чистая текущая ценность –
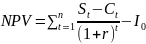 ,
где St
– поступления в году t,
Ct
– затраты в году t,
r
– ставка дисконта;
,
где St
– поступления в году t,
Ct
– затраты в году t,
r
– ставка дисконта;Внутренняя норма прибыли –
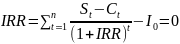 ,
проект считается привлекательным, если
IRR
превышает ставку дисконта;
,
проект считается привлекательным, если
IRR
превышает ставку дисконта;Период окупаемости –
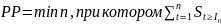
Индекс прибыльности – PI (чем больше значение этого показателя, тем выше отдача каждого рубля)
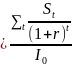 ,
где I0
– начальные инвестиции.
,
где I0
– начальные инвестиции.
Оптимизация инвестиционной программы может быть пространственной и временной: 1) Временная оптимизация может проводиться, если: общая сумма финансовых ресурсов, доступных в планируемом году, ограничена сверху; имеется несколько независимых инвестиционных проектов, которые из-за ограниченности финансовых ресурсов не могут быть реализованы в планируемом году одновременно, однако в году, следующем за планируемым, оставшиеся проекты либо их части могут быть реализованы; требуется оптимальным образом распределить проекты по двум годам. 2) Пространственная оптимизация проводится, если: общая сумма финансовых ресурсов на конкретный период (например, год) ограничена сверху; имеется несколько независимых проектов с суммарным объемом требуемых инвестиций, превышающим имеющиеся у предприятия ресурсы; требуется составить инвестиционную программу, максимизирующую суммарный возможный прирост капитала.
56.Модель оптимизации производственной программы предприятия и ее модификации
Задача формулируется
следующим образом. Предприятие выпускает
несколько
видов продукции
,
обладая ограниченными запасами ресурсов
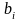 . Известны нормы затрат ресурса i
на производство единицы продукции j
aij.
Требуется найти структуру производства
продукции, на которой обеспечивается
максимум эффекта от выпуска (максимум
выручки от реализации, минимум затрат).
Если pj
обозначить эффективность единицы
продукции j
(например, цена), то модель в общем виде
запишется:
. Известны нормы затрат ресурса i
на производство единицы продукции j
aij.
Требуется найти структуру производства
продукции, на которой обеспечивается
максимум эффекта от выпуска (максимум
выручки от реализации, минимум затрат).
Если pj
обозначить эффективность единицы
продукции j
(например, цена), то модель в общем виде
запишется:
максимизируется выручка от реализации
 (1)
(1)
при ограничениях на запас i -го ресурса
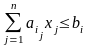 ,
(2)
,
(2)
и неотрицательности переменных

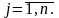 (3)
(3)
Если существует
ограничение на спрос продукции j-го
вида (dj),
то модель модифицируется: в модель
дополнительно вводится ограничение
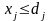 .
.
Заметим, что модель (1)-(3) может быть не только на максимум выручки, но и на минимум затрат. Пусть cj -затраты энергоресурсов на выпуск единицы продукции j -го вида. Тогда критерий оптимальности:
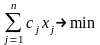
при неизменных ограничениях (2)-( 3).
Чтобы значение
критерия оптимальности не скатывалось
до 0, решение необходимо ограничить
снизу, например, ввести ограничения на
выполнение госзаказа ( ).
Решение задачи на минимум затрат имеет
смысл, если ввести ограничения на объемы
производства с меньшей степенью
подробности. Например, должен быть
выполнен целевой показатель по валовому
выпуску продукции в целом (P):
).
Решение задачи на минимум затрат имеет
смысл, если ввести ограничения на объемы
производства с меньшей степенью
подробности. Например, должен быть
выполнен целевой показатель по валовому
выпуску продукции в целом (P):
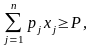
где pj — цена единицы продукции j-го вида.
Если в систему вводят ограничение использования ресурса:
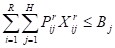 где
Prij -расход
ресурса J-го
вида I-й
продукции при изготовлении r-м
способом (1…R,
1…H);
Bj-
лимит получения j-того
вида ресурса.
где
Prij -расход
ресурса J-го
вида I-й
продукции при изготовлении r-м
способом (1…R,
1…H);
Bj-
лимит получения j-того
вида ресурса.
