52. Основные понятия и определения статистических игр: состояние природы, стратегии, платежная матрица, ее экономический смысл.

Игра - это модель конфликтной ситуации.

Игроки - конфликтные стороны.

Стратегии - возможные действия игроков.

Оптимальная стратегия - приносит игроку максимальный средний выигрыш, или минимальный средний проигрыш.

Статистическая игра – игра, в которой один из игроков – природа (не сознательно действующий).

Цель статистических игр – выбор оптимальной стратегии.

Пусть у игрока, действующего сознательно, есть m стратегий: А₁, А₂, … А_m, а у второго игрока – природы есть n стратегий: П₁, П₂, …, П_m. Прибыль или убыток сознательного игрока обозначим а_ij; Тогда можно построить таблицу, которая называется платежной матрицей, обозначим ее А:

П₁ П₂ … П_n

А₁ а₁₁ а₁₂ … а_1n

А=

А₂ а₂₁ а₂₂ … а_2n

… … … … …

А_m а_m1 а_m2 … а_mn

Где А – строки, кот соответствуют стратегиям игрока, а столбцы – стратегии игрока В. Целью игроков явл выбор наиболее выгодных стратегий, доставляющих игроку А max выигрыш, а игроку В – min проигрыш.

53. Характ-ка условий неопределенности. Критерии принятия решений в условиях неопределенности.

Цель статистических игр – выбор наилучших стратегий.

Пусть у игрока, действующего сознательно, есть m стратегий (А₁, А₂, … А_m), а у второго игрока – природы есть n стратегий ( П₁, П₂, …, П_m). Выигрыш или проигрыш сознательного игрока, в случае, если он выберет стратегию А_i, а природа реализует стратегию П_j, обозначим а_ij; . Тогда строим таблицу: A платежная матрица,:

П₁ П₂ … П_n

А₁ а₁₁ а₁₂ … а_1n

А=

А₂ а₂₁ а₂₂ … а_2n

… … … … …

А_m а_m1 а_m2 … а_mn

При выборе наилучших стратегий различают: ситуацию, где вероятности состояний природы неизвестны,т е принятие решений в условиях неопределенности, и ситуацию, где вероятности состояний природы известны, т е принятии решений в условиях риска.

Критерии выбора наилучших стратегий в условиях неопределенности.

1. Критерий Вальда. принимающий решение для каждой стратегии А_i находит наименьший выигрыш а_i=min а_ij, . Затем среди наименьших выигрышей он находит наибольший:

(6.4.1)

Стратегия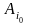 , соответствующая 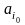будет наилучшей по Вальду. Ее часто называют максиминной стратегией.

2. Критерий Сэвиджа. Риском r_ij, 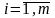, , принимающего решение называют разницу между тем выигрышем, который он бы получил, если бы знал, какое состояние реализует природа и его реальным выигрышем, то есть, r_ij=β_ij – , где .

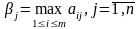П₁ П₂ … П_n

А₁ r₁₁ r₁₂ … r_1n

Матрица рисков R имеет вид:

А₂ r₂₁ r₂₂ … r_2n

R=

… … … … …

А_m r_m1 r_m2 … r_mn

Принимающий решение для каждой стратегии А_i находит максимальный риск r_i, r_i= . Затем из максимальных рисков выбирает минимальный:

(6.4.2)

Стратегия А_i0, соответствующая минимальному из максимальных рисков r_i0, будет наилучшей по Сэвиджу.

3. Критерий Гурвица. Критерий Гурвица является критерием пессимизма-оптимизма. Наилучшей по Гурвицу является стратегия А_i0, соответствующая числу а_i0, которое рассчитывается по формуле:

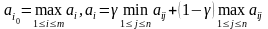(6.4.3)

Значение параметра γ задает принимающий решение на основании своего опыта и характера. Если γ=1, то критерий Гурвица преобразуется в критерий крайнего пессимизма:

.

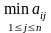Если γ=0, то получаем критерий крайнего оптимизма:

.

Обычно, на практике, выбирают 0<γ<1.