эконометрика / эконометрика / задачи

1. общий вид регрессионной модели

yˆ  a  b  x (yˆ- игрик с крышечкой)

где

У-зависимый показатель, результ пока-ль,

Х-независимый пока-ль, фактор

А,в –параметры, коэф-ты модели

2. построить календарный график

Рисуем график

Горизонтальная ось t–отмечаем отрезки времени, например от 1-12

Вертикальная ось (i,j) – отмечаем работы, например (1,2); (1,3) и тд

Если работы выполняются одновременно то на горизонтали они начинаются с одного момента времени

3. построить сетевой график

Кружок делиться на 4 секции:

В верхней – номер события

В нижней – резерв

В левой-ранний срок t_р

В правой- поздний срок t_п

Сразу находим ранний срок совершения события. Для этого из события 1 двигаемся в порядке возрастания номеров. T_p (1)=0 , 0 записываем в левый сектор кружка. T_p (2)= T_p (1) + время на совершение этого события и тд. Если в событие входит 2 работы то выбираем максимальное время. В конце вычислений находим ранний срок последнего собития и это будет t_кр

Находим поздний срок совершения события. Для этого из последнего события в порядке убывания к первому событию. Записываем в правый сектор кружка. Для этого правый кружок – время на выполнение

Далее вычисляем резервы времени. Записываем в нижнюю жасть кружка. Нужно правую часть кружка-левая часть кружка

Далее выделяем критический путь – резервов нет. Допустим L_кр(1-2-3-4-5)

Далее находим ранний срок начала работы

Ранний срок окончания работы

Поздний срок начала работы

Поздний срок окончания работы

4. про сезонную компоненту

Сезонная компонента (S) (описывает регулярные изменения значений ряда в пределах некоторого периода и представляющая собой последовательность почти повторяющихся циклов)

Аддитивная модель – одинаковые отреезки времени

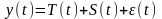
Мультипликативная –отрезки времени изменяются

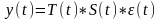
5. Критерий Байеса

Если игроку A заранее известны вероятности pj состояний природы, то оптимальную стратегию можно найти при помощи расчета средних выигрышей для каждой стратегии:

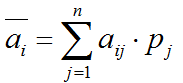
Для этого мы находим среднее значение по каждой строчке

Оптимальной по критерию Байеса будет считаться стратегия, которой соответствует максимальный средний выигрыш:

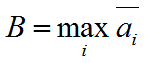
6. Критерий Вальда

Это критерий крайнего пессимизма или крайней осторожности. Оптимальной считается та стратегия, которой соответствует максимальный из минимальных (гарантированных) выигрышей: ( выбираем статегию с минимальным средним выигрышем )

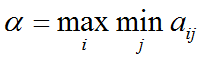
7. Критерий Гурвица

Это критерий оптимизма-пессимизма. Для каждой стратегии считают средний выигрыш, как среднее взвешенное между максимальным и минимальным выигрышем:

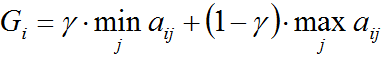
Оптимальной по критерю Гурвица считается стратегия, которая приносит игроку максимальный средний выигрыш:

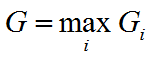
8. Критерий Сэвиджа

Это критерий минимаксного риска. На основе платежной матрицу рассчитывают элементы матрицы рисков по формуле:

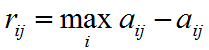
1. в каждой строке выбираем максимальное значение

2. в каждом столбце отнимает от максимального все остальные и записываем в матрицу R=

3. в полученной матрице в каждой строке выбираем мах значение

4. из выбранных мах значений выбираем минимальное

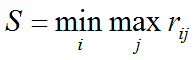
Это значение соответствует оптимальной стратегии 1-го игрока по критерию Сэвиджа. Т.е. определяется стратегия, которая принесет потери не более S единиц.

9. На основе таблицы записать регрессивную модель

Для начала составим таблицу где найдем х², у², х*у, а так же сумму по каждому столбцу

Запишем систему уравнений

a*n( где n- количество строк, наблюдений) + сумма по столбцу х*b=сумма по столбцу у

сумма по столбцу х*a+сумма по столбцу х²*b=сумма по столбцу x*y

все это под знаком системы

решим эту систему и получим коэффициент b

теперь найдем коэффициент а из любого уравнения системы

получим коэффициенты регрессии и запишим уравнение у с крышечкой=ах+b

характеристика: уравнение регрессии задает зависимость среднего значения случайной переменной у от значений х

при увеличении показателя х на 1 еденицу показатель у с крышечкой увеличится на а

Рассчитаем параметры степенной функции

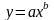
Данную функцию можно привести к линейному виду путем логарифмирования обеих частей:

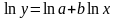
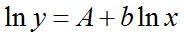
Потенцирование

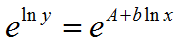
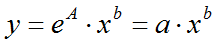
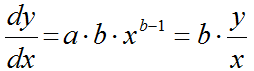
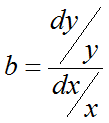
коэффициент b в степенной модели показывает относительное изменение фактора y при увеличении значения фактора x на 1%. Т.е. имеет смысл коэффициента эластичности.

10. интервальный прогноз

в уравнение подставляем число вместо х. все это будет у_пр

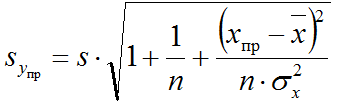
s – стандартная ошибка

n – количество наблюденй

х с черночкой – среднее значение х

х_пр – число на которое мы умножали х

дисперсия х

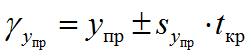
11. точечный прогноз

Точечным прогнозом для у_р является 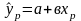, т.е. чтобы получить точечный прогноз нужно в построенное уравнение регрессии подставить заданное значение независимой переменной.

12. Оптимальный объем запаса

Экономичный размер заказа (EOQ) определяется по формуле Уилсона, имеющая вид:

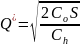- формула Уилсона

(аналитическая ф-ла для расчета эконом. объема заказа (оптим. размера))

где S – спрос

Co – затраты на выполнение одного заказа, д.е.

Ch – затраты на содержание единицы запаса в течение периода Т, д.е.

13. Управление запасами

оптимальный размер партии поставки

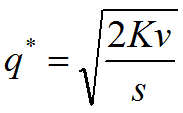
К – издержки размещения

V – штуки

s- за 1 штуку

Оптимальный интервал между поставками:

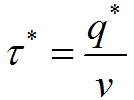
Годовые издержки

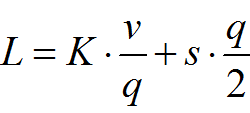
Точка заказа

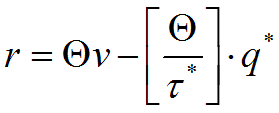
Где кружочек непонятный – время выполнения заказа

минимальный начальный запас I₀ , равный:

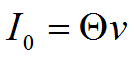
14. Найти остатки

Берем х по номером 2 и вставляем в уравнение получится у с крышечкой.

Берем у под номером 2 и вставляем в уравнение получится у

Остатки = у-у с крышечкой

15. определить какие факторы статистически значимые

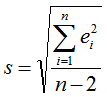
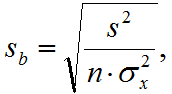
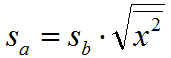
Коэффициент детерминации 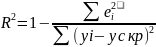оценивает качество модели.Находится в промежутке от

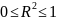
Если 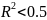, то качество уравнения плохое

Если 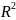находится между 0,5 и 0,8 –удовлетворительное

Если находится между 0,8 и 0,9 -хорошее

Если находится между 0,9 и 0,99 -высокое

Если находится между 0,99 и 1 -очень высокое качество.

Статистики Стьюдента параметров оцениваю их статистическую значимость. Если t>tкр, то коэффициенты статистически значимы.

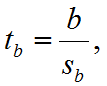
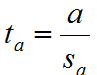
16. Составить отчетный моб

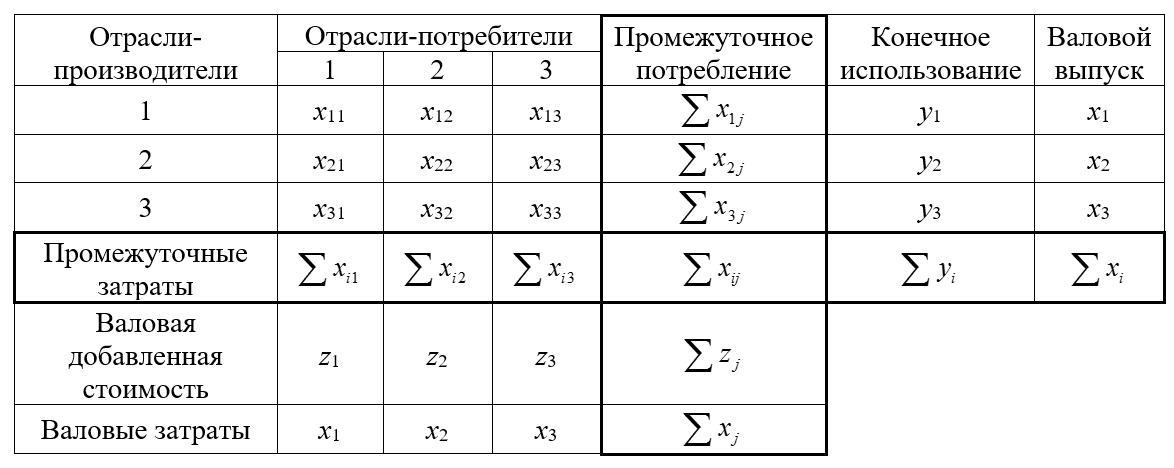
Матрицу х вставляем

Вектор конечного использования это у

Промежуточные затраты эо сумма столбца 1 ;2;3 и тд

Промежуточное потребление это сумма строк

Валовый выпуск равен валовым затратам и равен промежуточное потребление +конечное использование

Валовая добавленная стоимость равна валовые зараты – промежуточные затраты

Чтобы найти плановый моб нужно найти новые а

Для этого нужно х₁₁ разделить на валовые затраты и тд

Составим матрицу А с новыми значениями

Если дано Хплан то считаем у

Х1=а11х1+а12х2+у1

Х2=а21х1+а22х2+у2 все это под знаком системы

Составляем новую таблицу планового моба

Пересчитываем все показатели

17. наличие тенденции методом скользящей средней

Сумма у разделить на их количество

18 Модель сезонных колебаний

Аддитивная модель (если амплитуда сезонных колебаний не меняется во времени): , где T(t) – это трендовая компонента; S(t) – это сезонная компонента; ɛ(t)– случайный шум.

Мультипликативная модель (амплитуда сезонных колебаний изменяется во времени):

Если временной ряд представлен аддитивной моделью, то в качестве сезонной компоненты используется показатель абсолютного отклонения – Sai. ∑сезонных компонент (Sai) должна быть =0. Если мультипликативной – индекс сезонности (Isi). Произведение всех сезонных компонент, т. е. индексов сезонности Isi, должно быть =1.

Предположим, что задача состоит в исследовании временного ряда Xij, где i – это номер сезона (периода времени внутри года, например, месяца или квартала), 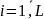, L – число сезонов в году, j – номер года, 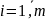m – общее количество лет. Количество уровней исходного временного ряда равно n=L*m.

19 что то про лаги

Общий вид:

y_t = a + b₁x_t + b₂x_t-1 + ε_t – модель распред. лагов DL (1) (в скобках максимальный лаг)

y_t = a + b₁x_t-1 + b₂x_t-1 + ε_t – авторегресс. модель распред. лагов ADL (1, 1) (макс. лаг экзо- и эндогенных переменных)

Стат. характеристики:

Ориентир. на t -ст:

y_t = a + bx_t-1

Лаг S определяется по R² и t -ст.

1)

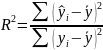
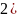
1-6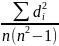

d_i – разность между рангами x и e (остатков)

2) Находим t-стат:

t_стат=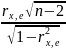

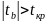– есть гетероскедастичность остатков.

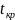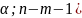( , где 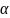– уровень значимости (=0,05)

Если t -ст указывает на незначимость – исключаем этот регрессор.

В этом случае автокорреляцию остатков оцениваем с помощью h-статистики Дарбина:

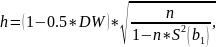
где 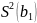– квадрат стандартной ошибки коэфф. Регрессии при лаговой зависимости.

Если выборка большая, автокорреляция остатком м.б. отклонена при |h|>1,96.