25. Понятие стационарного и нестационарного временного ряда: графическое представление. Приведение нестационарного временного ряда к стационарному виду.

Стационарные ряды – временные ряды, у которых среднее значение и дисперсия постоянны, временные показатели имеют одинаковую степень связи, ковариации между значениями c лагом зависят только от величины лага и не зависят от времени.

Пример стацион. временного ряда – белый шум: среднее и ковариации равны нулю, дисперсия постоянна, корреляция = 0, то есть нет лин. завис-ти.

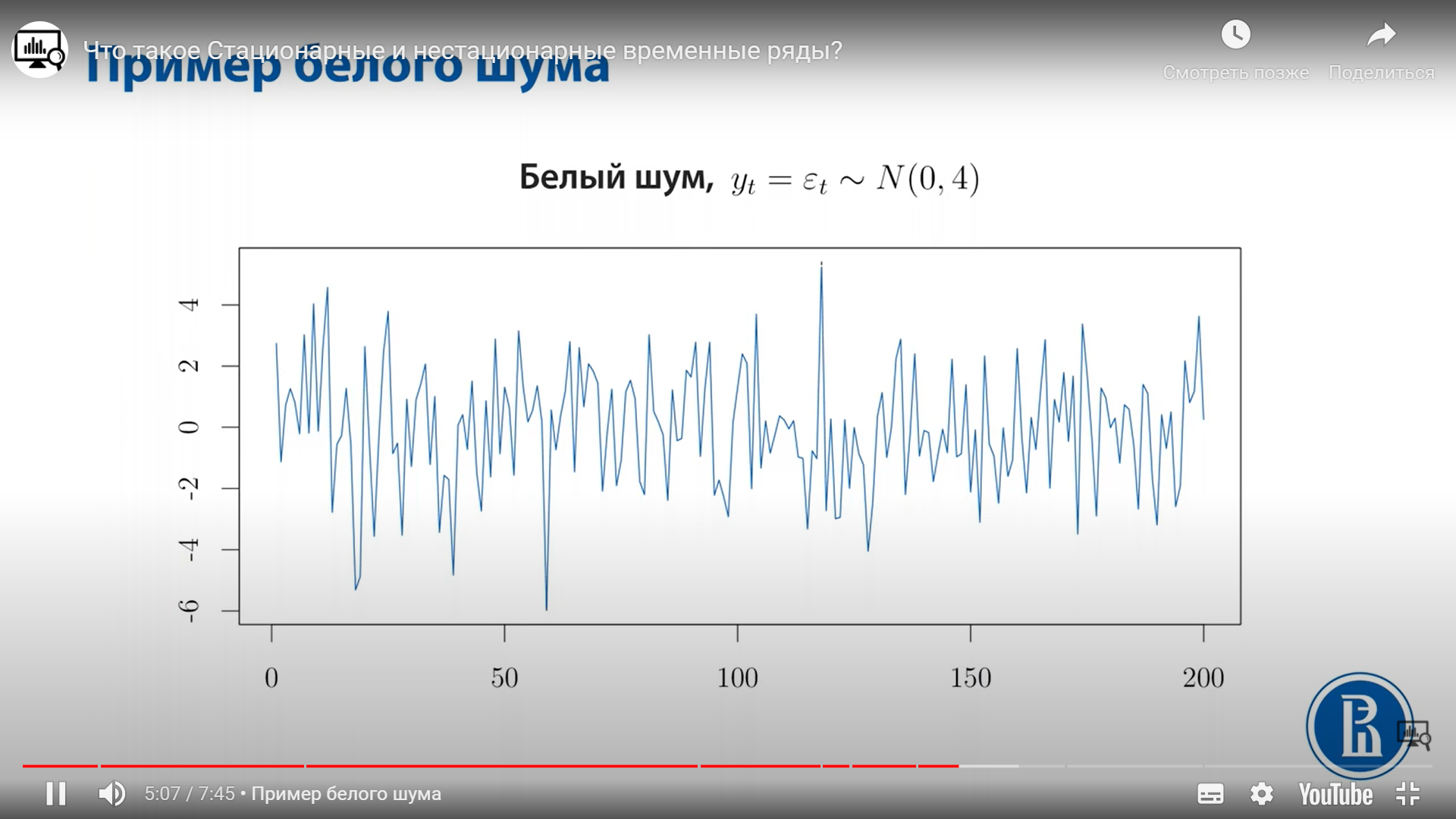
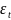– белый шум

Для стационарного ряда необходимо отсутствие в его структуре тренда и сезонной составляющей (если они есть – необходимо устранить), а также условие гомоскед-сти случ. остатка. Стацион. временной ряд:

Нестационарные ряды – временные ряды, в которых хотя бы одна из вероятностных характеристик непостоянна.

Примеры нестационарного процесса:

1) случайное блуждание

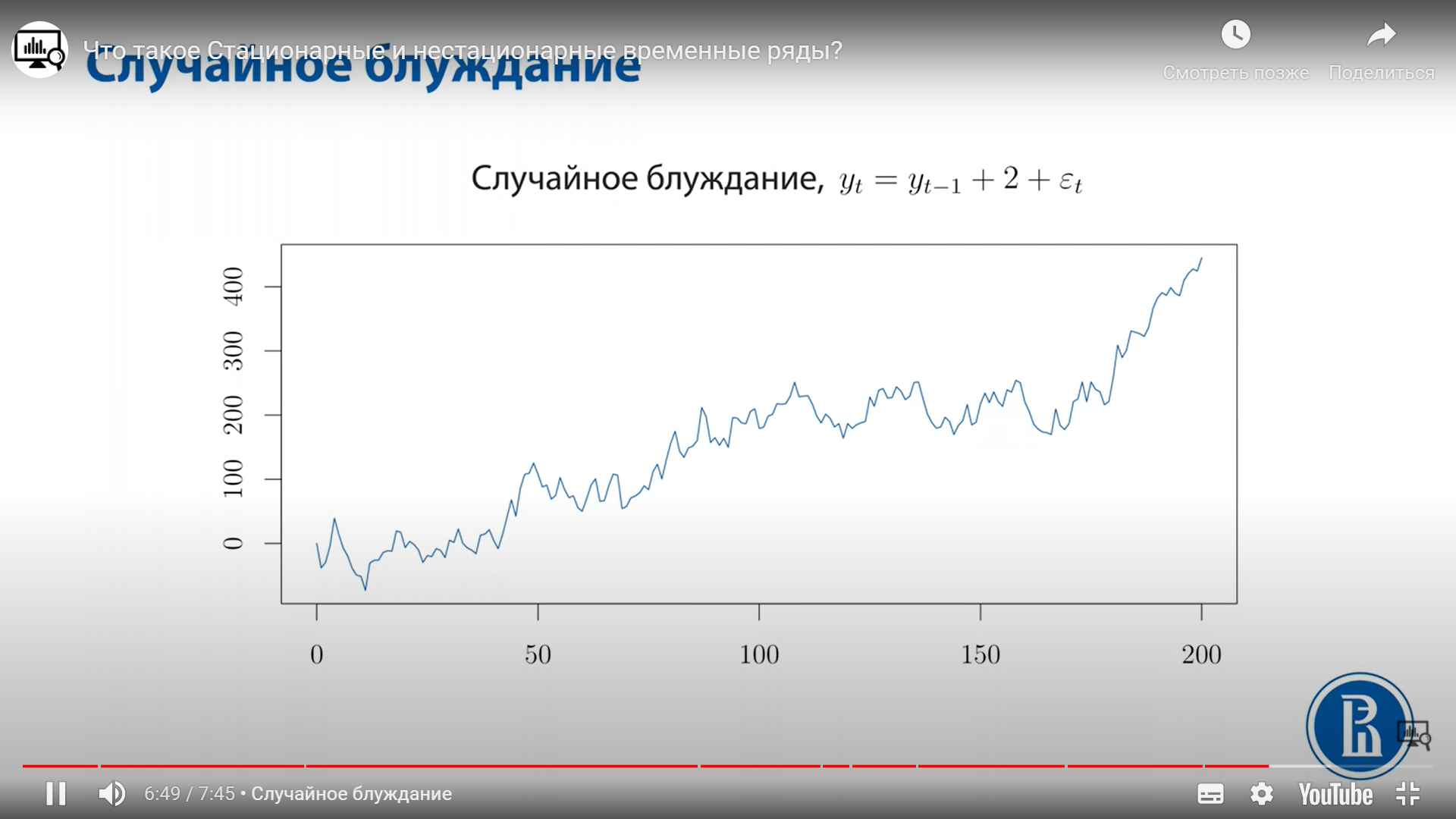
Чем дальше этот процесс отходит по времени, тем менее мы уверены в том, что она будет находиться в окрестности нуля.

26. Методика построения регрессионной модели на нестационарных временных рядах.

Нужно нестационарный временной ряд сделать стационарным. Опасность в случае нестац. врем. рядов – мнимая регрессия.

Признаки мнимой регрессии:

1) высокое значение R²

2) Малое значение DW

Ряд y_t (x_t) – стационарный, если среднее, дисперсия, ковариация ряда не зависят от времени t (нет T, S, E).

Если есть T(тренд) или S(сезонная компонента) – нужно устранить.

Способы избавления от T:

1) выделение в ряду тренда и построение ряда по отклонениям от тренда

2) Взятие разностей. Если в ряду есть линейный тренд – можно взять первые разницы (абсолютный прирост)

Замечания:

• рекомендуется строить регрессию на врем. ряд., используя прирост показателей, индекс роста

• если Т в форме параболы 2-го порядка, то для его устранения берут разность 2-го порядка

• если экспоненциальный или степенный Т, то метод последовательных разностей применяется не к исходному уровню ряда, а к их логарифмам.

3) если ряд зависимых показателей y_t содержит линейный тренд, а ряд фактора x_t (независ. показат.) стационарен, то исслед. модель: y_t = a + b₁x_t + b₂t + ε_t

27. Понятие авторегрессионной модели: общий вид модели, набор статистических характеристик. Формирование поля входных показателей для построения модели с помощью надстройки «Анализ данных» в среде Excel.

Авторегрессионная модель — модель временных рядов, в которой значения временного ряда в данный момент линейно зависят от предыдущих значений этого же ряда.

Общий вид:

Авторегрессионная модель порядка p (AR(p)):

y_t = a₁y_t-1 + a₂y_t-2 +…+ a_py_t-p + ε_t

Для порядка p=1 AR(1) модель авторегрессии называется марковским процессом:

y_t = ay_t-1 + ε_t

Используем МНК когда:

1) параметр при лаговой зависимости перем. меньше 1, то етсь

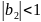
2) отсутствует автокорреляция остатков ε_t – используется h-стат. Дарбина-Уотсона (на основании коэффициента DW)

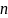– число наблюдений

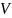– квадрат стандартной ошибки параметра при лаговой результативной переменной

Если 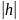>1,96 то автокорреляция отсутствует (уровень значимости 5% и большое количество наблюдений)

28. Понятие эконометрической модели с распределенными лагами: экономическая постановка задачи, общий вид модели, набор статистических характеристик. Формирование поля входных показателей для построения модели с помощью надстройки «Анализ данных» в среде Excel.

Динамическая экономическая модель – если она учитывает знач. входящих в неё переменных, относится как к текущим, так и к предыдущим моментам времени.

Величина S характер. запаздывание в воздействии фактора на результат – лаг.

Временные ряды самих факторных переменных, сдвинутых на 1 и более моментов времени – лаговые переменные.

Общий вид:

y_t = a + b₁x_t + b₂x_t-1 + ε_t – модель распред. лагов DL (1) (в скобках максимальный лаг)

y_t = a + b₁x_t-1 + b₂x_t-1 + ε_t – авторегресс. модель распред. лагов ADL (1, 1) (макс. лаг экзо- и эндогенных переменных)

Стат. характеристики:

Ориентир. на t -ст:

y_t = a + bx_t-1

Лаг S определяется по R² и t -ст.

1)

1-6

d_i – разность между рангами x и e (остатков)

2) Находим t-стат:

t_стат=

– есть гетероскедастичность остатков.

( , где – уровень значимости (=0,05)

Если t -ст указывает на незначимость – исключаем этот регрессор.