10. Проверка качества парной нелинейной регрессии: значимость параметров, адекватность модели.

Коэффициент детерминации используется для оценки качества уравнения регрессии. На сколько % уравнение регрессии объясняет поведение y.

Для оценки статистической значимости коэффициентов регрессии рассчитываются t-критерий Стьюдента. Если t>tкр, то коэффициенты статистически значимы.

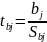
Для проверки значимости индекса детерминации используется F-статистика:

n – объем выборки

m – число параметров при независимых переменных.

11. Прогнозирование на основе парной нелинейной регрессии (степенная функция). Экономическая интерпретация параметров парной регрессии в степенной форме связи.

Прогнозирование – построение оценки зависимой переменной для таких значений независимых переменных, которых нет в исходных наблюдениях.

В экономической статистике достаточно широкое распространение получила степенная функция  . Ее особенность заключается в том, что параметр b в ней является коэффициентом эластичности и не зависит от факторов. Он характеризует, на сколько процентов изменится в среднем значение фактора у при изменении фактора х на 1%. Для большинства других экономических функций коэффициент эластичности определяется более сложно и часто зависит от х.

Для оценивания качества описания взаимосвязи факторов нелинейной модели регрессии используется Коэффициент детерминации. Он изменяется от 0 до +1. Чем ближе значение этого показателя к 1, тем лучше нелинейная модель соответствует фактически наблюдаемой зависимости.

12. Множественная линейная регрессия: аналитическое представление, остатки модели, методика оценки параметров модели. Формирование поля входных показателей для построения модели с помощью надстройки «Анализ данных» в среде Excel.

Множественной называют линейную регрессию, в модели которой число независимых переменных две или более.

Модель множественной линейной регрессии имеет вид:

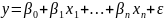
ɛ - случайная ошибка модели.

Уравнение множественной линейной регрессии имеет вид:

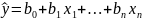
Как и в простой линейной регрессии, параметры модели bn вычисляются при помощи МНК. Переменные Х₁,Х₂,…,Х_k должны быть некоррелированы (линейно независимы) друг с другом.

EXCEL: Выберите «Сервис» и «Анализ данных». При появлении окна «Анализ данных» - нажмите курсором на инструмент анализа: «Регрессия»

В категории Входные данные окна «Регрессия» необходимо указать:

- Входной интервал Y – диапазон зависимых переменных, состоящих из одного столбца;

- Входной интервал Х - диапазон независимых переменных, подлежащих анализу. Может состоять из одного или более столбцов. Максимальное количество столбцов равно 16;

- Остатки (остатки, стандартизированные остатки, график остатков и график подбора) – используются как дополнительный анализ параметров вывода.

13. Свойства мнк-оценок множественной линейной регрессии: теорема Гаусса-Маркова.

Свойства оценок отклонений:

1. Оценки МНК являются функциями от выборки и их легко рассчитывать.

2. Эмпирическая прямая всегда проходит через точку (Хср., Yср).

3. Сумма отклонений (е) и среднее значение отклонения равны нулю.

4. Случайные отклонения не коррелированны с наблюдаемыми значениями зависимой и независимой переменной.

Теорема Гаусса-Маркова: для того, чтобы полученные оценки были несмещенными и состоятельными выполняется:

1.

2.Дисперсия остатков постоянна

3.Остатки некоррелированы

4.Остатки имеют норм.закон распределения

5.Факторы некоррелированы