Предмет и задачи эконометрики. Примеры экономических задач, решаемых с помощью аппарата эконометрики.
Экономико-математическое моделирование – это комплекс математических, экономических и научных дисциплин, предметом исследования которых являются количественные закономерности процессов, рассматриваемых в неразрывной связи с их качественными характеристиками.
Основные задачи эконометрики:
1. Построение эконометрических моделей, т.е. представление экономических моделей в математической форме, удобной для проведения эмпирического анализа.
2. Оценка параметров построенной модели
3. Проверка качества найденных параметров модели и самой модели в целом.
4. Использование построенных моделей для объяснения поведения исследуемых экономических показателей, прогнозирования и предсказания, а также для осмысленного проведения экономической политики.
Типовые экономические модели, изучаемые с помощью эконометрических методов:
производственные функции, выражающие взаимосвязи между затратами и результатами производственной деятельности;
модели функционирования национальной экономики;
целевые функции потребительского предпочтения и функции спроса;
модели рынка и экономического равновесия и др.
Стохастическая зависимость и функциональная зависимости. Диаграмма рассеяния и линия регрессии. Аналитическое описание линии регрессии.
Сущ. 2 вида зависимостей между явлениями:
При функциональной зависимости каждому значению независимой переменной х однозначно соответствует вполне определенное значение зависимой переменной у. Эту зависимость можно описать в виде равенства у = f(x) .
Стохастическая зависимость, то есть для независимой переменной x можно указать ряд значений зависимой у. Например, нет строгой зависимости между доходом и потреблением, ценой и спросом и т. д. Данная зависимость проявляется только в массовых явлениях. Это связано с тем, что зависимая переменная, кроме выделенной переменной х, подвержена влиянию также других неконтролируемых или неучтенных факторов.
При анализе зависимости между 2 переменными применяют диаграмму рассеяния, которая является наглядной формой представления инф. Для ее построения используют прямоугольную систему координат, где по оси абсцисс отмечают значения независимой переменно, а по оси ординат – значения зависимой переменной. Результат каждого наблюдения отображается точкой на плоскости. Скопление этих точек определяет картину зависимости 2 переменных. Диаграмма рассеяния – форма систематизации материала. По ширине разброса точек и можно сделать вывод о степени тесноты связи, если точки расположены близко друг к другу – наличие тесной связи.
Линия, которая аппроксимирует (приближает) такую стохастическую зависимость – линия регрессии
Функция
линейной регрессии
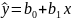
Параметр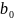 
в
модели парной регрессии – это среднее
значение зависимой переменной 
при
условии, что независимая переменная
равна
нулю.
Параметр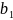 
в
модели парной регрессии – это коэффициент
модели регрессии. Значение
параметра характеризует, насколько
в среднем изменится зависимая
переменная
при
изменении
факторной переменной
на
единицу своего измерения.