30. Проверка наличия автокорреляции.

Наличие или отсутствие автокорреляции проверяют с помощью статистики Дарбина-Уотсона

Для проверки наличия автокорреляции используют процедуру проверки гипотез:

1)Формируется гипотеза Н0 об отсутствии автокорреляции Н0: р=0 и альтернативные гипотезы Н1:р>0 о наличии положительной автокорреляции и Н2:р<0 о наличии отрицательной автокорреляции

2)Выбирается уровень значимости α=0,05

3) по таблице распределения DW на основании α, n и k находят критические точки d1 и d2

4) На основании выборочных данных для построения регрессии по формуле рассчитывается значение статистики DW:

- если 0<DW<d1, то с вероятностью 1-α принимается гипотеза Н1

- если d1<DW<d2, то нет оснований для принятия или непринятия всех гипотез

- если d2<DW<4-d2, то с вероятностью 1-α принимается гипотеза Н0

- если 4-d2<DW<4-d1, то нет оснований для принятия или непринятия всех гипотез

- если 4-d1<DW<4, то с вероятностью 1-α принимается гипотеза Н2

Если DW попадает в зону неопределенности, то для обнаружения автокорреляции используются другие методы. Если утверждается наличие автокорреляции, то тогда пытаются ее устранить.

31 Понятие и структура временных рядов.

Временные ряды представляют собой совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени.

Момент (или период) времени обозначают t, а значение показателя в момент времени обозначают у(t) и называют уровнем ряда.

Каждый уровень временного ряды формируется под воздействием большого числа факторов, которые можно разделить на 3 группы:

1)Длительные, постоянно действующие факторы, оказывающие на изучаемое явление определяющее влияние и формирующие основную тенденцию ряда – тренд T(t).

2)Кратковременные периодические факторы, формирующие сезонные колебания ряда S(t).

3)Случайны факторы, которые формируют случайные изменения уровней ряда ε(t).

Аддитивной моделью временного ряда называется модель, в которой каждый уровень ряда представлен суммой тренда, сезонной и случайной компоненты:

. (1)

Мультипликативная модель – это модель, в которой каждый уровень ряда представляет собой произведение перечисленных компонент:

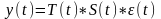. (2)

Выбор одной из моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний примерно постоянна, то строят аддитивную модель. Если амплитуда возрастает, то мультипликативную модель.

Основная задача эконометрического анализа заключается в выявлении каждой из перечисленных компонент.

32 Дисконтирование по простым процентам

В финансово-банковском деле часто приходится решать задачи обратные задачам начисления процентов:Какой должна быть исходная сумма Р , чтобы через некоторое время наращенная сумма была равна S. Такая ситуация часто возникает при разработке проектов и при учете платежных обязательств. В зависимости от двух ситуаций различают: математическое дисконтирование и банковский учет.

Матем. дисконт представляет собой решение след. задачи: какой должна быть первоначальная сумма Р , чтобы в будущем, положив в банк на срок n под простой процентную ставку, она дала сумму S.Из формулы простого процента получаем формулу:

P=S/(1+n *i)

Сумма Р наз. текущей или современной величиной, а сумма S- будущей величиной.

Пусть S- сумма указанная в платежном обязательстве, банк приобретает это платежное обяз-во у ее владельца до наступления срока платежа, по цене Р меньшей суммы S(учитывает платежное обяз-во с дисконтом), при наступлении срока платежа банк получил суммы S,указанную по плат. об-ву.

Дисконт= S-Р

Для расчета дисконта исп-ся спец. учетная ставка d,проценты начисл-ся на сумму S, т.е. дисконт равен: S-Р= S*n*d,гдеd- учетная ставка

n- срок от даты учета платежного обяз-ва до даты его погашения

Р= S-( S*n*d)= S(1-n*d) – сумма ,которую банк уплачивает владельцу