25. Прогнозирование на основе множественной регрессии.

Как и в парной регрессии для множественной регрессии различают точечный прогноз и интервальный прогноз. Точечный прогноз (число) получают при подстановке прогнозных значений независимых переменных в уравнение множественной регрессии. Обозначим через:

(12)

вектор прогнозных значений независимых переменных, тогда точечный прогноз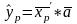 (13)или 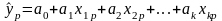(14)

Стандартная ошибка предсказания в случае множественной регрессии определяется следующим образом: (15)

Выберем уровень значимости α по таблице распределения Стьюдента. Для уровня значимости α и числа степеней свободы ν = n-k-1 найдем t_кр. Тогда истинное значение у_р с вероятностью 1- α попадает в интервал:

(16)

26. Понятие гетероскедастичности

Вторая предпосылка регрессионного анализа гласит, что дисперсия случайного члена регрессионной модели может быть постоянной для любого наблюдения, т.е.:

Это условие называется гомоскедастичностью (одинаковой разбросанностью).

Зависимость дисперсии случайного члена от номера наблюдения называется гетероскедастичностью,

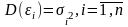
А) гомоскедастичность Б) гетероскедастичность

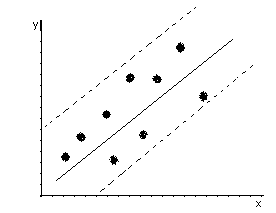
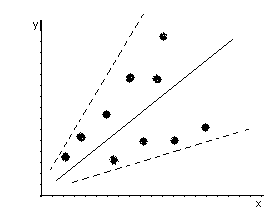
Для обнаружения гетероскедастичности используются различные тесты. Например, тест ранговой корреляции Спирмена, тест Гольдфельда-Квандта. При наличии гетероскедастичности для оценки параметров регрессионной модели используют обобщенные (или взвешенный МНК).

27. Тест Гольдфельда-Квандта.

Для обнаружения гетероскедастичности используется тест Гольдфельда-Квандта. Предполагает что r_iпропорциональнаXi (разброс увеличивается с увеличением х):

1)Все n наблюдения в выборке упорядочиваются по возрастанию переменной Х

2)Оцениваются отдельные регрессии для первых n0 и для последний n0 наблюдений . Средние (n-2n0) наблюдений отбрасываются.

3)Составляется статистика:

F=S2/S1, где S1=Σe_i²

S2=Σe_i²

4) Формируется нулевая гипотеза об отсутствии гетероскедастичности

Для уравнения значимости 2 находим Fпр. Если F>Fпр, то нулевая гипотеза об отсутствии гетероскедастичности отклоняется, если предполагается что ri обратно пропорционально Xi, то составляется статистика F=S1/S2

28. Обобщенный мнк.

Предположим, что имеет место гетероскедастичность, постоим парную линейную регрессию.

П редположим что

Уравнение регрессии будет иметь вид:

Разделим обе части этой модели на :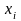

В последней модели случайная ошибка ε не зависит от объясняющей переменной . Сделаем замену переменных:

Получим регрессионную модель:

,

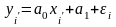для которой применим классический МНК.

29. Понятие автокорреляции

Автокорреляция – зависимость текущего значения случайного члена от непосредственно предшествующих значений. Т.о. автокорреляция нарушает 3 предпосылку регрессионного анализа.

Причинами автокорреляции может быть:

-неправильно выполненная спецификация (неправильно подобрана математическая функция, описывающая исследуемую зависимость)

-ошибки в исходных наблюдениях

-не включение в уравнение регрессии фактора, который оказывает влияние на зависимую переменную

Наличие или отсутствие автокорреляции проверяют с помощью статистики Дарбина-Уотсона