- •1. Основные понятия эконометрики
- •2. Понятие и виды регрессий.
- •3. Основные этапы построения регрессий
- •4.Суть метода наименьших квадратов
- •5. Вывод формул для расчета коэффициентов парной линейной регрессии
- •6. Экономическая интерпретация коэффициентов парной линейной регрессии
- •7. Основные предпосылки регрессионного анализа
- •8. Теорема Гаусса-Маркова
- •9. Стандартные ошибки коэффициентов регрессии
- •10. Проверка значимости коэффициентов регрессии
- •11. Прогнозирование
- •12. Построение интервального прогноза в случае парной линейной регрессии.
- •13. Коэффициент детерминации
- •14. Коэффициент корреляции
- •15. Проверка значимости коэффициента детерминации
- •16. Проверка значимости коэффициента корреляции.
- •17.Регрессии, нелинейные по переменным
- •18. Регрессии, нелинейные по параметрам.
- •19 Проверка качества нелинейной регрессии и тесноты связи ее переменных.
- •20. Коэффициент эластичности.
- •21. Понятие мультиколлинеарности.
- •22. Множественная регрессия и расчет ее параметров.
- •23. Экономическая интерпретация коэффициентов множественной регрессии.
- •24. Коэффициенты эластичности для множественной регрессии.
- •25. Прогнозирование на основе множественной регрессии.
- •26. Понятие гетероскедастичности
- •27. Тест Гольдфельда-Квандта.
- •28. Обобщенный мнк.
- •29. Понятие автокорреляции
- •30. Проверка наличия автокорреляции.
- •31 Понятие и структура временных рядов.
- •32 Дисконтирование по простым процентам
- •33 Сложный процент
- •34 Переменная процентная ставка и дробное число лет.
- •35 Сложный процент и наращение процентов m раз в год
- •36.Эффективная ставка и непрерывное наращение процентов
- •37.Финансовая эквивалентность обязательств и конверсия платежей
- •38.Учет инфляции при измерении доходности финансовых операций
- •39. Вывод зависимости между реальной и номинальной процентными ставками
- •40. Текущая и чистая текущая стоимости инвестиционных проектов
- •41. Зависимость чистой текущей стоимости от ставки дисконта
- •42. Внутренняя норма доходности инвест. Проекта
- •43. Индекс рентабельности проекта
- •44. Сравнение методов npv и irr
- •45. Модель оптимального выбора проектов с учетом дополнительных ограничений
- •46. Анализ эффективности инвестиционных проектов с учётом риска
- •48. Критерий Сэвиджа
- •49. Критерий Гурвица.
- •50. Критерий Вальда.
- •52. Характеристики ценных бумаг и их статистические оценки
- •53. Портфель ценных бумаг и его характеристики
- •54. Зависимость риска портфеля от диверсификации
- •55. Эффективные портфели, модели Марковица.
- •56. Экономическая интерпретация решения задач Марковица
- •57. Коэффециентb(бетта)
- •58. Модель оценки финансовых активов (сарм)
- •59. Коэффициенты α (альфа)
- •Современные методологии оценки рыночного риска
- •61. Дельта-нормальный метод
- •62. Метод исторического моделирования (мим)
17.Регрессии, нелинейные по переменным
Регрессии, нелинейные по переменным- многочлены различных степеней, обратные функции (гипербола), уравнения с корнями.
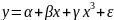 (1)
(1)
 (2)
(2)
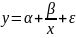 (3)
(3)
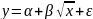 (4)
(4)
Перед построением нелинейных регрессий по переменным выполняют их ЛИНЕАРИЗАЦИЮ путём замены переменных.
В
1 уравнении:

Во
2 уравнении:

В
3 уравнении:
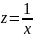
В
4 уравнении:
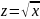
После линеаризации с помощью метода наименьших квадратов оцениваются параметры получившейся регрессии.
18. Регрессии, нелинейные по параметрам.
-
экспоненциальная

-
степенная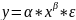
-показательная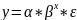
Нелинейные регрессии по параметрам линеаризуются с помощью ЛОГАРИФМИРОВАНИЯ:

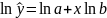

После логарифмирования выполняется замена переменных, строятся уравнения линейных регрессий, после чего выполняется ПОТЕНЦИИРОВАНИЕ.
19 Проверка качества нелинейной регрессии и тесноты связи ее переменных.
Для оценки степени нелинейной зависимости используется индекс корреляции.Индекс корреляции вычисляется о формуле:

Индекс корреляции (R) меняется от 0 до 1. чем ближе R к 1, тем сильнее нелинейная связь между переменными, чем ближе к 0, тем нелинейная зависимость слабее.
Для оценки качества регрессии используется коэффициент детерминации, рассчитывается по формуле:
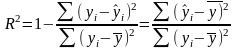
Меняется от 0 до 1.
Чем ближе к 1, тем выше качество регрессии. Чем ближе к 0 , тем качество регрессии ниже.
Для проверки значимости коэффициента детерминации используется F-статистика

n – объем выборки
m – число параметров при независимых переменных.
Так для параболы m=2, а для степенной функции m=1
20. Коэффициент эластичности.
В экономическом анализе часто используется эластичность функции. Эластичность функции рассчитывается как относительное изменение у к относительному изменению х:
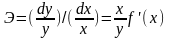
Эластичность показывает, насколько процентов изменяется зависимый показатель y при изменении фактора x на 1 %.
Для степенной
функции
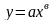 эластичность представляет собой
постоянную величину, равную в,
действительно:
эластичность представляет собой
постоянную величину, равную в,
действительно:

Для остальных
функций эластичность не является
постоянной величиной. Так для линейной
функции
 эластичность
эластичность
 ,
т.е. эластичность зависит от х, поэтому
для остальных функций вычисляется
средний показатель эластичности, в
частности для линейной функции по
формуле:
,
т.е. эластичность зависит от х, поэтому
для остальных функций вычисляется
средний показатель эластичности, в
частности для линейной функции по
формуле:
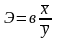
21. Понятие мультиколлинеарности.
Одним из условий регрессионного анализа является предположение о линейной независимости объясняющих переменных. Однако, может оказаться, что несколько или все объясняющие переменные могут иметь общий временной тренд, относительно которого они совершают малые колебания. Тогда условие линейной независимости объясняющих переменных нарушается.
Мультиколлинеарность– высокая взаимная коррелированность (линейная зависимость) объясняющих переменных. Различают функциональную и стохастическую мультиколлинеарность.
При функциональной мультиколлинеарности определитель матрицы X’X равен 0. В этом случае невозможно решить матричное уравнение (3).
При стохастической мультиколлинеарности определитель матрицы X’X очень мал. Она имеет место, когда хотя бы между двумя объясняющими переменными существует тесная корреляционная связь).
Для определения наличия мультиколлинеарности существуют 2 способа:
Рассчитывается матрица коэффициентов парной корреляции. Если между какими-либо независимыми переменными коэффициент парной корреляции больше 0,8, то считают, что мультиколлинеарность имеет место.
Рассчитывают определитель матрицы X’X и его близость к 0 также свидетельствует о наличии мультиколлинеарности.
Методы устранения мультиколлинеарности:
Из двух объясняющих переменных, имеющих высокий коэффициент корреляции, исключают из рассмотрения ту, которая имеет меньший коэффициент корреляции с зависимой переменной.
Метод включения: независимая переменная включается в уравнение регрессии в том случае, если включение существенно увеличивает значение коэффициента множественной корреляции.
Метод исключения: после построения уравнения регрессии проверяется значимость всех коэффициентов. Из уравнения исключаются независимые переменные с незначимым коэффициентом. Затем получают новое уравнение регрессии и опять проводят оценку значимости коэффициентов.