10. Проверка значимости коэффициентов регрессии

При проверке значимости коэффициентов регрессии мы проверяем действительно ли они существенно(значимо) отличны от нуля, т.к. если коэф-т 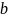на самом деле близок к нулю, то значит не оказывает никакого влияния на и построение регрессии не имеет смысла.

Для проверки значимости используют процедуру проверки гипотез на примере коэффициента .

1) Формулируется гипотеза : R²=0, состоящая в том, что истинный параметр

2)В качестве критерия проверки гипотезы принимают случайную величину t:

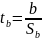(1)

Эта случайная величина имеет распределение Стьюдента с υ=n-2 степенями свободы. Подставим в формулу (1) оценённое по выборке значение коэф-та в и его стандартную ошибку 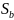, получим наблюдаемое или расчётное значение t-критерия tрасч.

3)Выберем уровень значимости проверки гипотезы α=0,05 или α=0,01, т.е пятипроцентный или однопроцентный уровень значимости. (Уровень значимости определяет вероятность . с которой мы будем принимать или отвергать нулевую гипотезу).

4)По таблице распределения Стьюдента для выбранного уровня значимости α/2 и υ=n-2 находят tкр.

5) Если |tрасч|˃tкр, то гипотеза Hо о равенстве параметра β=0 отвергается параметр β существенно отличен от нуля, коэф-т в значим, а переменная х оказывает существенное влияние на зависимую переменную у (гипотеза Hо считается не верной с вероятностью 1-α).

6) Если |tрасч| ˂tкр, гипотеза Hо принимается, коэф-т в незначим, и переменная Х не оказывает существенного влияния на зависимую переменную у.

11. Прогнозирование

Различают точечное прогнозирование и интервальный прогнозирование.

Точечный прогноз-значение зависимого показателя, который россчит-ся путем подстановки заданных значений независимых показателей в ур-ние регрессии.

Интервальный прогноз – доверительный интервал, в который с заданной вероятностью попадает истинное значение зависимого показателя для заданных значений независимых показателей.

12. Построение интервального прогноза в случае парной линейной регрессии.

В интервальном прогнозе находят интервал, в котором с заданной вероятностью попадает истинное значение объяснимой переменной для заданного прогнозного значе-я объясн. переменной.

Рассмотрим теоретическую регр. Модель y=L+βx +E

и составим выборочное уравнение регрессии: =a+bx

Через Yp и Xp обозначим прогнозные значения ,соот-но зависимой и независимой переменно ,т.еyp= L+βxp+E

Через p обозначают оценку истинного прогнозного значения зависимой переменной: Т.е p=a+bxp

Ошибкой предсказания(Δp )показывает разность между прогнозируемым и истинным значением зависимой переменной. Δp= p-yp

Можно показать, что Д(Δp)=(1+ * (1)

Заменим на его оценку и увеличим

Заменим в 1формуле.

Sp=S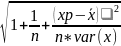 (2);Sp- наз-ют стандартной ошибкой предсказания

Выберем ур-нь значимости L ,найдем tкрет. , тогда можно доказать что с вероятностью 1-L истинное прогнозное значение зависим. показ-я yp попадает в интервал. p –tкр*Sp<yp< p+tкр*Sp

Вернемся к примеру 1 и найдем точечный интервал прогноз. прибыли банка, в случае ,или объем привлеч. ресурсов=20млн.ден.ед.

Осущ. точечный прогноз в построенном уравнении регр. подставим вместо 20 ; p= -1,75+0,775*20=13,75

Вывод: Если объем привл. ресурсов достигнет 20млн.дн.ед,то сред.прибыль банка составит 13,75млн.ден.ед.

Интервальный прогноз

S=1.816 n=5, xp=20, ̅x =10, var(x) =32

Sp=1.816

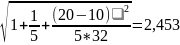
L=0.05 V =5-2=3, tкр=3, 18

13, 75-3, 18* 2,453<yp<13, 75+3, 18+2,453

5,948<yp<21,5

Вывод: можно утверждать, что с вероятностью 0,95 истинное значе-е прибыли банка при объеме привлеченных ресурсов 20млг.ден.ед.