45. Модель оптимального выбора проектов с учетом дополнительных ограничений

Пусть инвестор рассматривает m инвестиционных проектов одинаковой продолжительности. Каждый из проектов требует первоначальных инвестиций Ioi и имеет чистую текущую стоимость NPVi, i=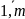 . инвестиционные возможности инвестора ограничены суммой Io. Кроме финансовых, инвестиционные проекты требуют и других ресурсов, объемы которых ограничены. Обозначим через - количество ресурса i-го вида, необходимое для проекта j: i= , j= , а также через -общий объем ресурса вида i, имеющийся в наличии. Необходимо выбрать проекты таким образом, чтобы уложиться в имеющиеся ресурсы и чтобы сумма чистых текущих стоимостей проектов была максимальной/

Математическая модель имеет вид:

Пусть переменная = описывает j-ый проект

Определим модель след образом

= 1, если инвестор выбирает j-ый проект

0, если инвестор отвергает j-ы проект

Тогда функция , выражающая суммарную чистую текущую стоимость проектов будет иметь вид =

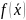Ограничения по первоначальным инвестициям

А по другим ресурсам:

В итоге имеем модель оптимального выбора инвестиционного проекта с учетом доп ограничений: ; ;

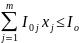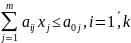
Иногда проекты взаимосвязаны друг с другом. Например, из двух проектов может быть выбран только один, это условие описывается неравенством

Проект может быть принят лишь в том случае, кода будет принят проект 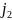. Тогда в модель необходимо добавить неравенство

Или же из двух проектов должен быть выбран хотя бы один:

46. Анализ эффективности инвестиционных проектов с учётом риска

В современном инвест. анализе денежный поток считают случайной величиной. Вероятность принятия ден. потоком точного значения оценивают либо экспертом либо на основ.данных об аналогичных проектов с тем же урав-м риска и когда ден. потоки считают случайными величинами, то говорят об анализе эффект-ти инвест. проектов в условии риска.

Обозн-м через Xtзнач-я ден. потока в период t=1,n(сверху поставь среднее знач), n- число периодов реализ. проектов.

Пусть Xtявл-ся случайной величиной и принимает знач-е Xt1,Xt2,….Xtn с соответствующими вероятностями pt1,pt2,….ptn.

Тогда эффек-ть проекта оценивают с помощью матем. ожидания NPV:

E (NPV)=

r-ставка дисконтирования.

В современной литературе для обознач. матем. ожидания испол-ют букву Е.

E(Xt)=

А риск проекта рассч-ся вариацией проекта кот.рассч-ся по формуле:

V(NPV)=

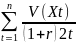
Если ден. потоки явл-сянезав-ми случ-ми величинами.

И если ден. потоки явл-ся зависимыми случ-ми величинами:

V(NPV)=

V(Xt)=

Проект характер-ся двумя величинами матем. ожиданий NPV, выражающей доходность проекта и вариаций NPV выражает его риск.

48. Критерий Сэвиджа

Этот критерий основан на принципе минимизации максимального риска. Риском r_ij, , , 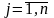принимающего решение называют разницу между тем выигрышем, который он бы получил, если бы знал, какое состояние реализует природа и его реальным выигрышем, то есть,

r_ij=β_ij – 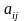, где .

Матрица рисков R имеет вид:

П₁ П₂ … П_n

А₁r₁₁r₁₂ … r_1n

А₂r₂₁ r₂₂ … r_2n

R=

… … … … …

А_m r_m1 r_m2 … r_mn

Принимающий решение для каждой стратегии А_i находит максимальный риск r_i, r_i= . Затем из максимальных рисков выбирает минимальный:

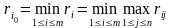(6.4.2)

Стратегия А_i0, соответствующая минимальному из максимальных рисков r_i0, будет наилучшей по Сэвиджу.