41. Зависимость чистой текущей стоимости от ставки дисконта
Из формулы для расчета NPV видно, что завис-тьNPV от ставки дисконта явл-ся нелинейной. Рассмотрим NPV как функцию от r и рассчитаем 1-ую и 2-ую производную.
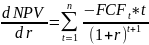
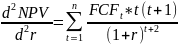
Предположим, что свободные ден. потоки в любом году неотрицательные, т.е поступление от пректа> доп. инвестиций в проект.
Если своб. ден.
потоки неотриц, то 1-ая произовдная
<
0, а 2-ая производная > 0. Тогда с ростом
ставки дисконтир-я r
значение NPV
монотонно убывает, а график ф-цииNPV
будет выпуклым вниз. Зависимость выглядит
след.образом:
NPV
завис-тьNPV от r в случае неотриц. своб. ден. потоков
IRR
r
Если среди своб. ден. потоков проекта есть отриц. (поступления < доп. инвестиций), то завист-тьNPV от ставки дисконта не будет монотонной, величина NPV может неск. раз менять знак с ростом ставки дисконта r. Графически завис-ть можно изобр-ть след образом:
NPV
завис-ть в случе произвольных ден. потоков
r
42. Внутренняя норма доходности инвест. Проекта
Из вышесказанного следует, что необходимо тщательно подходить к выбору ставки дисконтирования, в кот.обычно закладывают банковский процент, инфляцию и риск конкр. проекта.
Внутр норма доходности – ставка дисконтирования, при кот.чистая текущая ст-ть проекта (NPV) = 0. => для определения IRR следует решить уравнение:
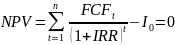
Чем больше IRR, тем эффективнее проект.
Т.к. в качестве ставки дисконтирования принимают внутр. норму доходности альтернатив.проектов с тем же уровнем риска, то IRR сравнивают со ставкой дисконтирования.
Если IRR> ставки дисконтир-я (внутр норма доходности исслед. проекта > альтернатив.проектов), то исследуемый проект эффективнее альтернативных и его следует принять. Если IRR< ставки дисконтир-я, то альтерн. проекты более эффективны, исслед. проект следует отклонить.
43. Индекс рентабельности проекта
Индекс рентабельность PI показывает, сколько единиц приведенных к начальному моменту поступлений от реализации проекта приходится на единицу приведенных к первоначальному моменту инвестиций, т.е.
PI=∑
/ ( ∑
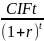+Io
)
Если приведенные поступления больше приведенных затрат PI>1,то проект эффективен, если PI<1, то не эффективен, если PI=1, то инвестору нужны доп аргументы, чтобы принять или отклонить проект
Например, PI=1,32. PI>1, следовательно проект принимается. Можно сделать вывод. Что на 1 д.е. приведенных инвестиций приходится 1,32 д.е. приведенных поступлений от реализации продукции.
44. Сравнение методов npv и irr
1) показатель NPV является абсолютной величиной и измеряется в д.е, поэтому если инвестиционный проект должен обеспечить возможно большую массу дохода, то используется NPV
2) для расчета величины NPV необходима ставка дисконтирования
Ставка дисконтирования должна адекватно отражать экономическую ситуацию (инфляцию, банковские % и риски), а ее определение представляет собой сложную задачу
3) для расчета IRR не требуется ставка дисконтирования
4) IRR является относительной величиной и измеряется в %, поэтому он более удобный для интерпретации и сравнения
5) IRR можно интерпретировать след образом:
-IRR можно рассматривать в качестве максимальной платы за источники финансирования проекта
-IRR можно рассматривать как нижний уровень прибыльности инвестиционного проекта
6) к недостаткам модели IRR относят трудности, связанные с вычислением данного показателя, со сложностью решения уравнения
Уравнение может иметь несколько решений, а может не иметь их вовсе.
В случае существования нескольких значений IRR принято выбирать меньшее
7) если свободные денежные потоки неотрицательны, то легко доказать, что NPV>0 тогда и только тогда, когда IRR>r