11. Множественная регрессия: спецификация модели.

Множественная регрессия является обобщением парной регрессии. Она используется для описания зависимости между объясняемой (зависимой) переменой У и объясняющими (независимыми) переменными Х1,Х2,...,Хk. Множественная регрессия может быть как линейная, так и нелинейная, но наибольшее распространение получила линейная множественная регрессия.

Теоретическая линейная модель множественной регрессии имеет вид:

соответствующую выборочную регрессию обозначим:

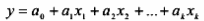
Как и в парной регрессии случайный член ε должен удовлетворять основным предположениям регрессионного анализа. Тогда с помощью МНК получают наилучшие несмещенные и эффективные оценки параметров теоретической регрессии.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность. Например, в модели урожайности качество почвы задается в виде баллов.

2. Факторы не должны быть коррелированы между собой и тем более находиться в точной функциональной связи.

Коэффициент множественной регрессии aj показывает, на какую величину в среднем изменится результативный признак Y, если переменную Xj увеличить на единицу измерения, т. е. является нормативным коэффициентом.

Для оценки коэффициентов множественной линейной регрессии с двумя независимыми переменными 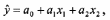, можно решить систему уравнений:

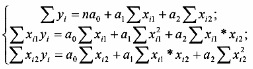
12. Множественна регрессия: статистические характеристики адекватности.

Для практического использования моделей регрессии большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным.

Анализ качества эмпирического уравнения множественной линейной регрессии начинают с построения эмпирического уравнения регрессии. Первое же, построенное по выборке уравнение регрессии, очень редко является удовлетворительным по тем или иным хар-кам. Поэтому следующей важнейшей оценкой является проверка качества уравнения регрессии. В эконометрике принята устоявшаяся схема такой проверки, которая проводится по следующим направлениям:

• проверка статистической значимости коэффициентов уравнения регрессии

• проверка общего качества уравнения регрессии

• проверка свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполнимости предпосылок МНК)

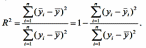Коэффициент детерминации (множественный), является мерой адекватности регрессионной модели и определяется так же, как и в случае парной регрессии:

Коэффициент детерминации характеризует долю вариации зависимой переменной, обусловленную регрессией. Чем ближе R2 к единице, тем лучше регрессия описывает зависимость между зависимой и объясняющими переменными. Скорректированный R2:

Оценка качества соответствия выборочного равнения регрессии наблюдаемым данным может производиться и с помощью средней ошибки аппроксимации A регрессии по формуле:

Коэффициент множественной корреляции (R) характеризует тесноту связи между результативным показателем и набором факторных показателей:

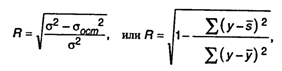, где где σ2 — общая дисперсия эмпирического ряда, характеризующая общую вариацию результативного показателя (у) за счет факторов; σост2 — остаточная дисперсия в ряду у, отражающая влияния всех факто­ров, кроме х;

Коэффициент множественной корреляции принимает только поло­жительные значения в пределах от 0 до 1. Чем ближе значение коэффи­циента к 1, тем больше теснота связи. И, наоборот, чем ближе к 0, тем за­висимость меньше.

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:

, где Sфакт - факторная сумма квадратов на одну степень свободы; Sост– остаточная сумма квадратов на одну степень свободы;……..

Гипотезу о стат значимости уравнения регрессии принимают, если Fкр<F при уровне надежности α=0,05 и степенях свободы df1=m и df2=n-m-1.

Оценка значимости коэффициентов чистой регрессии по t-критерию Стьюдента может быть определена по формуле:

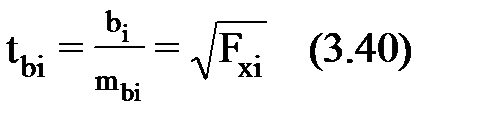где mbi (лучше заменить на Sbi) - стандартная ошибка коэффициента регрессии bi, bi-коэффициент регрессии перед xi, Fxi- частный критерий Фишера.