57. Многоканальная смо с огранич-й очередью и ее характеристики.

Пусть в n-канальную систему массового обслуживания поступает простейший поток требований с интенсивностью λ; число мест в очереди ограничено и равно m. Время обслуживания требований (для одного канала) экспоненциальное со средним значением tобсл . Пронумеруем состояния СМО по числу заявок, находящихся в системе:

S0 – система свободна, S1 – занят 1 канал, Sn – заняты все каналы, Sn+1 – заняты се каналы и одно место в очереди, Sn+m – заняты все каналы и все места в очереди.

Расчёт показателей эффективности СМО с ограничением на длину очереди:

Вероятности состояний P₀ =

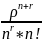P_k = *P₀ P_n+r = * P₀

Вероятность отказа P_отк = P_n+m = *P₀

Относительная пропускная способность q=1-P_отк

Абсолютная пропускная способность A = q* λ

Среднее число занятых каналов ͞N_з =

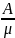
Коэффициент занятости каналов k_з =

Средняя длина очереди ͞L = P₀ * *

Среднее время пребываня в очереди ͞t_ож =

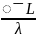
Среднее число требований, находящихся в системе ͞k = ͞N_з + ͞t_ож

Среднее время пребывания требования в системе ͞t_сист = ͞t_ож + q = ͞t_ож + q͞t_об

58. Многоканальная смо с неограниченной очередью и ее хар-ки.

Так как длина очереди не ограничена, то граф состояний в этом случае является бесконечным.

Установившийся режим работы системы существует при условии < 1, а в случае ≥ 1 система не справляется с обслуживанием и очередь будет расти неограниченно. Отношение называется уровнем загрузки системы. Полагаем, что < 1. Расчет показателей эффективности СМО без ограничений на длину очереди:

Вероятности состояний P₀=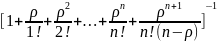

P_k = P₀

P_n+r = P₀

Вероятность отказа Р_отк = 0

Относительная пропускная способность q = I

Абсолютная пропускная способность Ф = λq = λ

Среднее число занятых каналов ͞N = = = ρ

Коэффициент занятости каналов k =

Средняя длина очереди ͞L =

Среднее время пребывания в очереди ͞t͞ =

Среднее число требований, находящихся системе ͞k = ͞N_з + ͞L_ож

Среднее время пребывания требования в системе ͞t = ͞t_ож + q

59. Многоканальная смо с отказами и ее характеристики.

Пусть в n-канальную систему массового обслуживания поступает простейший поток требований с интенсивностью . Время обслуживания требований (для одного канала) экспоненциальное, со средним значением t_обс.

Если требование поступает в систему в момент, когда все n каналов заняты, то оно получает отказ (покидает систему не обслуженным). Если же в момент поступления требования имеется хотя бы один свободный канал, то оно принимается к обслуживанию и обслуживается до конца. Найти предельные вероятности состояний системы и показатели ее эффективности.

Пронумеруем состояния СМО по числу заявок, находящихся в системе.

S₀ - система свободна

S₁ – занят один канал

…

S_n – заняты все каналы

Переходы из состояния S_k в состояние S_k+1 происходят под воздействием входящего потока заявок с интенсивностью λ. Переход из состояния S_k в состояние S_k-1 происходит под воздействием суммарного потока обслуживаний k каналами; интенсивность суммарного потока равна сумме интенсивностей слагаемых потоков.

Размеченный граф состояний системы без очереди представлен на рис:

Показатели эффективности:

Вероятности состояний:

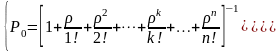
Вероятность отказа:

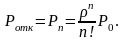
Относительная пропускная способ-ть (доля обслуженных заявок): q = 1- Ротк

Абсолютная пропускная способность (среднее число обслуживаемых заявок за единицу времени): А = q.

Среднее число занятых каналов:

Коэффициент занятости каналов: