37. Основные показатели эффективности инвестиционных проектов:

Чистая текущая стоимость (NPV) инвестиционного проекта показывает, на сколько денег в начальный момент времени нужно вложить меньше в инвестиционный проект, чем в банк для того, чтобы обеспечить последовательность платежей, равных свободным денежным потокам инвестиционного проекта.

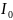NPV= - +PV

Очевидно, если NPV>0 – проект эффективен, NPV<0 – проект неэффективен, NPV=0 необходимо использовать другие критерии эффективности.

Внутренняя доходность инвестиционного проекта (IRR) – это такая банковская процентная ставка, при которой банковский начальный капитал, обеспечивающий последовательность платежей, равных (ожидаемым) свободным денежным потокам инвестиционного проекта, равен начальным инвестициям в проект. Таким образом, внутренняя доходность инвестиционного проекта – это процентная ставка r, при которой

=

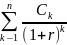Т.к. NPV= - +PV= + , то внутренняя доходность инвестиционного проекта – это такая ставка дисконтирования свободных денежных потоков инвестиционного проекта, при которой чистая текущая стоимость инвестиционного проекта равна нулю.

Модифицированная внутренняя норма окупаемости – уравновешивает дисконтированные инвестиции и наращенные поступления.

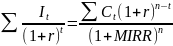
Срок окупаемости (PP) — период времени, необходимый для того, чтобы доходы, генерируемые инвестициями, покрыли затраты на инвестиции. Формула, к которой прибегают для расчёта простым способом вычисления коэффициента срока окупаемости выглядит так:

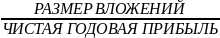РР = или РР = 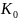 / ПЧсг

РР — срок окупаемости выраженный в годах.

 — сумма вложенных средств.

ПЧсг — Чистая прибыль в среднем за год.

Дисконтированный срок окупаемости инвестиций – срок окупаемости инвестиций в текущих стоимостях; определяется как время, которое требуется, чтобы инвестиции обеспечили достаточные поступления денег для возмещения инвестиционных расходов, при этом учитывается временная стоимость денег; точнее характеризует финансовый риск.

>

Свойства: NPV= =

Из вида этой функции следует, что она линейно зависит от всех своих аргументов, кроме процентной ставки. Коэффициенты линейной зависимости уменьшаются при росте r. Это означает, что прибыль, полученная на более ранних этапах, сильнее влияет на значение NPV. Зависимость NPV от процентной ставки является нелинейной. С ростом k значение NPV постепенно убывает. NPV обладает свойством аддитивности, что позволяет складывать значения NPV по различным проектам и использовать агрегированную величину для оптимизации инвестиционного портфеля. Справедлива следующая теорема: Если для некоторого инвестиционного проекта с регулярными поступлениями NPV>0, то справедливо неравенство IRR>r .И обратно: если IRR>r, то NPV>0.

Чувствительность инвестиционного проекта - изменение денежных потоков проекта в зависимости от изменения одного или нескольких. Методика анализа чувствительности денежных потоков заключается в следующем:

1. устанавливается зависимость денежных потоков от факторов, влияющих на него;

2. рассчитываются денежные потоки по годам, находят NPV и IRR;

3. определяют частную производную по каждому фактору, который показывает, на сколько денежных единиц изменится денежный поток при увеличении данного фактора на единицу.

38. Оценка проектов в условиях риска: математическое ожидание NPV и вариация NPV . Правило Марковича выбора одного из двух проектов. Модель эффективного распределения инвестиций по проектам с учетом ограничений.

В современном инвестиционном анализе денежный поток считают случайной величиной и эксперты прогнозируют распределение вероятности этой случайной величины. Тогда проект характеризуется мат ожиданием NPV, а его риск – вариацией NPV.

Xt, t=1,n – случайная величина, выражающая значение денежного потока в периоде t (n – число периодов реализ проекта).

Для простоты предполагается, что Xt – дискретная СВ. Пусть установлено, что эта СВ принимает значения: Xt1 с вероятностью pt1 и т.д.

Тогда мат ожидание NPV проекта: E(NPV)=∑𝐸(𝑋𝑡)(1+𝑟)𝑡𝑛𝑡=1−𝐼0 𝐸(𝑋𝑡)= ∑X𝑡𝑗*𝑝𝑡𝑗*𝑚𝑗=1

Риск проекта:

а) Если денежные потоки являются независимыми СВ, то вариация NPV:

V(NPV)=∑𝑉(𝑋𝑡)(1+𝑟)2𝑡𝑛𝑡=1

б) 𝑉(𝑋𝑡)=∑𝑝𝑡𝑗*𝑚𝑗=1(𝑥𝑡𝑗−𝐸(𝑋𝑡))2

в) Если ден потоки являются зависимыми СВ: V(NPV)=∑𝑉(𝑥𝑡)(1+𝑟)2𝑡𝑛𝑡=1 + ∑𝑛𝑡=1∑𝑐𝑜𝑣(𝑋𝑡𝑋𝜏)(1+𝑟)𝑡(1+𝑟)𝜏𝑛𝜏=1

Правило Марковица: Из 2-ух проектов А и Б следует выбрать А, если мат ожидание NPV проекта А не меньше, чем мат ожидание проекта Б, а риск проекта А меньше, чем риск проекта Б.

Если ни одно из условий не выполнено, то составляется соотношение ожидаемой доходности к риску и выбирают проект с большим значением этого отношения.

Пусть инвестор рассматривает m инвестиционных проектов одинаковой продолжительности. Каждый из проектов требует первоначальных инвестиций I0i и имеет чистую текущую стоимость NPV, i=1,m. Инвестиционные возможности инвестора ограничиваются суммой I0. Кроме финансовых, инвестиционные проекты требуют и других ресурсов, объём которых ограничен. Обозначим через aij – кол-во ресурса i-ого вида, необходимого для проекта j (i=1,k; j=1,m), а через a0i – общий объём ресурса вида i, имеющегося в наличии. Необходимо выбрать проекты таким образом, чтобы уложиться в имеющиеся ресурсы и чтобы сумма чистой текущей стоимости проекта была максимальной.

Математическая модель задачи: Пусть переменная xj (j>1,m) описывает j-ый проект, определим её след образом: xj={1,если инвестор выбирает 𝑗 проект;0,если инвестор отвергает 𝑗 проект. Тогда функция, выражающая суммарную чистой текущей с/с проектов будет иметь вид: 𝑓(𝑥̅)=∑𝑁𝑃𝑉𝑗𝑥𝑗𝑚𝑗=1

Ограничения по первоначальным инвестициям: ∑𝐼0𝑗𝑥𝑗𝑚𝑗=1≤𝐼0

И по другим ресурсам: ∑𝑎𝑖𝑗𝑥𝑗𝑚𝑗=1≤𝑎0𝑖,𝑖=1,𝑘̅

В итоге модель оптимального выбора инвестиционных проектов с учётом доп. ограничений:{𝑓(𝑥̅)=∑𝑁𝑃𝑉𝑗𝑥𝑗𝑚𝑗=1(𝑚𝑎𝑥)∑𝐼0𝑗𝑥𝑗𝑚𝑗=1≤𝐼0∑𝑎𝑖𝑗𝑥𝑗𝑚𝑗=1≤𝑎0𝑖,𝑖=1,𝑘̅𝑥𝑗=0∪1,𝑗=1,𝑚̅.Если проекты взаимосвязаны друг с другом, то из 2-ух проектов м.б. выбран только 1. Это условие описывается неравенством: 𝑥𝑗1+𝑥𝑗2≤1

Пусть проект j1 м.б. принят лишь в том случае когда будет принят проект j2: 𝑥𝑗1≤𝑥𝑗2.

Из 2-ух проектов д.б. принят хотя бы 1: 𝑥𝑗1+𝑥𝑗2≥1