35. Экономические примеры двойственных задач: задача об оптимальном планировании производства и задача об оценках на используемые в производстве ресурсы.

Сформулируем двойственную задачу для задачи об оптимальном планировании производства.

Условие: Предприятие выпускает четыре вида продукции П1, П2, П3 и П4. Для производства продукции оно располагает тремя ресурсами, запасы которых ограничены величинами 35, 30 и 40 единиц. Цена единицы готовой продукции соответственно равна 14, 10, 14 и 11 ден.ед. Удельные затраты на единицу продукции и цена единицы готовой продукции заданы в виде таблицы:

Удельные затраты на единицу продукции

ресурсы	Расход ресурсов на единицу продукции
	П1	П2	П3	П4
Р1	4	2	2	3
Р2	1	1	2	3
Р3	3	1	2	1

Предположим, что некоторая организация может закупить все ресурсы, которыми располагает предприятие. Необходимо определить оптимальные оценки на эти ресурсы, исходя из условия, что покупающая организация стремится минимизировать общую оценку ресурсов. Нужно учитывать тот факт, что за ресурсы покупающая организация должна уплатить сумму, не меньшую той, которую может, выручить предприятие при организации собственного производства продукции. Оставаясь в рамках производства в задаче необходимо установить оценки используемых в производстве ресурсов с учетом их влияния на конечный результат производства.

В итоге, модель задачи выглядит так:

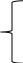φ = 35 у1 + 30 у2 + 40 у3 → min

4 у1 + у2 + 3у3 ≥ 14

2у1 + у2 + у3 ≥ 10 (3.1.23)

2у1 + 2у2 + 2у3 ≥ 14

3у1 + 3у2 + у3 ≥ 11

уi ≥ 0, i = 1,3.

Затем, с помощью необходимых преобразований находим значения двойственных переменных. Можем записать оптимальный план двойственной задачи: У = (3; 4; 0; 2; 0; 0; 10), φmin = 225.

Выводы: По оптимальному плану выпуска продукции все затраты внутри производства совпадают с оценкой готовой продукции, произведенной по этому плану, т.е. при оптимальном плане вся стоимость затрат внутри производства поглощается в стоимости готовой продукции. Т.е. затраты равны 35*3+30*4+40*0=225. Стоимость готовой продукции 14*0+10*5+14*12,5+11*0=225. Увеличение ресурса Р1 на 1 единицу привело бы к росту максимальной суммы прибыли на 3 ден.ед. (y1=3), а увеличение ресурса Р3 не повлияет на оптимальный план выпуска продукции и сумму прибыли. Недефицитным ресурсом является ресурс Р3 поскольку y3 = 0. Острее ощущается дефицитность ресурса Р2 (y2 = 4) − он более дефицитен, чем ресурс Р1 (y1 = 3).

36. Операция наращения и дисконтирования.

Наращение - процесс увеличения первоначальной суммы в результате начисления процентов. Экономический смысл метода наращения состоит в определении величины, которая будет или может быть получена из некоторой первоначальной суммы в результате проведения операции, т.е. метод наращения позволяет определить будущую величину (FV) текущей суммы (PV) через некоторый промежуток времени, исходя из заданной процентной ставки r. Дисконтирование - процесс нахождения величины на заданный момент времени по ее известному или предполагаемому значению в будущем. В экономическом смысле величина PV, найденная в процессе дисконтирования, показывает современное значение будущей величины FV. Дисконтирование - зеркальное отражение наращения. Используемую при этом процентную ставку r называют нормой дисконта. В зависимости от условий проведения финансовых операций, как наращение, так и дисконтирование, могут осуществляться с применением простых, сложных либо непрерывных процентов.

Простой %: S=P+I=P+P*r*t=P*(1+r*t). Коэф 1+r*t показывает наращенную сумму в расчете на одну денежную единицу первоначального капитала, и называется коэфом наращения. В случае простого %, коэф наращения находится: α=1+r*t, тогда S=P*α.

Сложный %: Sn=P . В случае сложного % коэф наращения a находится: α= . Эк смысл операции наращения состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции

PV = =

Коэф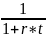 = показ текущую стоимость одной денежной ед наращенной суммы, т.е. то кол-во денег, кот нужно положить на счет в настоящий момент времени для того, чтобы обеспечить одну денежную единицу наращенной суммы. Этот коэф называют коэфом дисконтирования, т.е. PV= S*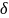

Текущая стоимость и коэф дисконтирования в случае сложного %:

PV = =

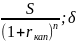Нахождение текущей стоимости суммы, выплачиваемой в будущем, называется дисконтированием. Эк смысл дисконтирования заключ во временном упорядочении денежных потоков различных временных периодов.