
- •1. Предмет экономико-математического моделирования и основные понятия и принципы моделирования социально-экономических систем.
- •2. Классификация экономико-математических моделей.
- •3. Этапы экономико-математического моделирования.
- •4. Определение эконометрической модели. Понятие регрессии и корреляции.Задачи регрессионного анализа.
- •5. Генеральная совокупность, выборка. Этапы проверки адекватности моделей.
- •6. Парная лин регрессия: спецификация модели и расчет параметров модели.
- •7. Метод наименьших квадратов.
- •8. Статистические характеристики адекватности модели.
- •9. Интерпретация параметров парной линейной регрессии.
- •10. Нелинейная регрессия и ее преобразование к линейному виду.
- •11. Множественная регрессия: спецификация модели.
- •12. Множественна регрессия: статистические характеристики адекватности.
- •13. Мультиколлинеарность факторов: обнаружение, последствия, устранение.
- •14. Стандартизованные параметры регрессии и сравнительная сила влияния факторов.
- •15. Особенности интерпретации параметров множественной регрессии.
- •16. Использование регрессионных моделей при исследовании взаимосвязей экономических показателей на пространственных данных.
- •17. Эконометрический анализ при нарушениях исходных предпосылок метода наименьших квадратов: автокорреляция остатков и критерий Дарбина - Уотсона.
- •18. Эконометрический анализ при нарушениях исходных предпосылок метода наименьших квадратов: гетероскедастичность остатков.
- •19. Понятие стационарности временных рядов.
- •20. Анализ временных рядов: аддитивная и мультипликативная модели временного ряда.
- •21. Выявление структуры временного ряда: графический метод.
- •22. Выявление структуры временного ряда на основе автокорреляционной функции уровней временного ряда.
- •23. Сезонная компонента и методы ее расчета.
- •24. Модели временных рядов с детерминированным трендом: выделение линейного тренда.
- •25. Модели вр рядов е детерминир-ным трендом: нелин формы тренда.
- •Логарифмическая:
- •Гомперца
- •26. Сущность моб, предпосылки построения моб. Схема моб.
- •27. Модель моб и взаимосвязь элементов матрицы моб
- •28. Продуктивность матрицы коэффициентов прямых затрат.
- •29. Экономическая сущность коэффициентов прямых и полных материальных затрат и их свойства.
- •31. Коэффициенты косвенных затрат и их сущность.
- •32. Использование модели моб в прогнозировании.
- •33. Принцип оптимальности в экономике и его комплексное выражение.
- •35. Экономические примеры двойственных задач: задача об оптимальном планировании производства и задача об оценках на используемые в производстве ресурсы.
- •36. Операция наращения и дисконтирования.
- •37. Основные показатели эффективности инвестиционных проектов:
- •39. Основные виды систем: управления запасами: системы с оперативным и периодическим контролем.
- •40. Простейшая модель управления запасами. Формула Уилсона.
- •41. Статистическая детерминированная модель управления запасами без дефицита
- •42. Статистическая детерминированная модель управления запасами с дефицитом
- •43. Основные понятия и определения сетевого планирования и управления.
- •44. Основные принципы построения сетевой модели.
- •45. Линейный график комплекса работ (график Ганта). Диаграмма потребления ресурсов.
- •46. Расчет временных параметров событий. Критический путь.
- •47. Сроки начала и окончания работ. Резервы времени работ.
- •Определение теории игр, основные понятия, классификация игр.
- •49. Матричные игры с нулевой суммой и их решения.
- •50.Определение оптимальной стратегии в условиях неопределенности по критериям Вальда, Сэвиджа, Гурвица.
- •51.Определение оптимальной стратегии в условиях риска по критерии Байеса.
- •52. Решение матричных игр в смешанных стратегиях
- •53. Выбор оптимального игрового решения при непредсказуемом поведении противника.
- •54. Основные понятия и примеры задач массового обслуживания.
- •55. Граф состояний, размеченный граф состояний смо.
- •56. Потоки событий. Простейший поток и его свойства
- •57. Многоканальная смо с огранич-й очередью и ее характеристики.
- •58. Многоканальная смо с неограниченной очередью и ее хар-ки.
- •59. Многоканальная смо с отказами и ее характеристики.
- •60. Одноканальная смо с ограниченной очередью и ее характеристики.
- •62. Одноканальная смо с отказами и ее характеристики.
21. Выявление структуры временного ряда: графический метод.
Основная задача эконометрического исследования отдельного временного ряда – выявление количественного выражения каждой из компонент и использование полученной информации для прогноза будущих значений ряда или построение модели взаимосвязи двух или более временных рядов.
Табличное представление временного ряда и описательные статистики чаще всего не позволяют понять характер процесса, в то время как по графику временного ряда можно сделать довольно много выводов. В дальнейшем они могут быть проверены и уточнены с помощью расчетов.
При анализе графиков можно достаточно уверенно определить:
· наличие тренда и его характер;
· наличие сезонных и циклических компонент;
· степень плавности или прерывистости изменений последовательных значений ряда после устранения тренда. По этому показателю можно судить о характере и величине корреляции между соседними элементами ряда.
По графику временного ряда можно судить о положительной (возрастающей) либо отрицательной тенденции уровней ряда, а также о наличии сезонных колебаний некоторой периодичностью.
22. Выявление структуры временного ряда на основе автокорреляционной функции уровней временного ряда.
Одним из способов выявления структуры ряда (т. е. состава компонент) является построение автокорреляционной функции – последовательности коэфов автокорреляции уровней первого, второго и др порядков.
Автокорреляция уровней ряда – корреляционная между последовательными уровнями одного и того же ряда динамики (сдвинутыми на определенный промежуток времени L – лаг). То есть связь между рядом: Х1, Х2, .... Хn-L и рядом Х1+L, Х2+L, .... Хn, где L – положительное целое число. Автокорреляция может быть измерена коэффициентов автокорреляции:
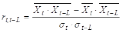 ,
Где
,
Где 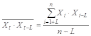 ;
;
 –
средний уровень ряда (Х1+L,
Х2+L,
.... Хn);
–
средний уровень ряда (Х1+L,
Х2+L,
.... Хn);
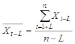 –
средний
уровень ряда (Х1,
Х2,
.... Хn-L).
–
средний
уровень ряда (Х1,
Х2,
.... Хn-L).
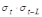 –
средние
квадратические отклонения, для рядов
(Х1+L,
Х2+L,
.... Хn)
и
(Х1,
Х2,
.... Хn-L)
соответственно.
–
средние
квадратические отклонения, для рядов
(Х1+L,
Х2+L,
.... Хn)
и
(Х1,
Х2,
.... Хn-L)
соответственно.
Лаг (сдвиг во времени) определяет порядок коэффициента автокорреляции. Если L = 1, то имеем коэффициент автокорреляции 1-го порядка rt,t-1, если L = 2, то коэффициент автокорреляции 2-го порядка rt,t-2 и т.д. Следует учитывать, что с увеличением лага на единицу число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается на 1. Поэтому обычно рекомендуют максимальный порядок коэффициента автокорреляции, равный n/4.
Рассчитав несколько коэффициентов автокорреляции, можно определить лаг (I), при котором автокорреляция (rt,t-L ) наиболее высокая, выявив тем самым структуру временного ряда. Если наиболее высоким оказывается значение rt,t-1 , то исследуемый ряд додержит только тенденцию. Если наиболее высоким оказался rt,t-L , то ряд содержит (помимо тенденции) колебания периодом L. Если ни один из rt,t-l (l=1;L) не является значимым, можно сделать одно из двух предположений:
• либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;
• либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.
Последовательность коэффициентов автокорреляции 1, 2 и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости значений коэффициентов автокорреляции от величины лага (порядка коэффициента автокорреляции) называют коррелограммой.
