19. Понятие стационарности временных рядов.

Поиск модели, адекватно описывающей поведение случайной компоненты   анализируемого временного ряда   , осуществляется, как правило, в рамках специального класса – класса стационарных временных рядов. Под стационарностью временного ряда понимают неизменность вероятностных свойств членов ряда во времени.

Статистический процесс называется строго стационарным, если взаимное распределение вероятностей m наблюдений инвариантно по отношению к общему сдвигу временного аргумента, т.е. совместная плотность распределения случайных величин x_t1 , x_t2 , . . . , x_tm такая же, как для величин x_t1+k, x_t2+k, . . . , x_tm+k при любых целых значениях сдвига k . Когда m = 1 , из предположения стационарности следует, что безусловное распределение величины x(t) , p(xt) , одиаково для всех t и может быть записано как p(x) .

Требование стационарности, определенное этими условиями, является достаточно жестким. На практике при изучении случайных процессов ограничиваются моментами первого и второго порядка, и тогда говорят о слабой стационарности или стационарности второго порядка. В этом случае процесс имеет постоянное среднее значение µ = E(x_t) для всех t, определяющее уровень, относительно которого он флуктуирует, постоянную дисперсию σ² =E(x_t−µ)² для всех t и постоянную автоковариацию γ_k = E(x_t−µ)(x_t+k −µ) для всех t , т.е. ковариация между x_t и x_t+k зависит только от величины сдвига k и не зависит от t.(Следует иметь в виду, что два процесса, имеющие одинаковые моменты первого и второго порядка, могут иметь разный характер распределения.)

Понятно, что согласно данным определениям стационарным может быть только бесконечно длящийся процесс, но не конечный временной ряд x₁, . . . , x_T .

Однако мы можем называть временной ряд x₁, . . . , x_T стационарным, если он может быть частью бесконечного стационарного процесса {x_t}_t=−∞,... ,+∞ .

Среди стационарных процессов в теории временных рядов особую роль играют процессы типа «белый шум». Это неавтокоррелированные слабо стационарные процессы с нулевым математическим ожиданием. Таким образом, процесс { ε_t } является «белым шумом», если

µ = E(ε_t) = 0,

γ₀ = E(ε_2t ) = σ²,

γ_k = E(ε_t, ε_t−k) = 0, ∀k ≠ 0

20. Анализ временных рядов: аддитивная и мультипликативная модели временного ряда.

Каждый уровень временного ряды формируется под воздействием большого числа факторов, которые можно разделить на 3 группы:

Длительные, постоянно действующие факторы, оказывающие на изучаемое явление определяющее влияние и формирующие основную тенденцию ряда – тренд T(t).

Кратковременные периодические факторы, формирующие сезонные колебания ряда S(t).

Случайны факторы, которые формируют случайные изменения уровней ряда ε(t).

Аддитивной моделью временного ряда называется модель, в которой каждый уровень ряда представлен суммой тренда, сезонной и случайной компоненты:

.

Мультипликативная модель – это модель, в которой каждый уровень ряда представляет собой произведение перечисленных компонент:

.

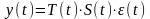Выбор одной из моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний примерно постоянна, то строят аддитивную модель. Если амплитуда возрастает, то мультипликативную модель.

Основная задача эконометрического анализа заключается в выявлении каждой из перечисленных компонент.

Процесс построения модели включает в себя следующие шаги.

1.       Выравнивание исходного ряда методом скользящей средней.

2.      Расчет значений сезонной компоненты.

3.      Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной или мультипликативной модели.

4.      Аналитическое выравнивание уровней и расчет значений тренда с использованием полученного уравнения тренда.

5.      Расчет полученных по модели значений или

6.      Расчет абсолютных и относительных ошибок.

Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок для анализа взаимосвязи исходного ряда и других временных рядов.