15. Особенности интерпретации параметров множественной регрессии.

Регрессионные коэффициенты (или B-коэффициенты) представляют независимые вклады каждой независимой переменной в предсказание зависимой переменной. Другими словами, переменная X1, к примеру, коррелирует с переменной Y после учета влияния всех других независимых переменных. Этот тип корреляции упоминается также под названием частной корреляции

R² в случае множественной регрессии указывает на то, что рассматривается вариабельность всей совокупности факторов, введенных в множественную линейную регрессию. Иначе говоря, интерпретация коэффициента множественной детерминации (R2) аналогична коэффициенту детерминации для простой линейной регрессии и указывает какая часть общей дисперсии может быть объяснена зависимостью y от совокупности факторов. В множественной регрессии дополнительно также могут рассчитываться коэффициенты частной детерминации, которые характеризуют связь зависимого показателя и отдельных факторов при фиксировании или исключении влияния остальных факторов.

Однако, в отличие от аналогичных характеристик однофакторной регрессии, особенности множественной регрессии состоят: во-первых, в возможности наличия мультиколлинеарности факторов, включаемых в модель, что нежелательно в силу ненадежности оценок параметров регрес-сии; во-вторых, в возможности расчета стандартизованных коэффициентов регрессии и частных коэффициентов корреляции и детерминации, которые позволяют оценивать сравнительную силу влияния факторов; в-третьих, в некотором изменении экономической интерпретации параметров регрессии. Далее более подробно остановимся на этих отличиях.

В многофакторной регрессии добавление дополнительных объясняющих переменных увеличивает коэффициент детерминации. Следовательно, коэффициент детерминации должен быть скорректирован с учетом числа независимых переменных.

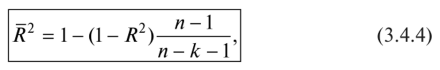
СМОТРИ ЕЩЕ ВОПРОС 12.

16. Использование регрессионных моделей при исследовании взаимосвязей экономических показателей на пространственных данных.

Пространственными данными называется совокупность экономической информации, которая характеризует различные объекты, однако полученной за один и тот же период или момент времени.

Пространственные данные являются выборочной совокупностью из некоторой генеральной совокупности. Примером пространственных данных может служить комплекс экономической информации по какому-либо предприятию.

Регрессионный анализ позволяет моделировать, проверять и исследовать пространственные отношения и помогает объяснить факторы, стоящие за наблюдаемыми пространственными структурными закономерностями. При моделирование пространственных отношений, однако, регрессионный анализ также может быть пригоден для прогнозирования.

Методика разработки регрессионных моделей на пространственных данных является наиболее простой.

Процесс построения и использования регрессионных моделей включает в себя следующие основные этапы:

• постановку проблемы;

В рамках постановки проблемы сложной представляется процедура формирования набора факторов, включаемых в модель.

• получение данных, анализ их качества;

Основной базой данных для эконометрических исследований служат данные официальной статистики, либо данные бухгалтерского учета.

• спецификацию модели;

Предполагает непосредственное использование методов математической статистики и предусматривает оценку параметров модели и расчет диагностических тестов.

• интерпретацию результатов.

В этой части особое значение придается экономической интерпретации коэффициентов регрессионной модели.

Во многих случаях для анализа тех либо других экономических процессов важен порядок получения статистических данных. Но при рассмотрении пространственных данных порядок их получения не играет существенной роли.

Используя эконометрические модели, можно оценить величину зависимости, ее надежность и форму связи. Выявление статистически значимой связи между показателями способно повысить эффективность воздействия управляющих параметров на развитие экономического объекта. Например, выявление статистически значимых факторов инфляции позволяет углубить понимание природы инфляционных процессов в экономике и на этой основе выработать эффективные мероприятия антиинфляционной политики.