
Вопрос 1.
Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака.
Вариация является результатом того, что данный уровень изучаемого явления складывается под влиянием с одной стороны внутренних, необходимых причин, а с другой – внешних, случайных факторов. В итоге их взаимодействия, которое проявляется с неодинаковой силой и интенсивностью, у каждой единицы совокупности складывается тот или иной ее уровень, чаще всего отличающийся от других единиц совокупности.
Пример: средний доход:
А) нищего и миллионера: ( 0+1000000):2=500000
Б) доход 495000 и 505000 руб: (495000+505000):2=500000
- абсолютный
Размах вариации ( амплитуда) (R) – характеризует общую колеблемость признака, представляет собой разность между максимальных и минимальным значением признака :
R=Xmax-Xmin
он показывает общую колеблемость признака, но не характеризует степень интенсивности колебаний.
-средние
Средние линейные отклонения (l) – это среднее арифметическое из отклонений индивидуальных значений от средней. Оно учитывает отличие всех едениц совокупности от средней арифметической. Расчет ее, исходя из нулевого свойства средней арифметической, ведется по модулю, т.е.
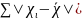
Оно всегда бывает положительной величиной, хотя индивидуальные отклонения могут быть как положительными, так и отрицательными.
Среднее линейное отклонение (l) вычисляется:
Для несгруппированных данных:
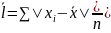
Для сгруппированных данных:
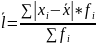
Где:
xi – середина i-го интервала или величина средней на интервале
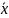 – средняя
величина
– средняя
величина
fi – частота i-го интервала
Дисперсия
(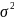 )
– это средняя величина из квадратов
отклонений вариант значений признаков
от их средней величины.
)
– это средняя величина из квадратов
отклонений вариант значений признаков
от их средней величины.
Для несгруппированных данный:
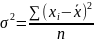
Для сгруппированных данных:
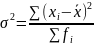
Среднее
квадратическое отклонение(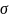 )
– это корень квадратный из дисперсии:
)
– это корень квадратный из дисперсии:
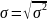
Для несгруппированных данных
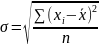
Для сгруппированных данных:
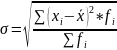
Относительные показатели вариации
Служат для характеристики меры колеблемости
Позволяют сравнивать характер рассеивания в различных распределениях:
Пр сравнении различных единиц наблюдения одного и того же признака в двух совокупностях
При различных значениях средних
При сравнении разноименных совокупностей
Коэффициент осцилляции – показывает относительную колеблемость крайних значений признаков вокруг средней.
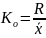
Относительное линейное отклонение(Kl) характеризует долю усредненного значения абсолютных отклонений от средней:
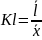
Коэффициент вариации:
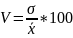
Коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин. Коэффициент вариации характеризует степень однородности совокупности. Совокупность считается однородной при V<33%.
Если V>33%, то говорят о большой колеблемости признаков в изучаемой совокупности. При этом совокупность считается неоднородной.
Группы рабочих по стажу,лет |
Количество рабочих человек,(f) |
Расчетные показатели |
|||||||
Середина интервала, (х) |
xf |
|
|
|
|
||||
6-10 |
15 |
8 |
120 |
6 |
90 |
36 |
540 |
||
10-14 |
30 |
12 |
360 |
2 |
60 |
4 |
120 |
||
14-18 |
45 |
16 |
720 |
2 |
90 |
4 |
180 |
||
18-22 |
10 |
20 |
200 |
6 |
60 |
36 |
360 |
||
Всего |
100 |
|
1400 |
Х |
300 |
Х |
1200 |
||
РАСЧЕТ ПОКАЗАТЕЛЕЙ ВАРИАЦИИ
Размах вариации: R=22-6=16 (лет)
Среднее
значение признака:
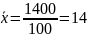 лет
лет
Среднее
линейное отклонение:
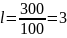 года
года
Дисперсия:
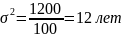
Среднее
квадратическое отклонение
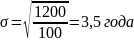
Коэффициент вариации:
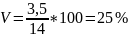
ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ СВОЙСТВА ДИСПЕРСИИ И СПОСОБЫ еЕ ВЫЧИСЛЕНИЯ
Дисперсия имеет ряд математических свойств, которые могут быть использованы для упрощения ее расчета.
Если индивидуальные значения признака уменьшить или увеличить на некоторое постоянное число, то дисперсия не изменится
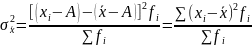
Если индивидуальные значения признака разделить или умножить на некоторое постоянное число, то дисперсия соответственно уменьшится ( увеличится) в квадрат от постоянной числа раз
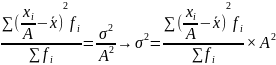
Дисперсия, рассчитанная от большей постоянной величины, больше дисперсии, рассчитанной от средней, на квадрат разности между средней величиной и постоянной
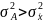
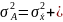
Если постоянную величину приравнять к нулю, то дисперсия будет равна разности между средним квадратом значений признака и квадратом средней:
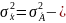
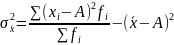
При А=0 получим:
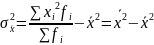
Таким образом , дисперсию можно рассчитать вторым способом:
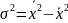
Где:
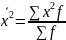

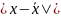
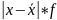
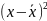
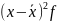
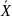 =14
=14